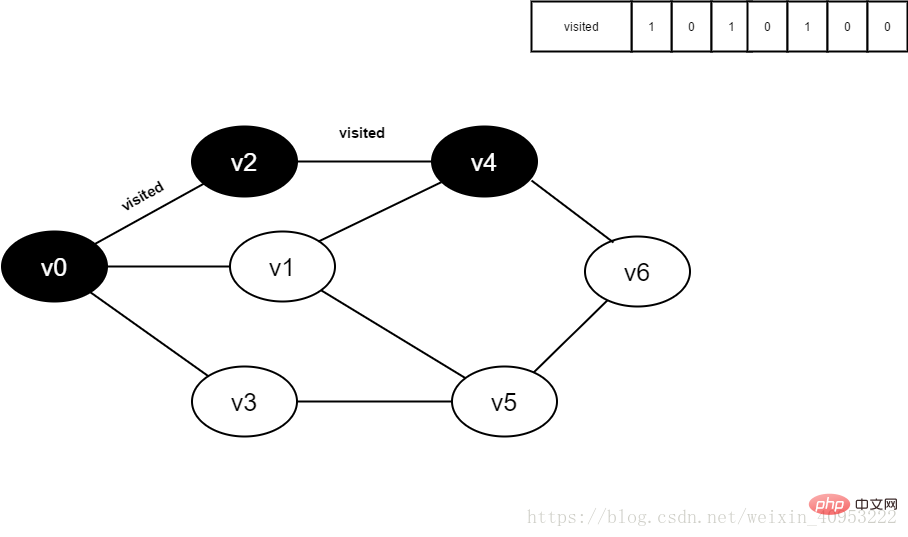
图的广度优先遍历类似于二叉树的什么?
- 青灯夜游原创
- 2020-08-29 16:44:3222663浏览
图的广度优先遍历即横向优先遍历,类似于二叉树的按层遍历。广度优先遍历是从根结点开始沿着树的宽度搜索遍历,即按层次的去遍历;从上往下对每一层依次访问,在每层中,从左往右(或右往左)访问结点,访问完一层就进入下一层,直到没有结点可以访问为止。

1.前言
和树的遍历类似,图的遍历也是从图中某点出发,然后按照某种方法对图中所有顶点进行访问,且仅访问一次。
但是图的遍历相对树而言要更为复杂。因为图中的任意顶点都可能与其他顶点相邻,所以在图的遍历中必须记录已被访问的顶点,避免重复访问。
根据搜索路径的不同,我们可以将遍历图的方法分为两种:广度优先搜索和深度优先搜索。
2.图的基本概念
2.1.无向图和无向图
顶点对(u,v)是无序的,即(u,v)和(v,u)是同一条边。常用一对圆括号表示。
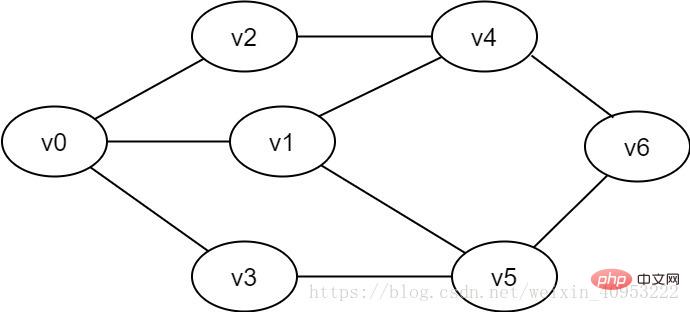
图2-1-1 无向图示例
顶点对
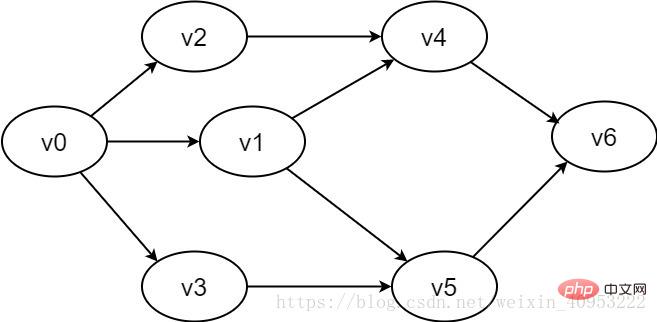
图2-1-2 有向图示例
2.2.权和网
图的每条边上可能存在具有某种含义的数值,称该数值为该边上的权。而这种带权的图被称为网。
2.3.连通图与非连通图
连通图:在无向图G中,从顶点v到顶点v'有路径,则称v和v'是联通的。若图中任意两顶点v、v'∈V,v和v'之间均联通,则称G是连通图。上述两图均为连通图。
非连通图:若无向图G中,存在v和v'之间不连通,则称G是非连通图。
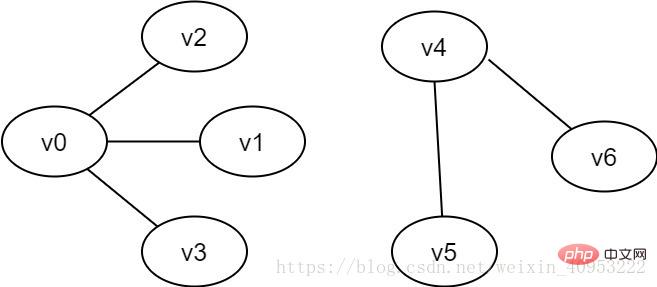
图2-3 非连通图示例
3.广度优先搜索
3.1.算法的基本思路
广度优先搜索类似于树的层次遍历过程。它需要借助一个队列来实现。如图2-1-1所示,要想遍历从v0到v6的每一个顶点,我们可以设v0为第一层,v1、v2、v3为第二层,v4、v5为第三层,v6为第四层,再逐个遍历每一层的每个顶点。
具体过程如下:
1.准备工作:创建一个visited数组,用来记录已被访问过的顶点;创建一个队列,用来存放每一层的顶点;初始化图G。
2.从图中的v0开始访问,将的visited[v0]数组的值设置为true,同时将v0入队。
3.只要队列不空,则重复如下操作:
(1)队头顶点u出队。
(2)依次检查u的所有邻接顶点w,若visited[w]的值为false,则访问w,并将visited[w]置为true,同时将w入队。
3.2.算法的实现过程
白色表示未被访问,灰色表示即将访问,黑色表示已访问。
visited数组:0表示未访问,1表示以访问。
队列:队头出元素,队尾进元素。
1.初始时全部顶点均未被访问,visited数组初始化为0,队列中没有元素。
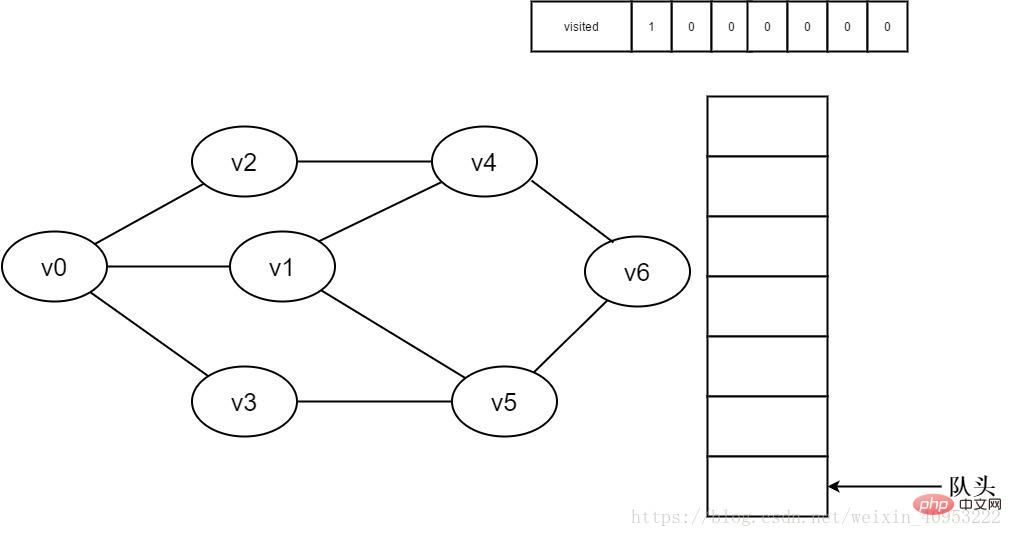
图3-2-1
2.即将访问顶点v0。
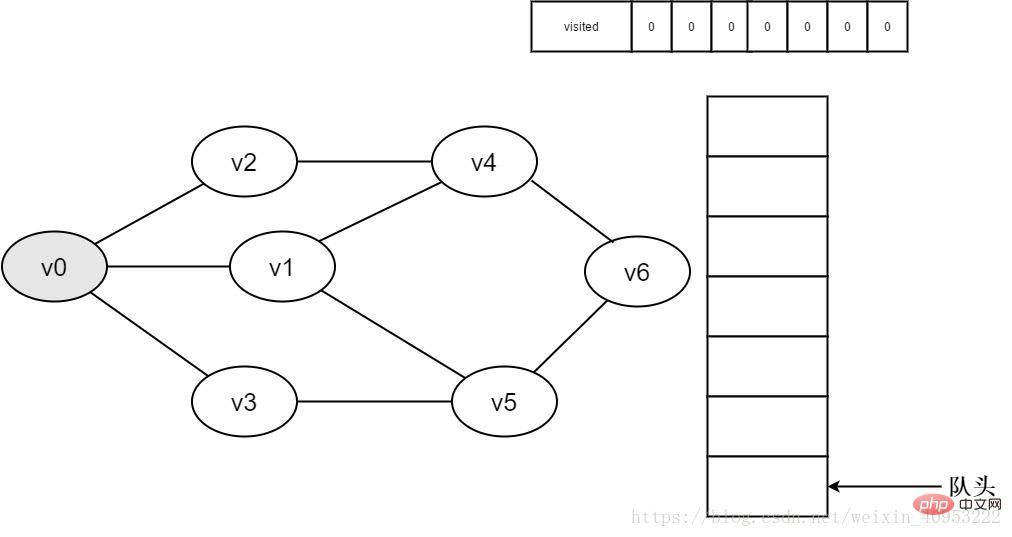
图3-2-2
3.访问顶点v0,并置visited[0]的值为1,同时将v0入队。
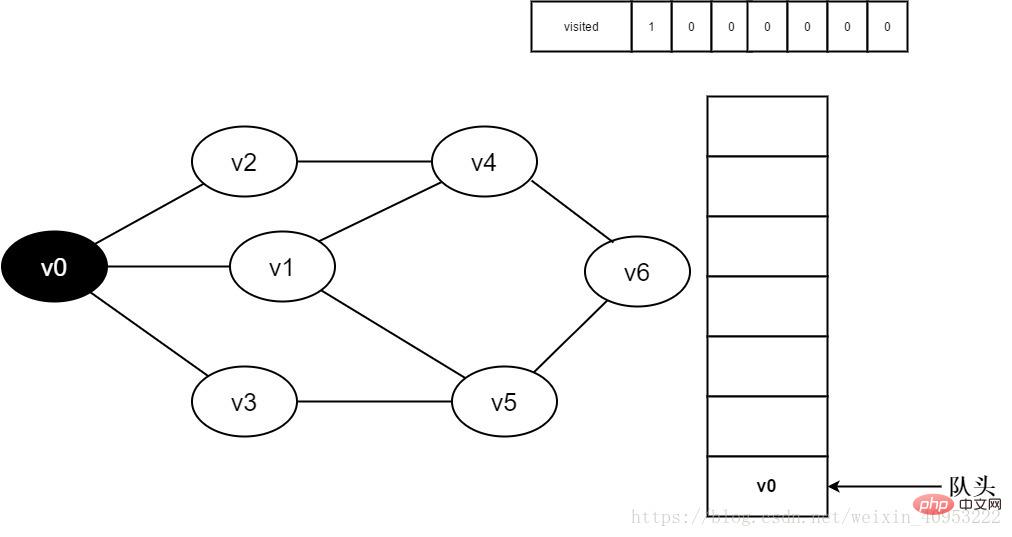
图3-2-3
4.将v0出队,访问v0的邻接点v2。判断visited[2],因为visited[2]的值为0,访问v2。
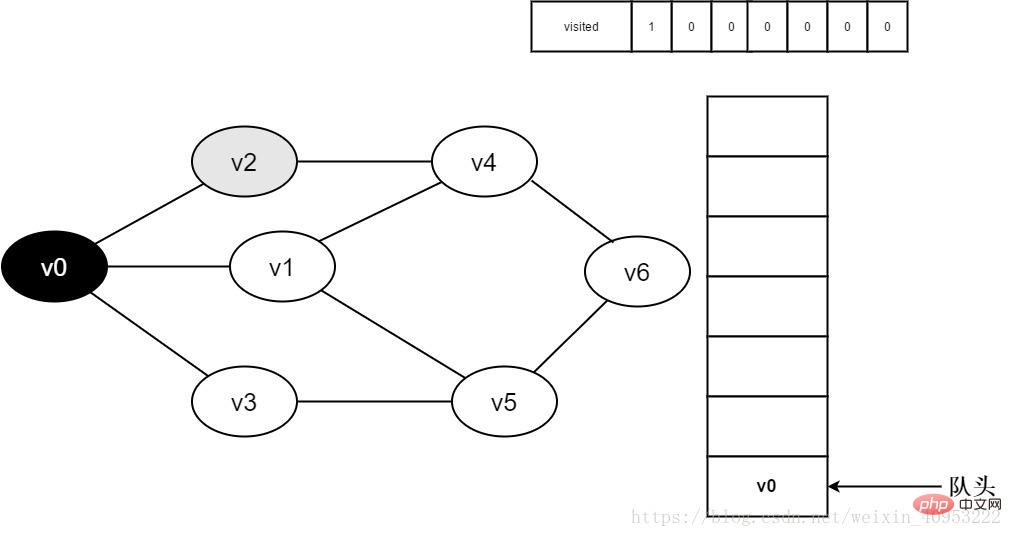
图3-2-4
5.将visited[2]置为1,并将v2入队。
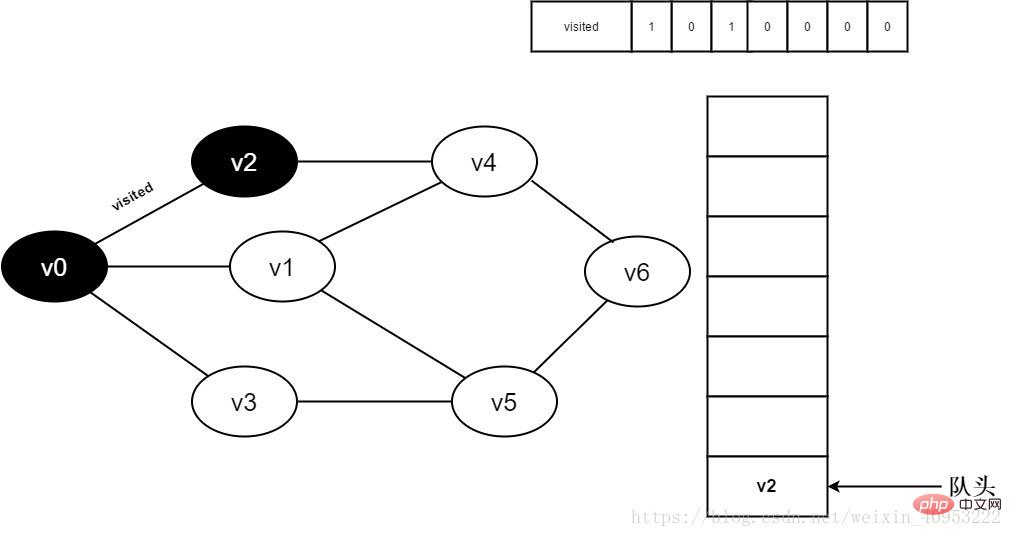
图3-2-5
6.访问v0邻接点v1。判断visited[1],因为visited[1]的值为0,访问v1。
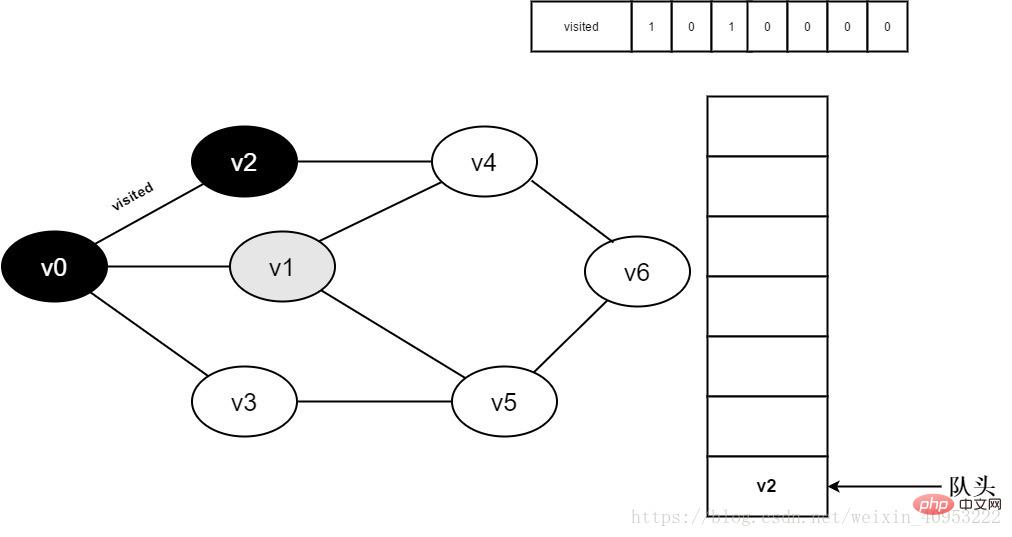
图3-2-6
7.将visited[1]置为0,并将v1入队。
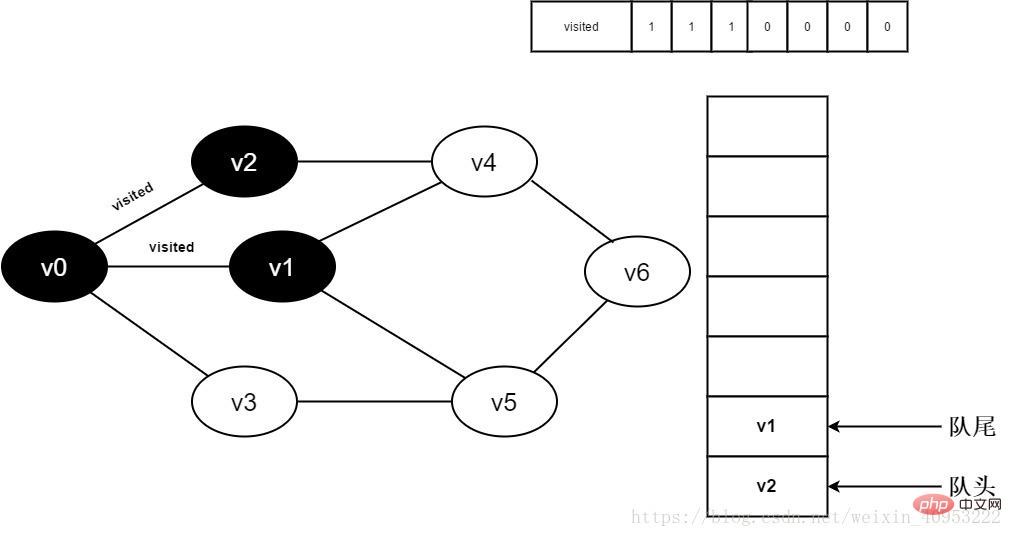
图3-2-7
8.判断visited[3],因为它的值为0,访问v3。将visited[3]置为0,并将v3入队。
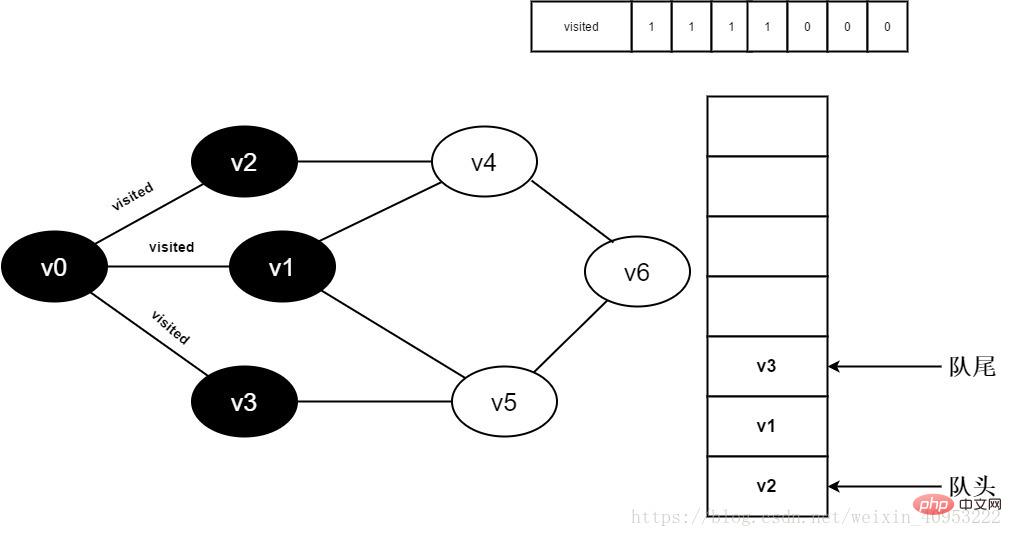
图3-2-8
9.v0的全部邻接点均已被访问完毕。将队头元素v2出队,开始访问v2的所有邻接点。
开始访问v2邻接点v0,判断visited[0],因为其值为1,不进行访问。
继续访问v2邻接点v4,判断visited[4],因为其值为0,访问v4,如下图:
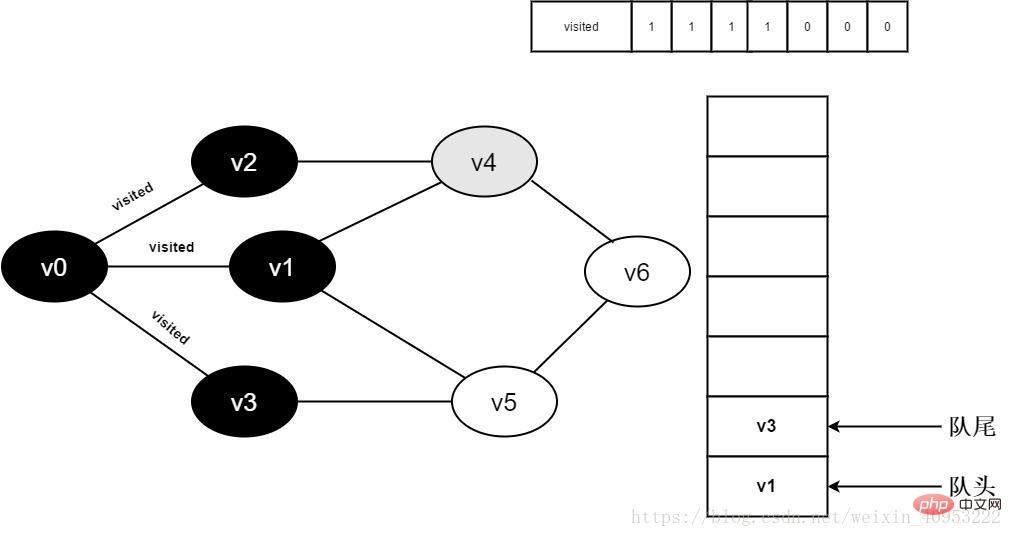
图3-2-9
10.将visited[4]置为1,并将v4入队。

图3-2-10
11.v2的全部邻接点均已被访问完毕。将队头元素v1出队,开始访问v1的所有邻接点。
开始访问v1邻接点v0,因为visited[0]值为1,不进行访问。
继续访问v1邻接点v4,因为visited[4]的值为1,不进行访问。
继续访问v1邻接点v5,因为visited[5]值为0,访问v5,如下图:

图3-2-11
12.将visited[5]置为1,并将v5入队。
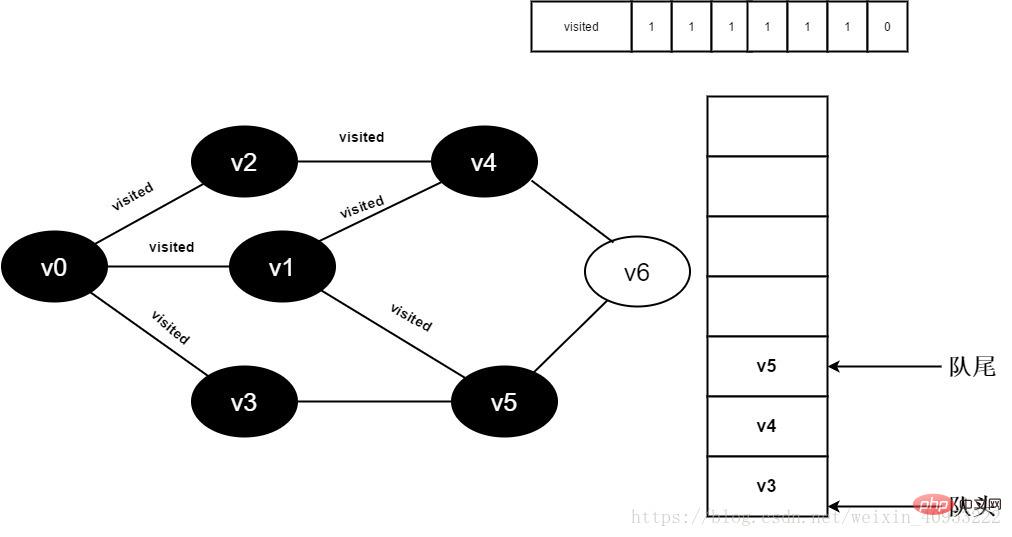
图3-2-12
13.v1的全部邻接点均已被访问完毕,将队头元素v3出队,开始访问v3的所有邻接点。
开始访问v3邻接点v0,因为visited[0]值为1,不进行访问。
继续访问v3邻接点v5,因为visited[5]值为1,不进行访问。
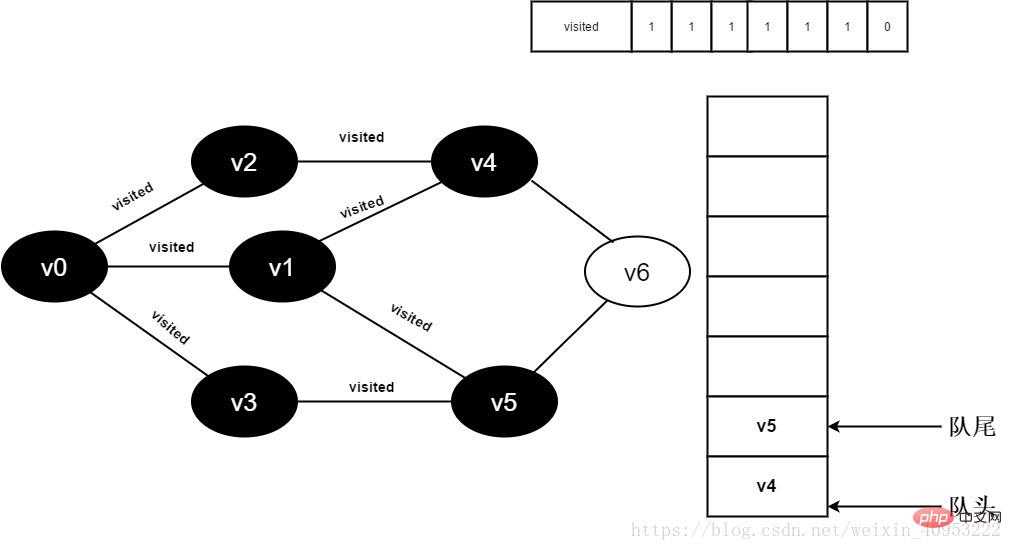
图3-2-13
14.v3的全部邻接点均已被访问完毕,将队头元素v4出队,开始访问v4的所有邻接点。
开始访问v4的邻接点v2,因为visited[2]的值为1,不进行访问。
继续访问v4的邻接点v6,因为visited[6]的值为0,访问v6,如下图:
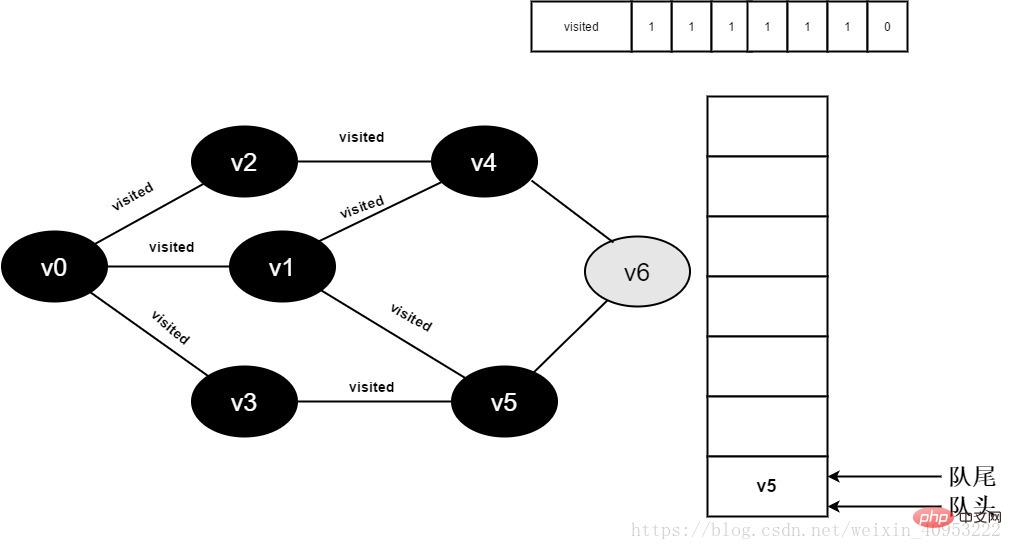
图3-2-14
15.将visited[6]值为1,并将v6入队。
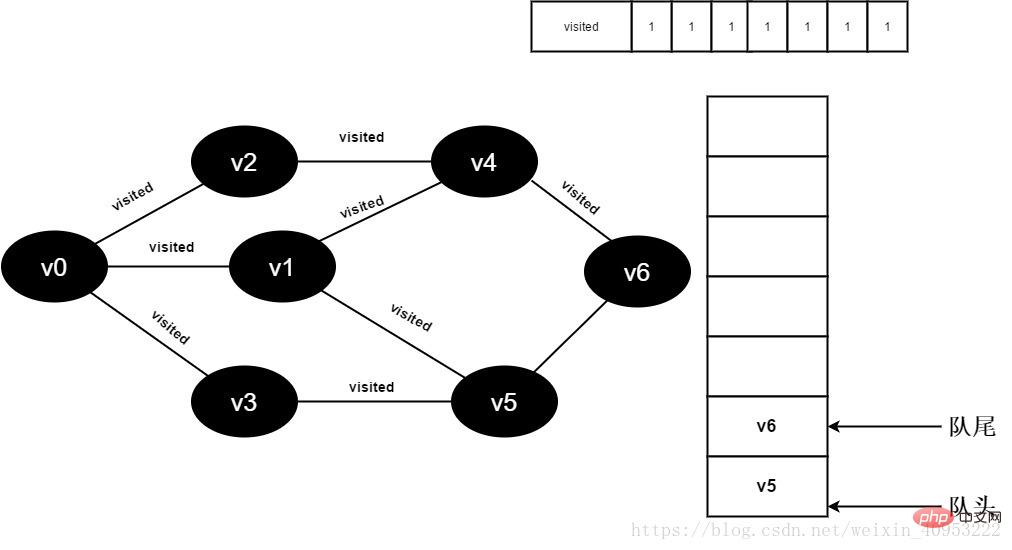
图3-2-15
16.v4的全部邻接点均已被访问完毕,将队头元素v5出队,开始访问v5的所有邻接点。
开始访问v5邻接点v3,因为visited[3]的值为1,不进行访问。
继续访问v5邻接点v6,因为visited[6]的值为1,不进行访问。
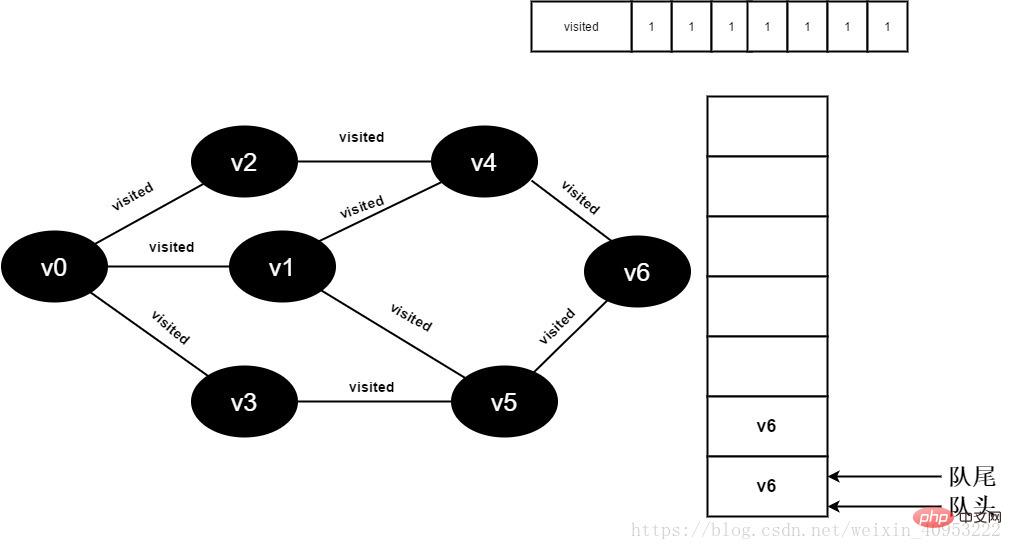
图3-2-16
17.v5的全部邻接点均已被访问完毕,将队头元素v6出队,开始访问v6的所有邻接点。
开始访问v6邻接点v4,因为visited[4]的值为1,不进行访问。
继续访问v6邻接点v5,因为visited[5]的值文1,不进行访问。
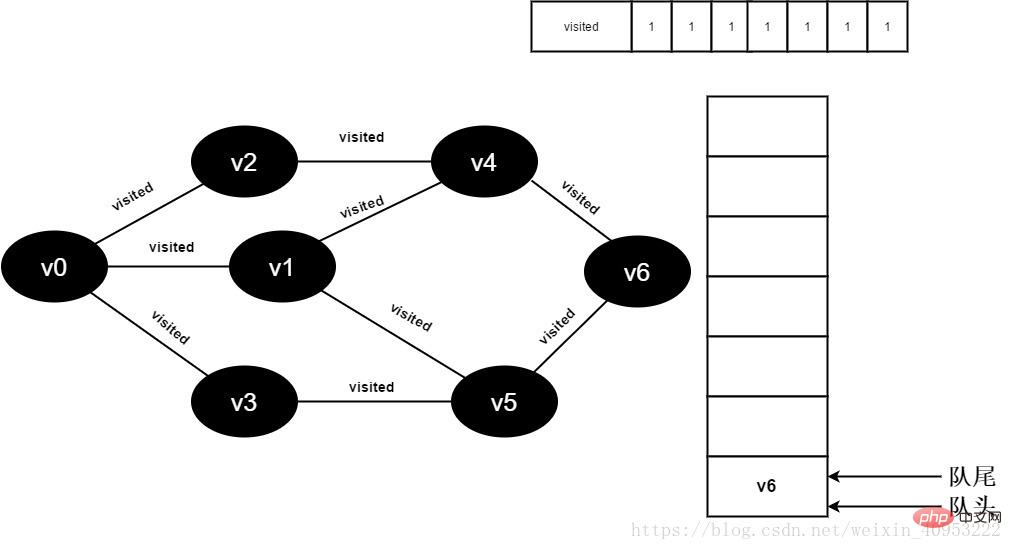
图3-2-17
18.队列为空,退出循环,全部顶点均访问完毕。

图3-2-18
3.3具体代码的实现
3.3.1用邻接矩阵表示图的广度优先搜索
/*一些量的定义*/ queue<char> q; //定义一个队列,使用库函数queue #define MVNum 100 //表示最大顶点个数 bool visited[MVNum]; //定义一个visited数组,记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;
/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法,创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar(); //获取'\n’,防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边,0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边,无向图不区分方向
}
return 1;
}/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}3.3.2用邻接表表示图的广度优先搜索
/*找到顶点对应的下标*/
int LocateVex(ALGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (v == G.vertices[i].data)
return i;
}/*邻接表存储表示*/
typedef struct ArcNode //边结点
{
int adjvex; //该边所指向的顶点的位置
ArcNode *nextarc; //指向下一条边的指针
int info; //和边相关的信息,如权值
}ArcNode;
typedef struct VexNode //表头结点
{
char data;
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VexNode,AdjList[MVNum]; //AbjList表示一个表头结点表
typedef struct ALGraph
{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;/*采用邻接表表示法,创建无向图G*/
int CreateUDG_2(ALGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar();
for (i = 0; i < G.vexnum; i++) //输入各顶点,构造表头结点表
{
scanf("%c", &G.vertices[i].data); //输入顶点值
G.vertices[i].firstarc = NULL; //初始化每个表头结点的指针域为NULL
}
for (k = 0; k < G.arcnum; k++) //输入各边,构造邻接表
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的两个顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
ArcNode *p1 = new ArcNode; //创建一个边结点*p1
p1->adjvex = j; //其邻接点域为j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; // 将新结点*p插入到顶点v1的边表头部
ArcNode *p2 = new ArcNode; //生成另一个对称的新的表结点*p2
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p1;
}
return 1;
}
/*采用邻接表表示图的广度优先遍历*/
void BFS_AL(ALGraph &G, char v0)
{
int u,w,v;
ArcNode *p;
printf("%c ", v0); //打印顶点v0
v = LocateVex(G, v0); //找到v0对应的下标
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将顶点v0入队
while (!q.empty())
{
u = q.front(); //将顶点元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍历顶点u的邻接点
{
w = p->adjvex;
if (!visited[w]) //顶点p未被访问
{
printf("%c ", G.vertices[w].data); //打印顶点p
visited[w] = 1; //顶点p已被访问
q.push(G.vertices[w].data); //将顶点p入队
}
}
}
}
3.4.非联通图的广度优先遍历的实现方法
/*广度优先搜索非连通图*/
void BFSTraverse(AMGraph G)
{
int v;
for (v = 0; v < G.vexnum; v++)
visited[v] = 0; //将visited数组初始化
for (v = 0; v < G.vexnum; v++)
if (!visited[v]) BFS_AM(G, G.vexs[v]); //对尚未访问的顶点调用BFS
}4.深度优先搜索
4.1算法的基本思路
深度优先搜索类似于树的先序遍历,具体过程如下:
准备工作:创建一个visited数组,用于记录所有被访问过的顶点。
1.从图中v0出发,访问v0。
2.找出v0的第一个未被访问的邻接点,访问该顶点。以该顶点为新顶点,重复此步骤,直至刚访问过的顶点没有未被访问的邻接点为止。
3.返回前一个访问过的仍有未被访问邻接点的顶点,继续访问该顶点的下一个未被访问领接点。
4.重复2,3步骤,直至所有顶点均被访问,搜索结束。
4.2算法的实现过程
1.初始时所有顶点均未被访问,visited数组为空。

图4-2-1
2.即将访问v0。

图4-2-2
3.访问v0,并将visited[0]的值置为1。
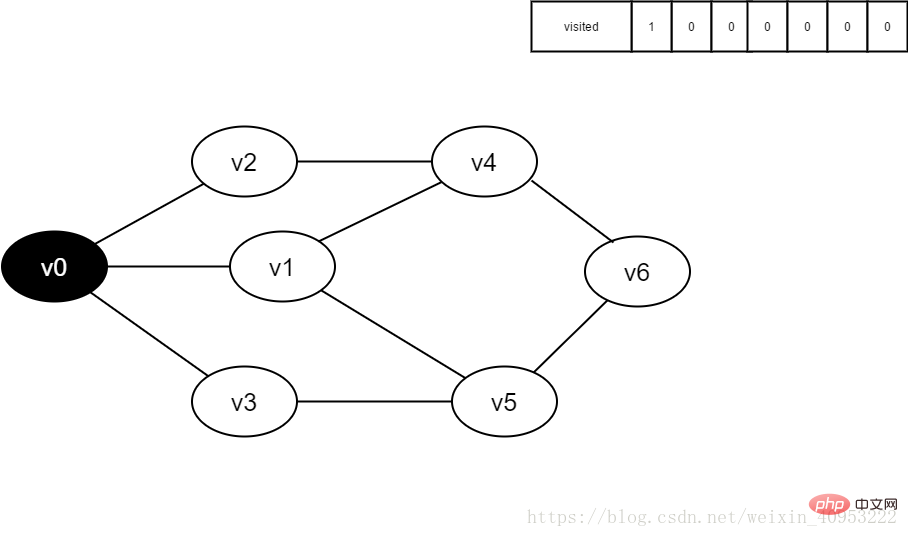
图4-2-3
4.访问v0的邻接点v2,判断visited[2],因其值为0,访问v2。
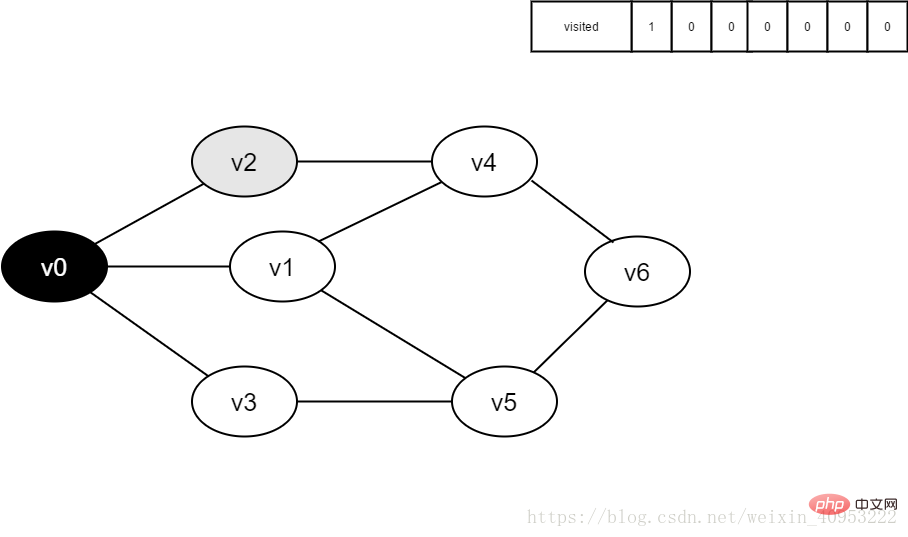
图4-2-4
5.将visited[2]置为1。
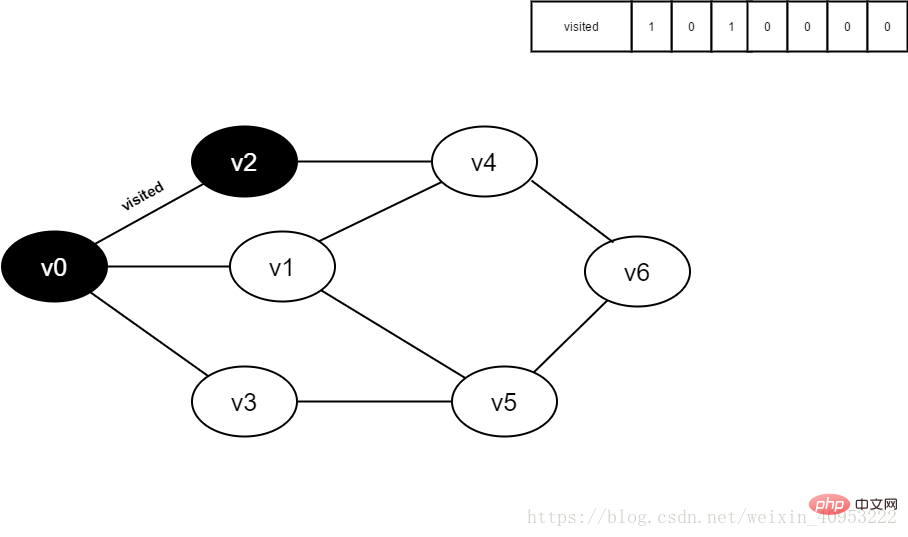
图4-2-5
6.访问v2的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v2的邻接点v4,判断visited[4],其值为0,访问v4。
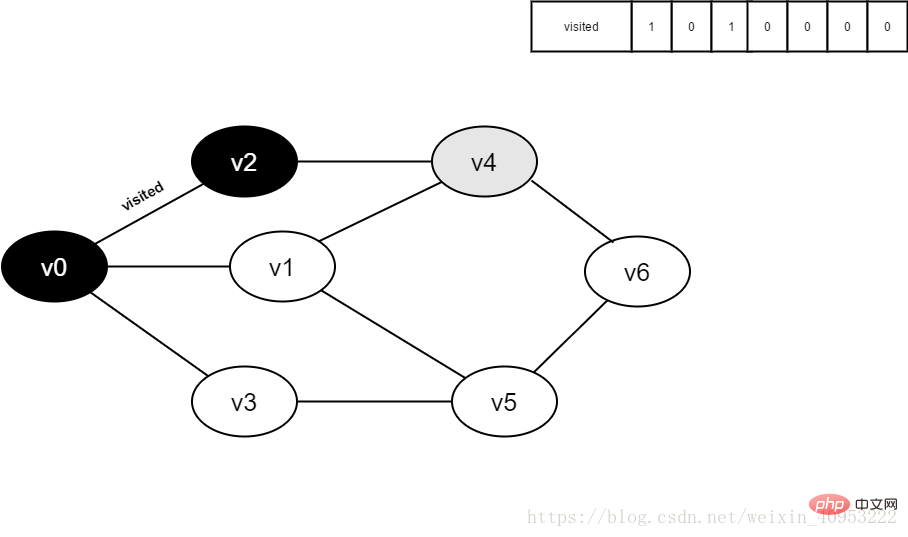
图4-2-6
7.将visited[4]置为1。
图4-2-7
8.访问v4的邻接点v1,判断visited[1],其值为0,访问v1。
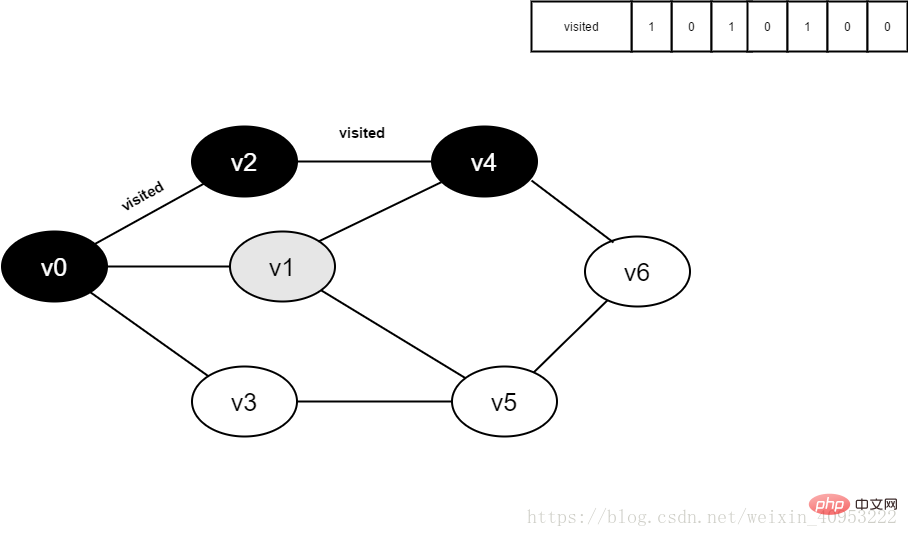
图4-2-8
9.将visited[1]置为1。
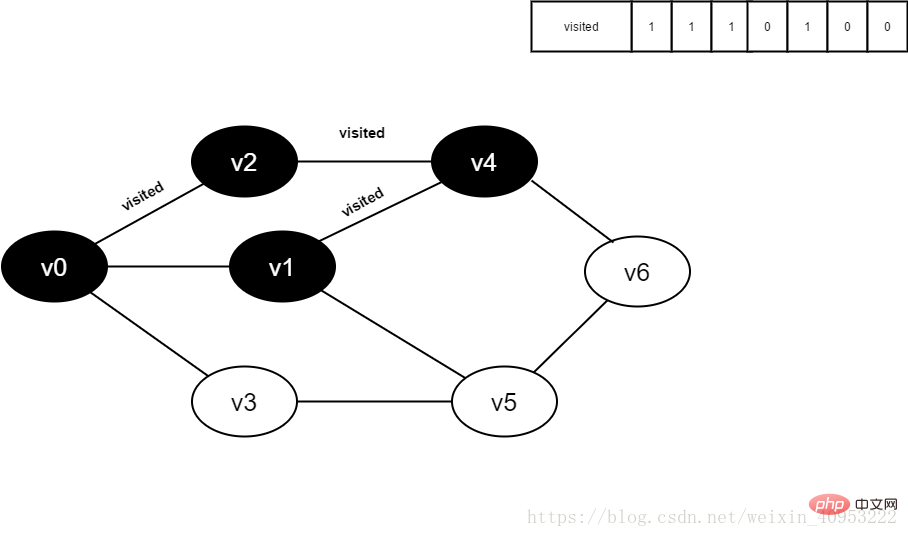
图4-2-9
10.访问v1的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v1的邻接点v4,判断visited[4],其值为1,不访问。
继续访问v1的邻接点v5,判读visited[5],其值为0,访问v5。
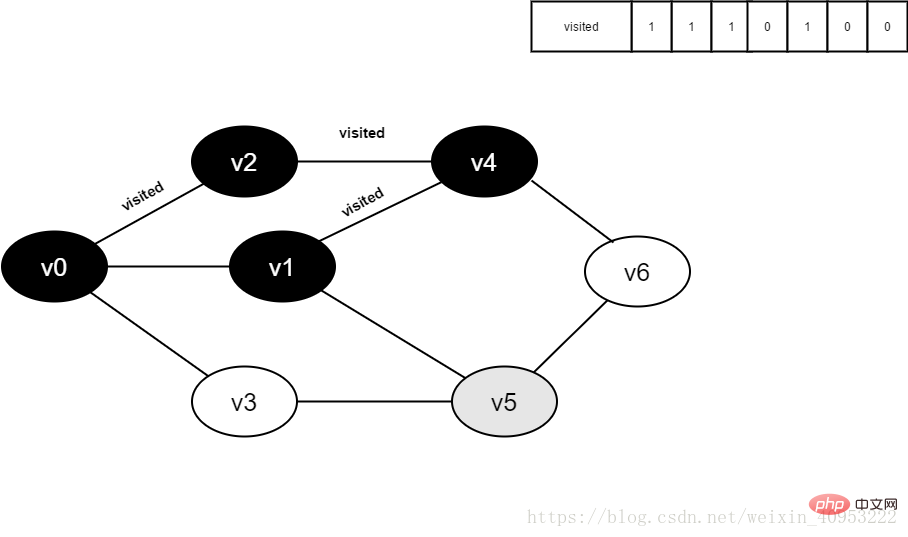
图4-2-10
11.将visited[5]置为1。
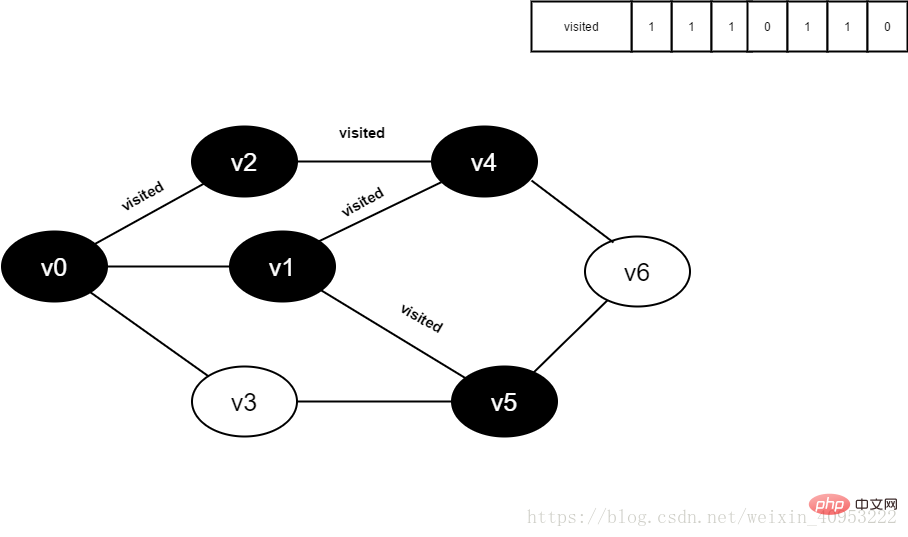
图4-2-11
12.访问v5的邻接点v1,判断visited[1],其值为1,不访问。
继续访问v5的邻接点v3,判断visited[3],其值为0,访问v3。
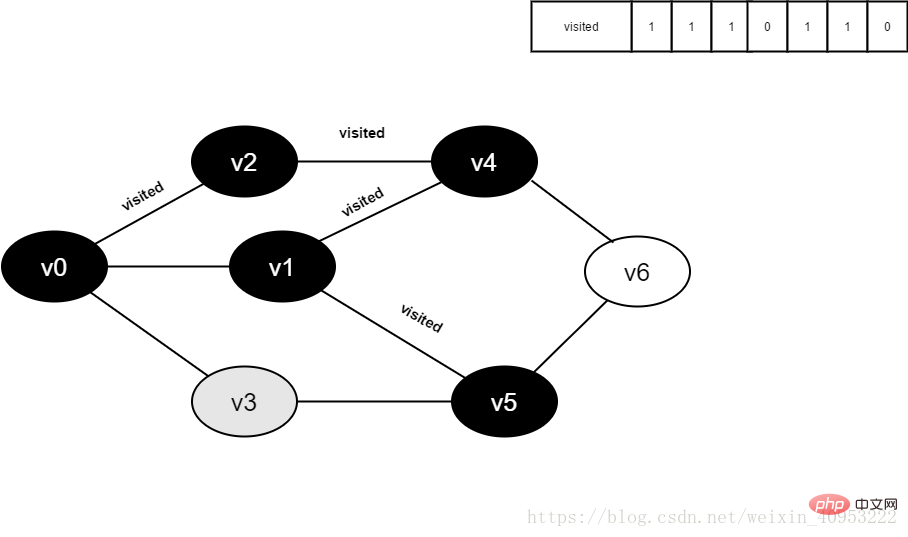
图4-2-12
13.将visited[1]置为1。
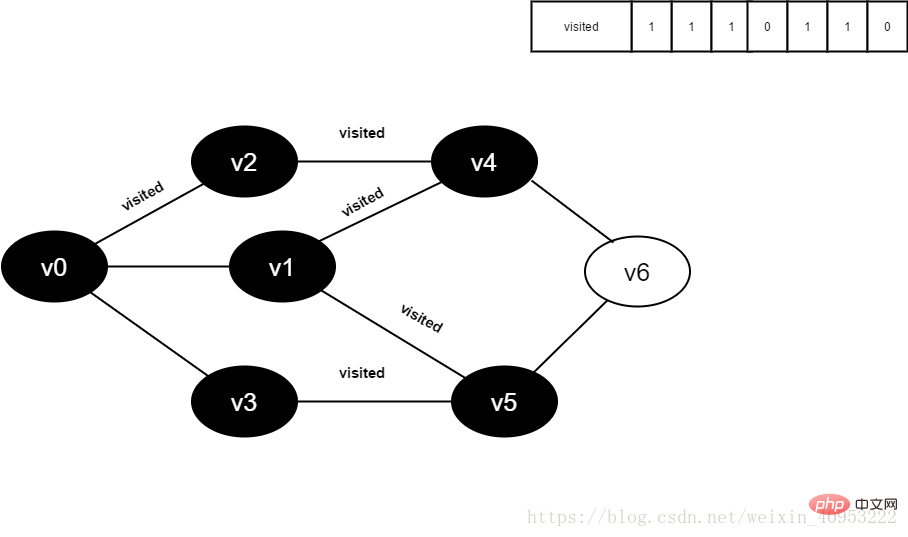
图4-2-13
14.访问v3的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v3的邻接点v5,判断visited[5],其值为1,不访问。
v3所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5所有邻接点。
访问v5的邻接点v6,判断visited[6],其值为0,访问v6。
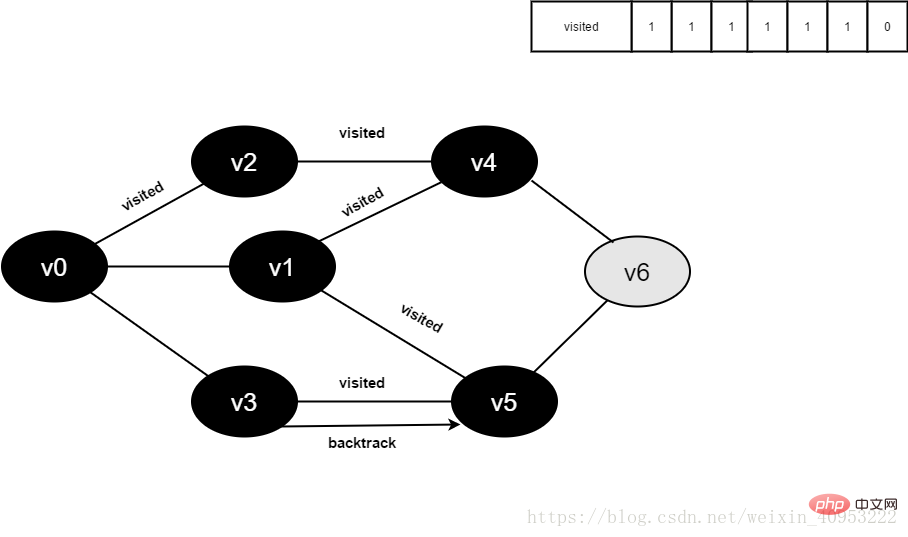
图4-2-14
15.将visited[6]置为1。
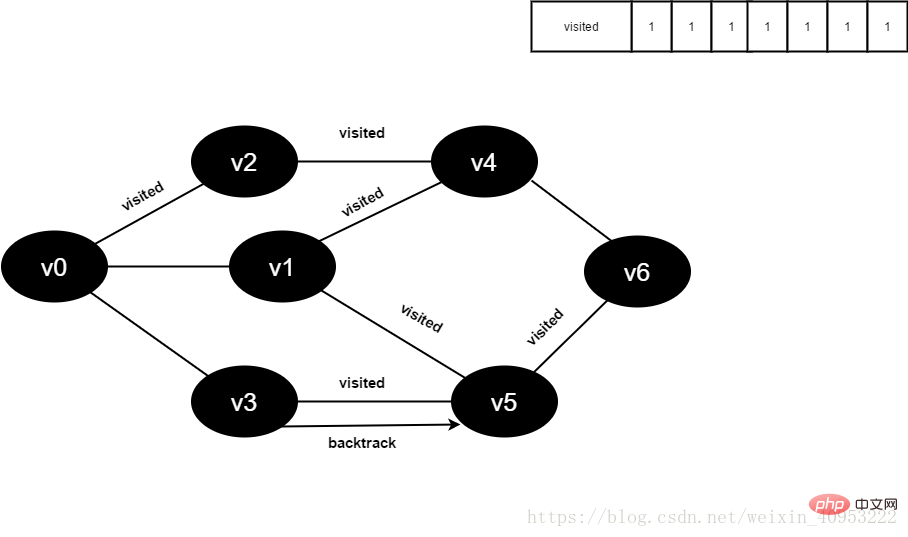
图4-2-15
16.访问v6的邻接点v4,判断visited[4],其值为1,不访问。
访问v6的邻接点v5,判断visited[5],其值为1,不访问。
v6所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5剩余邻接点。
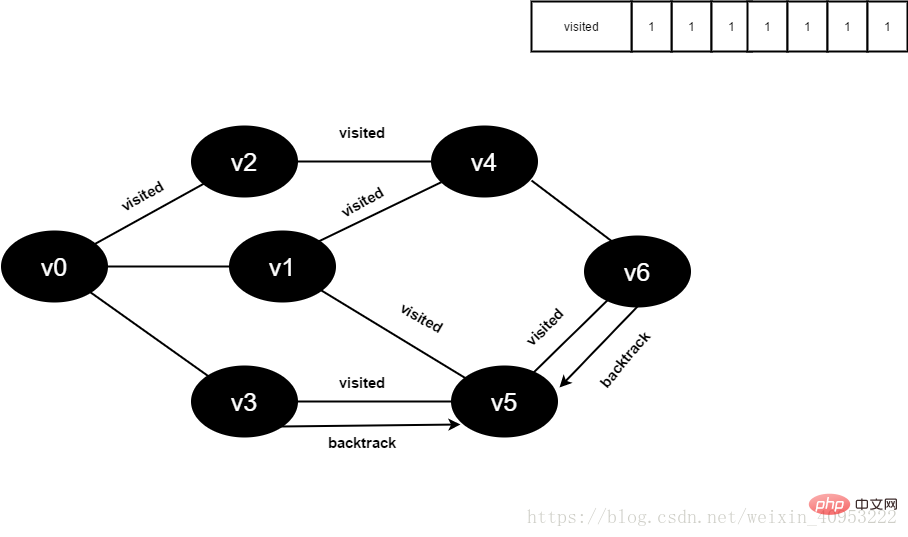
图4-2-16
17.v5所有邻接点均已被访问,回溯到其上一个顶点v1。
v1所有邻接点均已被访问,回溯到其上一个顶点v4,遍历v4剩余邻接点v6。
v4所有邻接点均已被访问,回溯到其上一个顶点v2。
v2所有邻接点均已被访问,回溯到其上一个顶点v1,遍历v1剩余邻接点v3。
v1所有邻接点均已被访问,搜索结束。
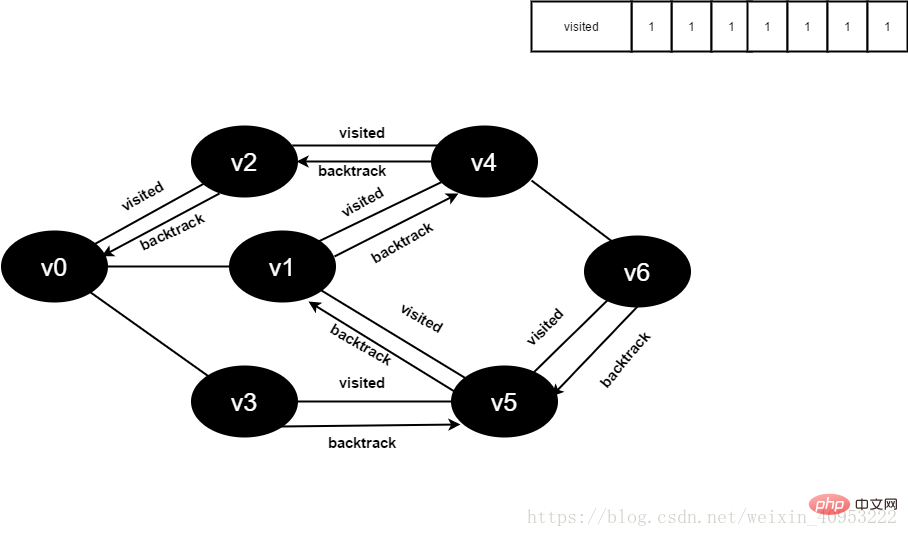
图4-2-17
4.3具体代码实现
4.3.1用邻接矩阵表示图的深度优先搜索
邻接矩阵的创建在上述已描述过,这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}4.3.2用邻接表表示图的深度优先搜素
邻接表的创建在上述已描述过,这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}
更多相关知识,请访问:PHP中文网!
以上是图的广度优先遍历类似于二叉树的什么?的详细内容。更多信息请关注PHP中文网其他相关文章!