某二叉树有5个度为2的结点，则该二叉树叶子结点数是多少？

在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

一棵深度为k，且有2^k-1个结点的二叉树，称为满二叉树。这种树的特点是每一层上的结点数都是最大结点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且或者最后一层是满的，或者是在右边缺少连续若干结点，则此二叉树为完全二叉树。具有n个结点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至少有2k-1个叶子结点，至多有2k-1个结点。

某二叉树有5个度为2的结点，则该二叉树叶子结点数是？

二叉树中的叶子结点数与度为2的结点数的关系是：度为2的结点数=叶子结点数-1；

所以，叶子结点数=度为2的结点数+1=6。

拓展：

二叉树是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：

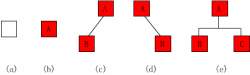
1. 空二叉树——如图(a)；

2. 只有一个根结点的二叉树——如图(b)；

3. 只有左子树——如图(c)；

4. 只有右子树——如图(d)；

5. 完全二叉树——如图(e)。

注意：尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。

类型

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

更多相关知识，请关注 PHP中文网！！

以上是某二叉树有5个度为2的结点，则该二叉树叶子结点数是多少？的详细内容。更多信息请关注PHP中文网其他相关文章！