c语言最小生成树的实现

1.最小生成树介绍

什么是最小生成树？

最小生成树（Minimum spanning tree，MST）是在一个给定的无向图G(V,E)中求一棵树T，使得这棵树拥有图G中的所有顶点，且所有边都是来自图G中的边，并且满足整棵树的边权值和最小。

2.prim算法

和Dijkstra算法很像！！请看如下Gif图，prim算法的核心思想是对图G(V,E)设置集合S，存放已被访问的顶点，然后每次从集合V-S中选择与集合S的最短距离最小的一个顶点（记为u），访问并加入集合S。之后，令顶点u为中间点，优化所有从u能到达的顶点v与集合s之间的最短距离。这样的操作执行n次，直到集合s中包含所有顶点。

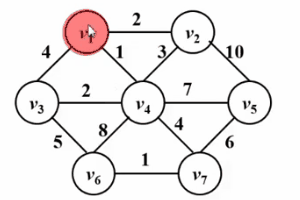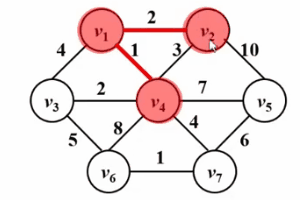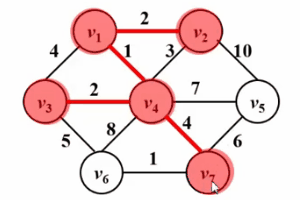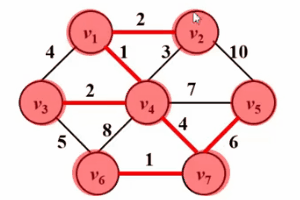
不同的是，Dijkstra算法中的dist是从源点s到顶点w的最短路径；而prim算法中的dist是从集合S到顶点w的最短路径，以下是他们的伪码描述对比，关于Dijkstra算法的详细描述请参考文章

算法实现：

#include<iostream>
#include<vector>
#define INF 100000
#define MaxVertex 105
typedef int Vertex; 
int G[MaxVertex][MaxVertex];
int parent[MaxVertex];   // 并查集 
int dist[MaxVertex]; // 距离 
int Nv;    // 结点 
int Ne;    // 边 
int sum;  // 权重和 
using namespace std; 
vector<Vertex> MST;  // 最小生成树 
// 初始化图信息 
void build(){
    Vertex v1,v2;
    int w;
    cin>>Nv>>Ne;
    for(int i=1;i<=Nv;i++){
        for(int j=1;j<=Nv;j++)
            G[i][j] = 0;  // 初始化图 
        dist[i] = INF;   // 初始化距离
        parent[i] = -1;  // 初始化并查集 
    }
    // 初始化点
    for(int i=0;i<Ne;i++){
        cin>>v1>>v2>>w;
        G[v1][v2] = w;
        G[v2][v1] = w;
    }
}
// Prim算法前的初始化 
void IniPrim(Vertex s){
    dist[s] = 0;
    MST.push_back(s);
    for(Vertex i =1;i<=Nv;i++)
        if(G[s][i]){
            dist[i] = G[s][i];
            parent[i] = s;
        } 
}
// 查找未收录中dist最小的点 
Vertex FindMin(){
    int min = INF;
    Vertex xb = -1;
    for(Vertex i=1;i<=Nv;i++)
        if(dist[i] && dist[i] < min){ 
            min = dist[i];
            xb = i;
        }
    return xb;
}
void output(){
    cout<<"被收录顺序："<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<MST[i]<<" ";
    cout<<"权重和为："<<sum<<endl; 
    cout<<"该生成树为："<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<parent[i]<<" ";
}
void Prim(Vertex s){
    IniPrim(s);
    while(1){
        Vertex v = FindMin();
        if(v == -1)
            break;
        sum += dist[v];
        dist[v] = 0;
        MST.push_back(v);
        for(Vertex w=1;w<=Nv;w++)
            if(G[v][w] && dist[w])
                if(G[v][w] < dist[w]){
                    dist[w] = G[v][w];
                    parent[w] = v;
                }
    }
}
int main(){
    build();
    Prim(1);
    output();
    return 0;
}

关于prim算法的更加详细讲解请参考视频 https://www.bilibili.com/video/av55114968?p=99

3.kruskal算法

Kruskal算法也可以用来解决最小生成树的问题，其算法思想很容易理解，典型的边贪心，其算法思想为：

● 在初始状态时隐去图中所有的边，这样图中每个顶点都是一个单独的连通块，一共有n个连通块

● 对所有边按边权从小到大进行排序

● 按边权从小到大测试所有边，如果当前测试边所连接的两个顶点不在同一个连通块中，则把这条测试边加入当前最小生成树中，否则，将边舍弃。

● 重复执行上一步骤，直到最小生成树中的边数等于总顶点数减一 或者测试完所有边时结束；如果结束时，最小生成树的边数小于总顶点数减一，说明该图不连通。

请看下面的Gif图！

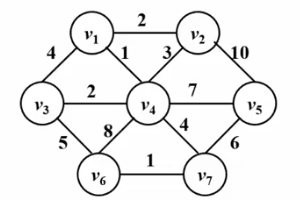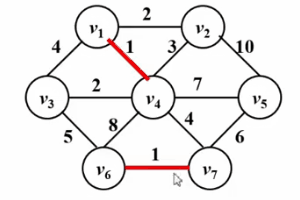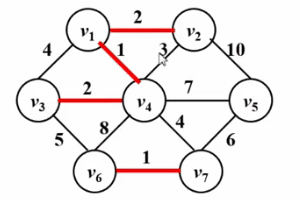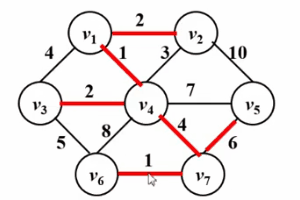
算法实现：

#include<iostream>
#include<string>
#include<vector>
#include<queue>
#define INF 100000
#define MaxVertex 105
typedef int Vertex; 
int G[MaxVertex][MaxVertex];
int parent[MaxVertex];   // 并查集最小生成树 
int Nv;    // 结点 
int Ne;    // 边 
int sum;  // 权重和 
using namespace std; 
struct Node{
    Vertex v1;
    Vertex v2;
    int weight; // 权重 
    // 重载运算符成最大堆 
    bool operator < (const Node &a) const
    {
        return weight>a.weight;
    }
};
vector<Node> MST;  // 最小生成树 
priority_queue<Node> q;   // 最小堆 
// 初始化图信息 
void build(){
    Vertex v1,v2;
    int w;
    cin>>Nv>>Ne;
    for(int i=1;i<=Nv;i++){
        for(int j=1;j<=Nv;j++)
            G[i][j] = 0;  // 初始化图
        parent[i] = -1;
    }
    // 初始化点
    for(int i=0;i<Ne;i++){
        cin>>v1>>v2>>w;
        struct Node tmpE;
        tmpE.v1 = v1;
        tmpE.v2 = v2;
        tmpE.weight = w;
        q.push(tmpE); 
    }
}
//  路径压缩查找 
int Find(int x){
    if(parent[x] < 0)
        return x;
    else
        return parent[x] = Find(parent[x]);
} 
//  按秩归并 
void Union(int x1,int x2){
    if(parent[x1] < parent[x2]){
        parent[x1] += parent[x2];
        parent[x2] = x1;
    }else{
        parent[x2] += parent[x1];
        parent[x1] = x2;
    }
} 
void Kruskal(){
    // 最小生成树的边不到 Nv-1 条且还有边 
    while(MST.size()!= Nv-1 && !q.empty()){
        Node E = q.top();  // 从最小堆取出一条权重最小的边
        q.pop(); // 出队这条边 
        if(Find(E.v1) != Find(E.v2)){  // 检测两条边是否在同一集合 
            sum += E.weight; 
            Union(E.v1,E.v2);     // 并起来 
            MST.push_back(E);
        }
    }
    
} 
void output(){
    cout<<"被收录顺序："<<endl; 
    for(Vertex i=0;i<Nv;i++)
        cout<<MST[i].weight<<" ";
    cout<<"权重和为："<<sum<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<parent[i]<<" ";
    cout<<endl;
}
int main(){
    build();
    Kruskal();
    output();
    return 0;
}

关于kruskal算法更详细的讲解请参考视频 https://www.bilibili.com/video/av55114968?p=100

推荐课程：C语言教程  

以上是c语言最小生成树的实现的详细内容。更多信息请关注PHP中文网其他相关文章！