数据结构时间复杂度
- 王林原创
- 2019-10-30 16:07:388850浏览

什么是时间复杂度?
算法中某个函数有n次基本操作重复执行,用T(n)表示,现在有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数,记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
通俗一点讲,其实所谓的时间复杂度,就是找了一个同样曲线类型的函数f(n)来表示这个算法的在n不断变大时的趋势 。当输入量n逐渐加大时,时间复杂性的极限情形称为算法的“渐近时间复杂性”。
计算时间复杂度的方法:
1、用常数1代替运行时间中的所有加法常数
2、修改后的运行次数函数中,只保留最高阶项
3、去除最高阶项的系数
按数量级递增排列,常见的时间复杂度有:
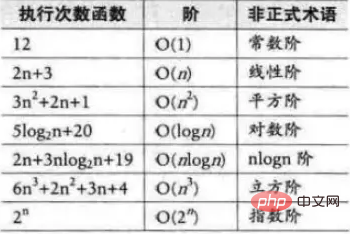
以上是数据结构时间复杂度的详细内容。更多信息请关注PHP中文网其他相关文章!
声明:
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系admin@php.cn
上一篇:电脑无法打印图片,什么原因下一篇:数据结构研究的内容涉及

