本篇文章给大家带来的内容是关于python中K-近邻算法的原理与实现(附源码),有一定的参考价值,有需要的朋友可以参考一下,希望对你有所帮助。
k-近邻算法通过测量不同特征值之间的距离方法进行分类。
k-近邻算法原理
对于一个存在标签的训练样本集,输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,根据算法选择样本数据集中前k个最相似的数据,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
k-近邻算法实现
这里只是对单个新数据的预测,对同时多个新数据的预测放在后文中。
假定存在训练样本集 X_train(X_train.shape=(10, 2)),对应的标记 y_train(y_train.shape=(10,),包含0、1),使用 matplotlib.pyplot 作图表示如下(绿色的点表示标记0,红色的点表示标记1):
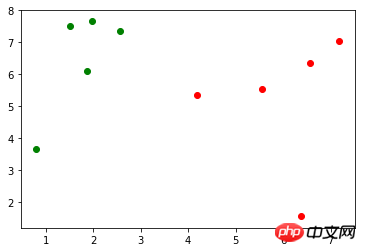
现有一个新的数据:x(x = np.array([3.18557125, 6.03119673])),作图表示如下(蓝色的点):
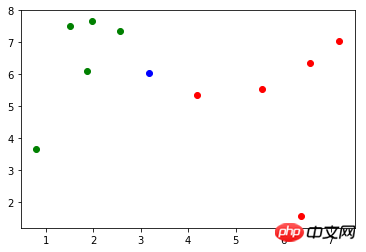
首先,使用欧拉距离公式计算 x 到 X_train 中每个样本的距离:
import math distances = [math.sqrt(np.sum((x_train - x) ** 2)) for x_train in X_train]
第二,对 distances 进行升序操作,使用 np.argsort() 方法返回排序后的索引,而不会对原数据的顺序有任何影响:
import numpy as np nearest = np.argsort(distances)
第三,取 k 个距离最近的样本对应的标记:
topK_y = [y_train[i] for i in nearest[:k]]
最后,对这 k 个距离最近的样本对应的标记进行统计,找出占比最多标记即为 x 的预测分类,此例的预测分类为0:
from collections import Counter votes = Counter(topK_y) votes.most_common(1)[0][0]
将上面的代码封装到一个方法中:
import numpy as np import math from collections import Counter def kNN(k, X_train, y_train, x): distances = [math.sqrt(np.sum((x_train - x) ** 2)) for x_train in X_train] nearest = np.argsort(distances) topK_y = [y_train[i] for i in nearest[:k]] votes = Counter(topK_y) return votes.most_common(1)[0][0]
Scikit Learn 中的 k-近邻算法
一个典型的机器学习算法流程是将训练数据集通过机器学习算法训练(fit)出模型,通过这个模型来预测输入样例的结果。
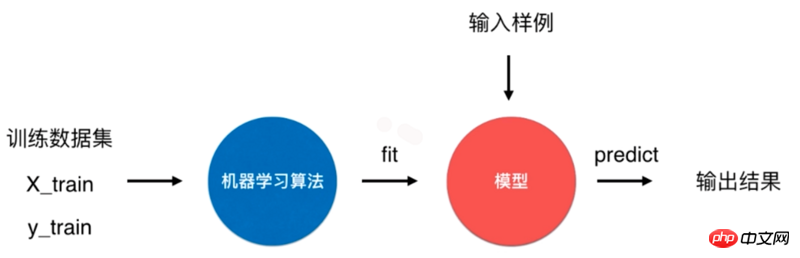
对于 k-近邻算法来说,它是一个特殊的没有模型的算法,但是我们将其训练数据集看作是模型。Scikit Learn 中就是怎么处理的。
Scikit Learn 中 k-近邻算法使用
Scikit Learn 中 k-邻近算法在 neighbors 模块中,初始化时传入参数 n_neighbors 为 6,即为上面的 k:
from sklearn.neighbors import KNeighborsClassifier kNN_classifier = KNeighborsClassifier(n_neighbors=6)
fit() 方法根据训练数据集“训练”分类器,该方法会返回分类器本身:
kNN_classifier.fit(X_train, y_train)
predict() 方法预测输入的结果,该方法要求传入的参数类型为矩阵。因此,这里先对 x 进行 reshape 操作:
X_predict = x.reshape(1, -1) y_predict = kNN_classifier.predict(X_predict)
y_predict 值为0,与前面实现的 kNN 方法结果一致。
实现 Scikit Learn 中的 KNeighborsClassifier 分类器
定义一个 KNNClassifier 类,其构造器方法传入参数 k,表示预测时选取的最相似数据的个数:
class KNNClassifier: def __init__(self, k): self.k = k self._X_train = None self._y_train = None
fit() 方法训练分类器,并且返回分类器本身:
def fit(self, X_train, y_train): self._X_train = X_train self._y_train = y_train return self
predict() 方法对待测数据集进行预测,参数 X_predict 类型为矩阵。该方法使用列表解析式对 X_predict 进行了遍历,对每个待测数据调用了一次 _predict() 方法。
def predict(self, X_predict): y_predict = [self._predict(x) for x in X_predict] return np.array(y_predict) def _predict(self, x): distances = [math.sqrt(np.sum((x_train - x) ** 2)) for x_train in self._X_train] nearest = np.argsort(distances) topK_y = [self._y_train[i] for i in nearest[:self.k]] votes = Counter(topK_y) return votes.most_common(1)[0][0]
算法准确性
模型存在的问题
上面通过训练样本集训练出了模型,但是并不知道这个模型的好坏,还存在两个问题。
如果模型很坏,预测的结果就不是我们想要的。同时实际情况中,很难拿到真实的标记(label),无法对模型进行检验。
训练模型时训练样本没有包含所有的标记。
对于第一个问题,通常将样本集中一定比例(如20%)的数据作为测试数据,其余数据作为训练数据。
以 Scikit Learn 中提供的鸢尾花数据为例,其包含了150个样本。
import numpy as np from sklearn import datasets iris = datasets.load_iris() X = iris.data y = iris.target
现在将样本分为20%示例测试数据和80%比例训练数据:
test_ratio = 0.2 test_size = int(len(X) * test_ratio) X_train = X[test_size:] y_train = y[test_size:] X_test = X[:test_size] y_test = y[:test_size]
将 X_train 和 y_train 作为训练数据用于训练模型,X_test 和 y_test 作为测试数据验证模型准确性。
对于第二个问题,还是以 Scikit Learn 中提供的鸢尾花数据为例,其标记 y 的内容为:
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
发现0、1、2是以顺序存储的,在将样本划分为训练数据和测试数据过程中,如果训练数据中才对标记只包含0、1,这样的训练数据对于模型的训练将是致命的。以此,应将样本数据先进行随机处理。
np.random.permutation() 方法传入一个整数 n,会返回一个区间在 [0, n) 且随机排序的一维数组。将 X 的长度作为参数传入,返回 X 索引的随机数组:
shuffle_indexes = np.random.permutation(len(X))
将随机化的索引数组分为训练数据的索引与测试数据的索引两部分:
test_ratio = 0.2 test_size = int(len(X) * test_ratio) test_indexes = shuffle_indexes[:test_size] train_indexes = shuffle_indexes[test_size:]
再通过两部分的索引将样本数据分为训练数据和测试数据:
X_train = X[train_indexes] y_train = y[train_indexes] X_test = X[test_indexes] y_test = y[test_indexes]
可以将两个问题的解决方案封装到一个方法中,seed 表示随机数种子,作用在 np.random 中:
import numpy as np def train_test_split(X, y, test_ratio=0.2, seed=None): if seed: np.random.seed(seed) shuffle_indexes = np.random.permutation(len(X)) test_size = int(len(X) * test_ratio) test_indexes = shuffle_indexes[:test_size] train_indexes = shuffle_indexes[test_size:] X_train = X[train_indexes] y_train = y[train_indexes] X_test = X[test_indexes] y_test = y[test_indexes] return X_train, X_test, y_train, y_test
Scikit Learn 中封装了 train_test_split() 方法,放在了 model_selection 模块中:
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
算法正确率
通过 train_test_split() 方法对样本数据进行了预处理后,开始训练模型,并且对测试数据进行验证:
from sklearn.neighbors import KNeighborsClassifier kNN_classifier = KNeighborsClassifier(n_neighbors=6) kNN_classifier.fit(X_train, y_train) y_predict = kNN_classifier.predict(X_test)
y_predict 是对测试数据 X_test 的预测结果,其中与 y_test 相等的个数除以 y_test 的个数就是该模型的正确率,将其和 y_test 进行比较可以算出模型的正确率:
def accuracy_score(y_true, y_predict): return sum(y_predict == y_true) / len(y_true)
调用该方法,返回一个小于等于1的浮点数:
accuracy_score(y_test, y_predict)
同样在 Scikit Learn 的 metrics 模块中封装了 accuracy_score() 方法:
from sklearn.metrics import accuracy_score accuracy_score(y_test, y_predict)
Scikit Learn 中的 KNeighborsClassifier 类的父类 ClassifierMixin 中有一个 score() 方法,里面就调用了 accuracy_score() 方法,将测试数据 X_test 和 y_test 作为参数传入该方法中,可以直接计算出算法正确率。
class ClassifierMixin(object): def score(self, X, y, sample_weight=None): from .metrics import accuracy_score return accuracy_score(y, self.predict(X), sample_weight=sample_weight)
超参数
前文中提到的 k 是一种超参数,超参数是在算法运行前需要决定的参数。 Scikit Learn 中 k-近邻算法包含了许多超参数,在初始化构造函数中都有指定:
def __init__(self, n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None, **kwargs): # code here
这些超参数的含义在源代码和官方文档[scikit-learn.org]中都有说明。
算法优缺点
k-近邻算法是一个比较简单的算法,有其优点但也有缺点。
优点是思想简单,但效果强大, 天然的适合多分类问题。
缺点是效率低下,比如一个训练集有 m 个样本,n 个特征,则预测一个新的数据的算法复杂度为 O(m*n);同时该算法可能产生维数灾难,当维数很大时,两个点之间的距离可能也很大,如 (0,0,0,...,0) 和 (1,1,1,...,1)(10000维)之间的距离为100。
源码地址
以上是python中K-近邻算法的原理与实现(附源码)的详细内容。更多信息请关注PHP中文网其他相关文章!
 特斯拉自动驾驶算法和模型解读Apr 11, 2023 pm 12:04 PM
特斯拉自动驾驶算法和模型解读Apr 11, 2023 pm 12:04 PM特斯拉是一个典型的AI公司,过去一年训练了75000个神经网络,意味着每8分钟就要出一个新的模型,共有281个模型用到了特斯拉的车上。接下来我们分几个方面来解读特斯拉FSD的算法和模型进展。01 感知 Occupancy Network特斯拉今年在感知方面的一个重点技术是Occupancy Network (占据网络)。研究机器人技术的同学肯定对occupancy grid不会陌生,occupancy表示空间中每个3D体素(voxel)是否被占据,可以是0/1二元表示,也可以是[0, 1]之间的
 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
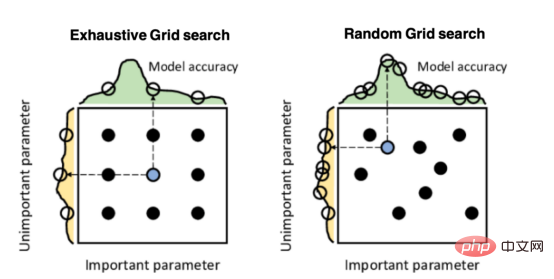 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
 因果推断主要技术思想与方法总结Apr 12, 2023 am 08:10 AM
因果推断主要技术思想与方法总结Apr 12, 2023 am 08:10 AM导读:因果推断是数据科学的一个重要分支,在互联网和工业界的产品迭代、算法和激励策略的评估中都扮演者重要的角色,结合数据、实验或者统计计量模型来计算新的改变带来的收益,是决策制定的基础。然而,因果推断并不是一件简单的事情。首先,在日常生活中,人们常常把相关和因果混为一谈。相关往往代表着两个变量具有同时增长或者降低的趋势,但是因果意味着我们想要知道对一个变量施加改变的时候会发生什么样的结果,或者说我们期望得到反事实的结果,如果过去做了不一样的动作,未来是否会发生改变?然而难点在于,反事实的数据往往是
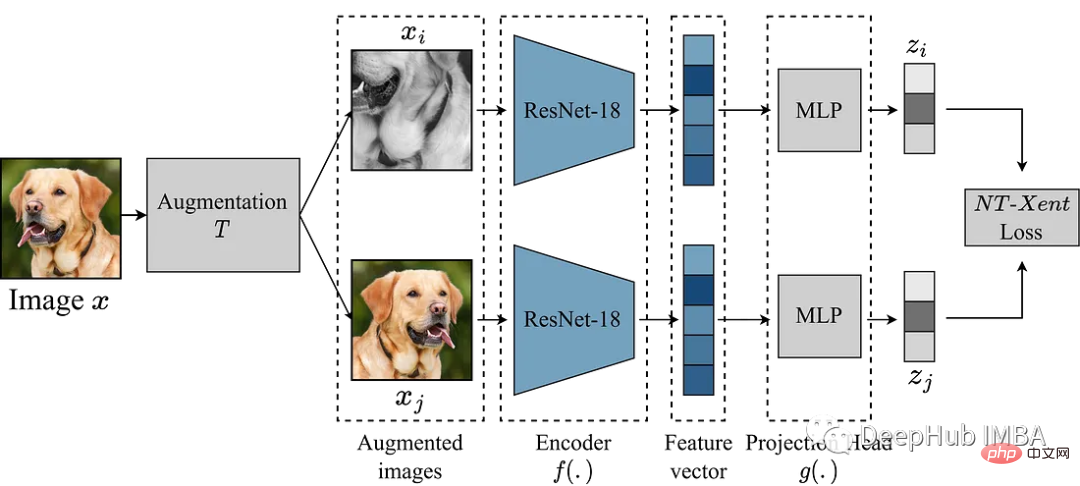 使用Pytorch实现对比学习SimCLR 进行自监督预训练Apr 10, 2023 pm 02:11 PM
使用Pytorch实现对比学习SimCLR 进行自监督预训练Apr 10, 2023 pm 02:11 PMSimCLR(Simple Framework for Contrastive Learning of Representations)是一种学习图像表示的自监督技术。 与传统的监督学习方法不同,SimCLR 不依赖标记数据来学习有用的表示。 它利用对比学习框架来学习一组有用的特征,这些特征可以从未标记的图像中捕获高级语义信息。SimCLR 已被证明在各种图像分类基准上优于最先进的无监督学习方法。 并且它学习到的表示可以很容易地转移到下游任务,例如对象检测、语义分割和小样本学习,只需在较小的标记
 盒马供应链算法实战Apr 10, 2023 pm 09:11 PM
盒马供应链算法实战Apr 10, 2023 pm 09:11 PM一、盒马供应链介绍1、盒马商业模式盒马是一个技术创新的公司,更是一个消费驱动的公司,回归消费者价值:买的到、买的好、买的方便、买的放心、买的开心。盒马包含盒马鲜生、X 会员店、盒马超云、盒马邻里等多种业务模式,其中最核心的商业模式是线上线下一体化,最快 30 分钟到家的 O2O(即盒马鲜生)模式。2、盒马经营品类介绍盒马精选全球品质商品,追求极致新鲜;结合品类特点和消费者购物体验预期,为不同品类选择最为高效的经营模式。盒马生鲜的销售占比达 60%~70%,是最核心的品类,该品类的特点是用户预期时
 研究表明强化学习模型容易受到成员推理攻击Apr 09, 2023 pm 08:01 PM
研究表明强化学习模型容易受到成员推理攻击Apr 09, 2023 pm 08:01 PM译者 | 李睿 审校 | 孙淑娟随着机器学习成为人们每天都在使用的很多应用程序的一部分,人们越来越关注如何识别和解决机器学习模型的安全和隐私方面的威胁。 然而,不同机器学习范式面临的安全威胁各不相同,机器学习安全的某些领域仍未得到充分研究。尤其是强化学习算法的安全性近年来并未受到太多关注。 加拿大的麦吉尔大学、机器学习实验室(MILA)和滑铁卢大学的研究人员开展了一项新研究,主要侧重于深度强化学习算法的隐私威胁。研究人员提出了一个框架,用于测试强化学习模型对成员推理攻击的脆弱性。 研究
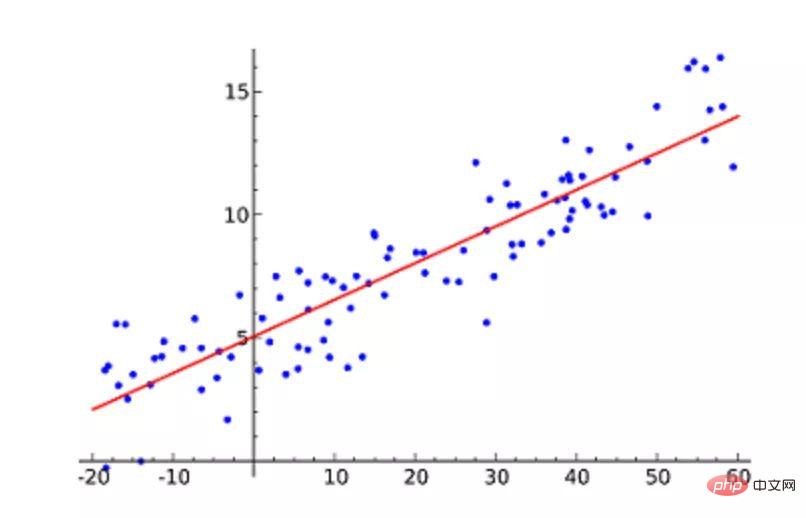 机器学习必知必会十大算法!Apr 12, 2023 am 09:34 AM
机器学习必知必会十大算法!Apr 12, 2023 am 09:34 AM1.线性回归线性回归(Linear Regression)可能是最流行的机器学习算法。线性回归就是要找一条直线,并且让这条直线尽可能地拟合散点图中的数据点。它试图通过将直线方程与该数据拟合来表示自变量(x 值)和数值结果(y 值)。然后就可以用这条线来预测未来的值!这种算法最常用的技术是最小二乘法(Least of squares)。这个方法计算出最佳拟合线,以使得与直线上每个数据点的垂直距离最小。总距离是所有数据点的垂直距离(绿线)的平方和。其思想是通过最小化这个平方误差或距离来拟合模型。例如


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

SublimeText3 英文版
推荐:为Win版本,支持代码提示!

SublimeText3汉化版
中文版,非常好用

WebStorm Mac版
好用的JavaScript开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

SublimeText3 Linux新版
SublimeText3 Linux最新版





