js教程

前端中排序算法实例详解

php中世界最好的语言

May 24, 2018 pm 01:42 PM

实例算法详解

这次给大家带来前端中排序算法实例详解，前端中排序算法使用的注意事项有哪些，下面就是实战案例，一起来看一下。

前言

前天看到知乎上有一篇文章在吐槽阮一峰老师的快速排序算法,这里插一句题外话,我觉得人非圣贤孰能无过,尽信书不如无书,学习的过程也就是不断发现错误改正错误的过程,有人帮我们纠正了这个错误我们应该开心,但是我觉得不应该批判阮一峰老师,他也在不断地学习,不断地纠错成长,所以大家都一样,无所谓误导,如果出错的不是他,是更厉害的牛人呢?JavaScript的作者呢?所以大家都会出错,我们也应该多思考,抱着怀疑的态度接纳,时刻思考这是不是最优的解法,还有没有更好的呢,我想这才是我们应该做的.
而我,作为一个计算机专业的前端,却不能很好地实现各种思想的排序算法,我觉得很惭愧,所以我就抽时间仔细查看了<<数据结构与算法分析：C语言描述+中文版.pdf>>这本书,下面我就对我理解的各种思想的排序算法做一下总结,希望可以给大家一些参考和收获,如有不妥之处,烦请指出,也可以分享你们觉得更好地想法,我觉得大家一起学习一起进步是最快乐的事~

1. 应当熟悉的相关概念

1.1 时间复杂度

(1) 时间复杂度的概念
算法的时间复杂度是一个函数,他定性地描述了某个算法的运行时间,常用大O符号,不包括这个函数的低阶项和高阶项系数.
(2) 计算方法

一般情况下,算法中基本操作的执行次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不为零的常数,则f(n)是T(n)的同数量级函数,记作T(n) = O(f(n)),称O(f(n))为算法的渐进时间复杂度,简称为时间复杂度.
分析: 随时模块n的增大,算法的执行时间的增长率和f(n)的增长率成正比,所以f(n)越小,算法的时间复杂度越低,算法的效率越高.
在计算时间复杂度的时候,先找出算法的基本操作,然后计算出基本操作的执行次数,找出T(n)的同数量级f(n)(它的同数量级一般有以下: 1, log₂n,n,nlog₂n,n的平方,n的三次方),若T(n) / f(n)求极限得到一常数c,则时间复杂度T(n) = O(f(n)):

举例如下:

for(i = 1; i<= n; i++) {
    for(j = 1; j <= n; j++) {
        c[i][j] = 0;   // 该步骤属于基本操作的执行次数: n的平方
        for( k= 1;k <= n; k++) {
            c[i][j] += a[i][k] * b[k][j];   // 该步骤属于基本操作的执行次数: n的三次方
        }
    }
}

我们可以得到T(n) = n^3 + n^2,我们可以确定n^3为T(n)的同数量级,f(n)=n^3;然后T(n) / f(n) = 1 + 1/n 求极限为常数1,所以该算法的时间复杂度为:
T(n) = O(n^3);

说明: 为了方便我接下来都是使用N来代指数组元素个数的.

2. 排序算法

2.1 冒泡排序

2.1.1 主要思想:

冒泡排序的主要思想就是对一个长度为n的数组进行遍历, i从n-1到1的,数组的前i个元素的最大值放在i位置上,假想冒泡排序是一个竖着的水柱,遍历的过程就是,大的值(重的)不断沉下来,小的值(轻的)不断浮上去,这样遍历结束后,每个位置上的值都比他前面的值大,排序结束.

2.1.2 时间复杂度

最坏情况下的时间复杂度: o(n^2);
最好情况下的时间复杂度: o(n^2);

2.1.3 排序过程图解:

图解中的出循环是退出内层循环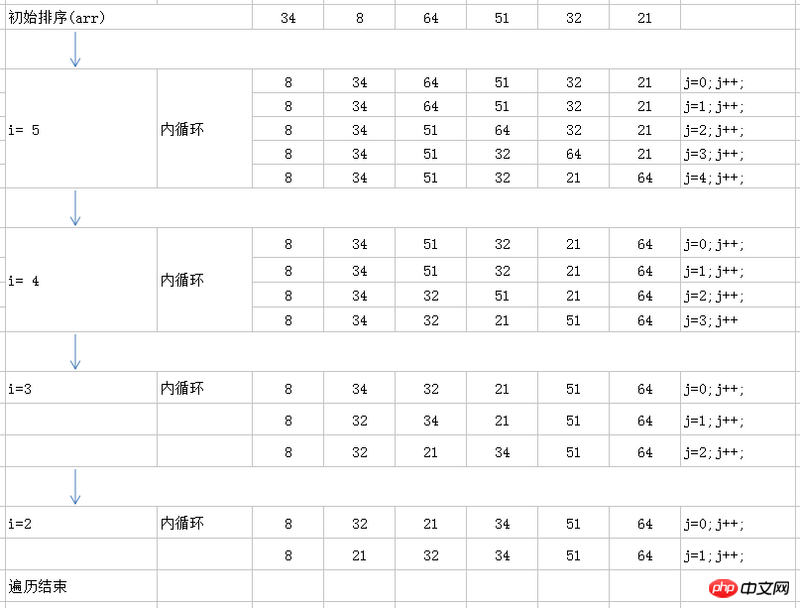
冒泡排序图解

2.1.4 代码实现:

冒泡排序-非递归实现

function bubbleSort(arr) {
    for(var i = arr.length - 1; i > 1; i--) {
        for(var j=0; j < i; j++) {
            if(arr[j] > arr[j+1]) {
                var temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
    return arr;
}
var arr =  [34,8,64,51,32,21];
bubbleSort(arr);  // [8, 21, 32, 34, 51, 64]

冒泡排序-递归实现

function bubbleSort(arr, n) {
    if(n <= 1) {
        return arr;
    } else {
        for(var j=0; j < n - 1; j++) {
            if(arr[j] > arr[j+1]) {
                var temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
        return bubbleSort(arr, --n);
    }
}
var arr =  [34,8,64,51,32,21];
bubbleSort(arr, arr.length);  // [8, 21, 32, 34, 51, 64]

2.2 插入排序

2.2.1 主要思想:

插入排序有 n-1 趟排序组成,对于 i=1 到 i=n-1 趟,内层循环j从 i 到 1, 如果这其中有 j-1 位置上的元素大于 i 位置上的元素,就将该元素后移,知道条件不成立退出循环,这个时候大的值都被移动到后面了,j这个位置就是i位置上的元素应该在的位置.这样保证了每次循环i位置前的所有元素都是排好序的,新的循环就只需要将 i 位置上的元素和 j-1(也就是初始的 i-1) 位置上的元素作比较,如果大于则无需再往前比较,如果小于则继续往前比较后移.

2.2.2 时间复杂度

最坏情况下的时间复杂度: o(n^2);
最好情况下的时间复杂度: o(n);

2.2.3 排序过程图解:

图解中的出循环是退出内层循环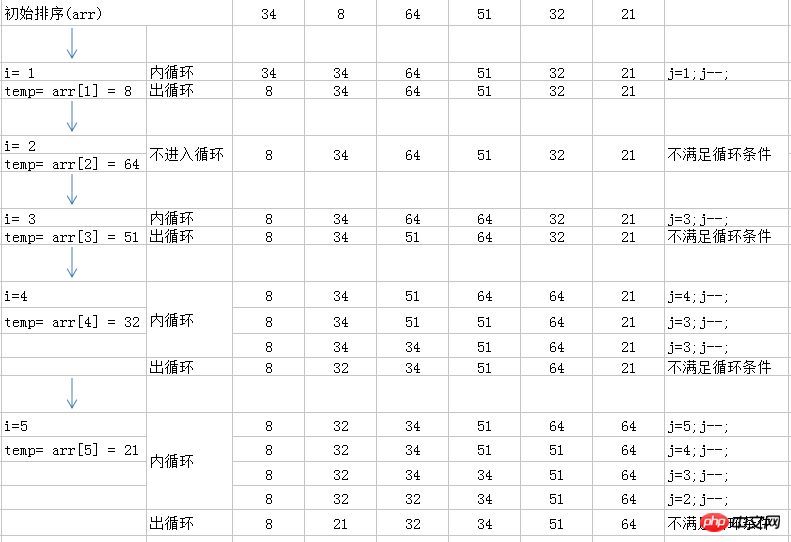
插入排序过程图解

2.2.4 代码实现

插入排序-非递归实现

function insertSort(arr) {
    var n = arr.length,temp = 0;
    for(var i = 1; i < n; i++) {
        temp = arr[i];
        for(j = i; j > 0 && arr[j-1] > temp; j--) {
            arr[j] = arr[j - 1];
        }
        arr[j] = temp;
    }
    return arr;
}
var arr =  [34,8,64,51,32,21];
insertSort(arr);  // [8, 21, 32, 34, 51, 64]

插入排序-递归实现

function insertSort(arr, n) {
    if(n > 0 && n < arr.length){
        var i = j = n, temp = arr[n];
        while(j > 0 && arr[j - 1] > temp) {
            arr[j] = arr[j - 1];
            j--;
        }
        arr[j] = temp;
        i++;
        return insertSort(arr, i);
    }
    return arr;
}
var arr =  [34,8,64,51,32,21];
insertSort(arr, 1); // [8, 21, 32, 34, 51, 64]; // 这个函数的调用限定了第一次调用n的值只能传1

2.3 快速排序

顾名思义,快速排序是在实践中最快的已知排序算法,它的平均运行时间是O(Nlog₂N).快速排序的关键在于枢纽元的选取,有一种比较推荐的选取方法就是选取左端的值,右端的值,中间位置的值(L(left + right) / 2)这三个数的中位数.举例: 输入为8,1,4,9,6,3,5,2,7,0, 左边元素8, 右边元素0,中间位置上的元素L(0+9)/2是4位置上的元素是6,L在表示向下取整.
8,0,6的中位数,先排序0,6,8, 这三个数的中位数是6.

2.3.1 基本思想

通过一趟排序将要排序的部分分割成独立的两部分,其中一部分数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据进行快速排序,整个排序过程可以递归进行,依次达到整个数据变成有序序列.

2.3.2 实现步骤

第一步: 设置两个变量i,j,排序开始的时候: i=left,j=right-1,left和right分别表示要进行快速排序序列的起始索引和结束索引;
第二步: 从数组中随机选取一个元素,将其与arr[left]进行交换,即privot = arr[left],保证每一次的基准值都在序列的最左边;
第三步: 由j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于privot 的值arr[j],将arr[i]与arr[j]互换;
第四步: 从i开始向后搜索,即由前开始向后搜索(i++),找到一个大于privot 的arr[i],将arr[i]与arr[j]互换;
第五步: 重复第三步和第四步,直到不满足i第六步: 重复第二步到第四步,依次对i位置左右两边的元素进行快速排序,直到left大于等于right为止.

2.3.3 时间复杂度:

平均情况下的时间复杂度: o(nlog₂n);
最好情况下的时间复杂度: o(n);

2.3.4 排序过程图解

快速排序过程图解

2.3.5 代码实现:

快速排序-递归实现

function quickSort(arr, left, right) {
    if(left >= right) return;
    var i = left;
    var j = right - 1;
    var privot = arr[left];
    //console.log(privot);
    while(i < j) {
        while(i<j  && arr[j] >= privot) j--;
        arr[i] = arr[j];
        while(i<j && arr[i] <= privot) i++;
        arr[j]=arr[i];
    }
    arr[i]=privot;
    quickSort(arr, left, i);
    quickSort(arr, i+1, right);
}
var arr = [49,38,65,97,76,13,27,49,55,04];
quickSort(arr, 0, arr.length);

快速排序-非递归实现

function mainProduce(arr, left, right) {
        var i = left, j = right - 1;
        var rendomIndex = Math.floor(Math.random() * (j - i)) + left;
        var temp = arr[left];arr[left] = arr[rendomIndex];arr[rendomIndex] = temp;
        var privot = arr[left];
        while(i < j) {
            while(i<j  && arr[j] >= privot) j--;
            var temp = arr[i];arr[i] = arr[j];arr[j] = temp;
            while(i<j && arr[i] <= privot) i++;
            var temp = arr[j];arr[j] = arr[i];arr[i] = temp;
        }
        arr[i]=privot;
        return i;
    }
    function quickSort(arr, left, right) {
        var s = [];
        if(left < right) {
            var mid = mainProduce(arr, left, right);
            if(mid > left + 1) {
                s.push(left);s.push(mid);
            }
            if(mid < right - 1) {
                s.push(mid + 1);s.push(right);
            }
            
            while(s.length !== 0) {
                console.log(s);
                right = s.pop();
                left = s.pop();
                mid = mainProduce(arr, left, right);
                if(mid > left + 1) {
                    s.push(left);s.push(mid);
                }
                if(mid < right - 1) {
                    s.push(mid + 1);s.push(right);
                }
            }
        }
        return arr;
    }
    var arr = [49,38,65,97,76,13,27,49,55,04];
    quickSort(arr, 0, arr.length);

2.4 希尔排序

2.4.1 主要思想

希尔排序是把记录按照下标的一定增量分组,对每组使用插入排序;随着增量逐渐减少,分割的数组越来越大,当增量减至1,整个数组排序完成,算法终止.

2.4.2主要步骤

第一步: 选取一个增量d,初始值是Math.floor(len/2);
第二步: 然后将数组中间隔为增量d的组成新的分组,然后对这个分组的元素排序,完成排序后,增量除以2得到新的增量;
第三步: 重复第二步,直到增量为1,间隔为1的元素组成的分组就是整个数组,然后再对整个数组进行插入排序,得到最后排序后数组.

希尔排序是不稳定的,它在不断地交换的过程中会改变原来相等的元素的顺序.

2.4.3 时间复杂度

平均情况下的时间复杂度: o(nlog₂n);
最好情况下的时间复杂度: o(n);

2.4.4 排序过程图解

排序过程图解

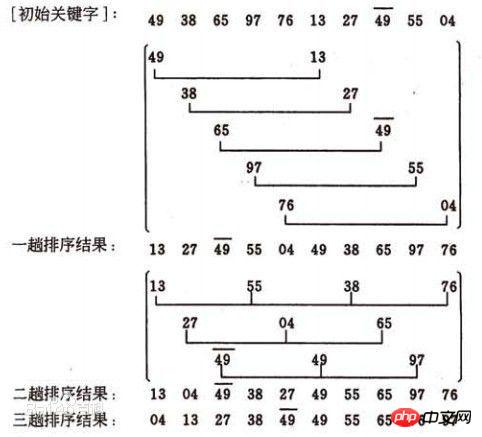
图片源于自百度百科: 图片来源

2.4.5 代码实现:

希尔排序-递归实现

function shellSort(arr, increment) {
    var len = arr.length;
    if(increment > 0) {
        for(var i = increment; i < len; i++) {
            for(var j = i - increment; j >= 0 && arr[j] > arr[j + increment]; j -= increment) {
                    var temp = arr[j];
                    arr[j] = arr[j + increment];
                    arr[j + increment] = temp;
            }
        }
        return shellSort(arr, Math.floor(increment/2));
    }
     return arr; 
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr, Math.floor(arr.length / 2));</p>
<h4 id="希尔排序-非递归实现">希尔排序-非递归实现</h4>
<pre class="brush:php;toolbar:false">function shellSort(arr) {
        var len = arr.length;
        for(var increment = Math.floor(len / 2); increment > 0; increment = Math.floor(increment / 2)) {
                for(var i = increment; i < len; i++) {
                        for(var j = i - increment; j >= 0 && arr[j] > arr[j + increment]; j -= increment) {
                                var temp = arr[j];
                                arr[j] = arr[j + increment];
                                arr[j + increment] = temp;
                        }
                }
        }
        return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr);

2.5 归并排序

2.5.1 主要思想

第一步: 将一个数组以中间值截取为为两个数组,分别将其排好序;
第二步: 申请一个空间,使其大小为两个已经排序的序列之和,该空间用来存放合并后的序列;
第三步: 设定两个指针,分别指向两个已排序序列的起始位置;
第四步: 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置.
重复第四步直到有一个某一指针超出序列尾;
将另一序列的所有元素复制到合并序列尾.
归并排序是稳定的,它在不会改变原来相等的元素的顺序.

2.5.2 时间复杂度

平均情况下的时间复杂度: O(nlog₂n);
最好情况下的时间复杂度: O(nlog₂n) ;

2.5.3 排序过程图解

归并排序过程图解

2.5.4 代码实现:

归并排序-递归实现

var result = [];
function mergeArray(left, right) {
    result = [];
    while(left.length > 0 && right.length > 0) {
        if(left[0] < right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
            }
    }
    return result.concat(left).concat(right);
}
function mergerSort(arr) {
    if(arr.length <= 1) {
        return arr;
    }
    var middle = Math.floor(arr.length / 2);
    var left = arr.slice(0, middle);
    var right = arr.slice(middle);
    return mergeArray(mergerSort(left), mergerSort(right));
}
var arr = [49,38,65,97,76,13,27,49,55,04];
mergerSort(arr, 0, arr.length);

相信看了本文案例你已经掌握了方法，更多精彩请关注php中文网其它相关文章！