这篇文章主要介绍了Python基于递归算法实现的汉诺塔与Fibonacci数列,结合实例形式分析了汉诺塔与Fibonacci数列的递归实现技巧,需要的朋友可以参考下
本文实例讲述了Python基于递归算法实现的汉诺塔与Fibonacci数列。分享给大家供大家参考,具体如下:
这里我们通过2个例子,学习python中递归的使用。
1. 找出Fibonacci数列中,下标为 n 的数(下标从0计数)
Fibonacci数列的形式是这样的:0,1,1,2,3,5,8,13……
① 使用while循环,python2代码如下:
def fib(n):
a,b=0,1
count=0
while count<n:
a,b=b,a+b
count=count+1
print a运行结果如下:
>>> fib(0)
0
>>> fib(1)
1
>>> fib(2)
1
>>> fib(3)
2
>>> fib(4)
3
>>> fib(5)
5
② 使用递归(递归必须要有边界条件),python2代码如下:
def fib(n):
if n==0 or n==1:#递归的边界条件
return n
else:
return fib(n-1)+fib(n-2)运行结果如下:
>>> fib(0)
0
>>> fib(1)
1
>>> fib(2)
1
>>> fib(3)
2
>>> fib(4)
3
>>> fib(5)
5
递归是最能表现计算思维的算法之一,我们以f(4)为例,看一下递归的执行过程:
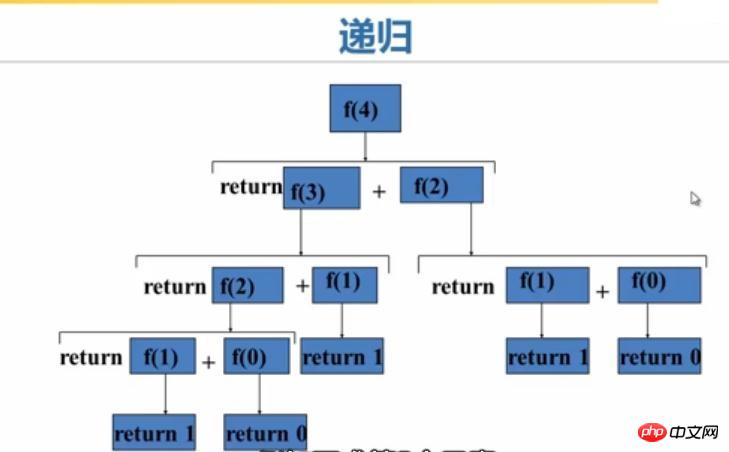
同一程序,使用递归虽然程序简洁,但递归的执行效率要比循环低,系统的资源消耗比循环大。因为递归是一层一层地往里面调用,结束后又一层一层地返回,所以递归的执行效率并不高。那为什么还要使用递归呢?因为有一些问题,我们找不到非常明显的循环方案,但容易找到明显的递归方案。比如说著名的汉诺塔问题。
2. 汉诺塔
下图是一个简化版的汉诺塔游戏,只有4个盘子:
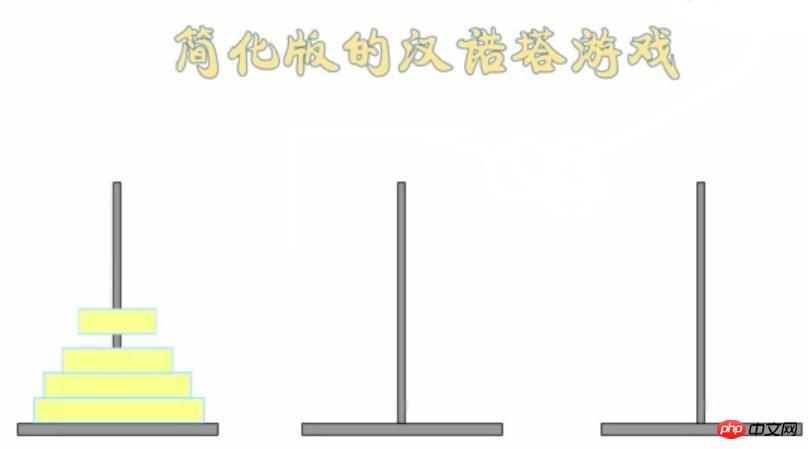
汉诺塔游戏规则如下:

python2代码如下:
def hanoi(a,b,c,n):
if n==1:#递归结束条件
print a,'->',c
else:
hanoi(a,c,b,n-1)
print a,'->',c
hanoi(b,a,c,n-1)运行结果:
>>> hanoi('A','B','C',1)
A -> C
>>> hanoi('A','B','C',2)
A -> B
A -> C
B -> C
>>> hanoi('A','B','C',3)
A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C
相关推荐:
以上是Python基于递归算法实现的汉诺塔与Fibonacci数列的详细内容。更多信息请关注PHP中文网其他相关文章!
 学习Python:2小时的每日学习是否足够?Apr 18, 2025 am 12:22 AM
学习Python:2小时的每日学习是否足够?Apr 18, 2025 am 12:22 AM每天学习Python两个小时是否足够?这取决于你的目标和学习方法。1)制定清晰的学习计划,2)选择合适的学习资源和方法,3)动手实践和复习巩固,可以在这段时间内逐步掌握Python的基本知识和高级功能。
 Web开发的Python:关键应用程序Apr 18, 2025 am 12:20 AM
Web开发的Python:关键应用程序Apr 18, 2025 am 12:20 AMPython在Web开发中的关键应用包括使用Django和Flask框架、API开发、数据分析与可视化、机器学习与AI、以及性能优化。1.Django和Flask框架:Django适合快速开发复杂应用,Flask适用于小型或高度自定义项目。2.API开发:使用Flask或DjangoRESTFramework构建RESTfulAPI。3.数据分析与可视化:利用Python处理数据并通过Web界面展示。4.机器学习与AI:Python用于构建智能Web应用。5.性能优化:通过异步编程、缓存和代码优
 Python vs.C:探索性能和效率Apr 18, 2025 am 12:20 AM
Python vs.C:探索性能和效率Apr 18, 2025 am 12:20 AMPython在开发效率上优于C ,但C 在执行性能上更高。1.Python的简洁语法和丰富库提高开发效率。2.C 的编译型特性和硬件控制提升执行性能。选择时需根据项目需求权衡开发速度与执行效率。
 python在行动中:现实世界中的例子Apr 18, 2025 am 12:18 AM
python在行动中:现实世界中的例子Apr 18, 2025 am 12:18 AMPython在现实世界中的应用包括数据分析、Web开发、人工智能和自动化。1)在数据分析中,Python使用Pandas和Matplotlib处理和可视化数据。2)Web开发中,Django和Flask框架简化了Web应用的创建。3)人工智能领域,TensorFlow和PyTorch用于构建和训练模型。4)自动化方面,Python脚本可用于复制文件等任务。
 Python的主要用途:综合概述Apr 18, 2025 am 12:18 AM
Python的主要用途:综合概述Apr 18, 2025 am 12:18 AMPython在数据科学、Web开发和自动化脚本领域广泛应用。1)在数据科学中,Python通过NumPy、Pandas等库简化数据处理和分析。2)在Web开发中,Django和Flask框架使开发者能快速构建应用。3)在自动化脚本中,Python的简洁性和标准库使其成为理想选择。
 Python的主要目的:灵活性和易用性Apr 17, 2025 am 12:14 AM
Python的主要目的:灵活性和易用性Apr 17, 2025 am 12:14 AMPython的灵活性体现在多范式支持和动态类型系统,易用性则源于语法简洁和丰富的标准库。1.灵活性:支持面向对象、函数式和过程式编程,动态类型系统提高开发效率。2.易用性:语法接近自然语言,标准库涵盖广泛功能,简化开发过程。
 Python:多功能编程的力量Apr 17, 2025 am 12:09 AM
Python:多功能编程的力量Apr 17, 2025 am 12:09 AMPython因其简洁与强大而备受青睐,适用于从初学者到高级开发者的各种需求。其多功能性体现在:1)易学易用,语法简单;2)丰富的库和框架,如NumPy、Pandas等;3)跨平台支持,可在多种操作系统上运行;4)适合脚本和自动化任务,提升工作效率。
 每天2小时学习Python:实用指南Apr 17, 2025 am 12:05 AM
每天2小时学习Python:实用指南Apr 17, 2025 am 12:05 AM可以,在每天花费两个小时的时间内学会Python。1.制定合理的学习计划,2.选择合适的学习资源,3.通过实践巩固所学知识,这些步骤能帮助你在短时间内掌握Python。


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

VSCode Windows 64位 下载
微软推出的免费、功能强大的一款IDE编辑器

螳螂BT
Mantis是一个易于部署的基于Web的缺陷跟踪工具,用于帮助产品缺陷跟踪。它需要PHP、MySQL和一个Web服务器。请查看我们的演示和托管服务。

ZendStudio 13.5.1 Mac
功能强大的PHP集成开发环境

Dreamweaver Mac版
视觉化网页开发工具

MinGW - 适用于 Windows 的极简 GNU
这个项目正在迁移到osdn.net/projects/mingw的过程中,你可以继续在那里关注我们。MinGW:GNU编译器集合(GCC)的本地Windows移植版本,可自由分发的导入库和用于构建本地Windows应用程序的头文件;包括对MSVC运行时的扩展,以支持C99功能。MinGW的所有软件都可以在64位Windows平台上运行。





