代码详解AVL树的插入

AVL树被称为高度平衡的二叉搜索树，尽量降低二叉树的高度，来保持二叉树的平衡，减少树的平均搜索长度。

AVL树的性质：1、左子树和右子树的高度之差（绝对值）不超过1

                        2、树中的每棵子树都是AVL树，

                        3、每个节点都有一个平衡因子，取值为（-1,0,1），通过平衡因子来判断树的平衡。

AVL树的插入需要考虑以下的几种情况：（箭头表示要插入的方向和节点）

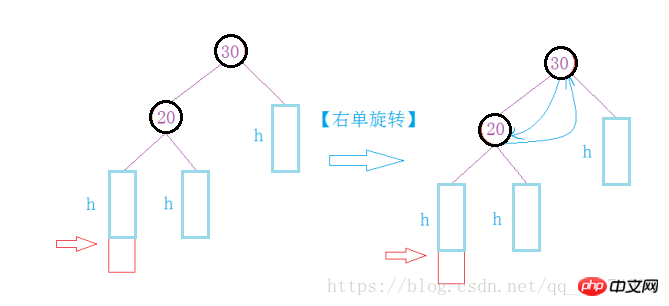
第一种情况：插入的节点在20的右边，但是这样导致10的平衡因子大于1所以需要进行旋转才能改变平衡因子

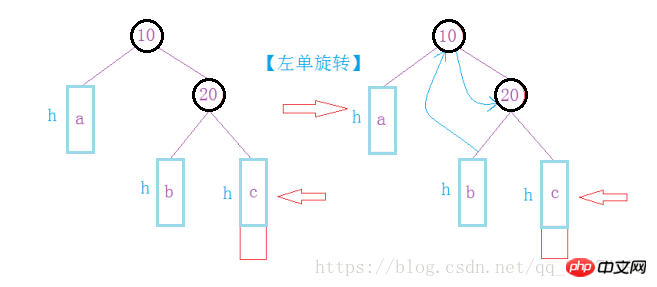
第二种情况：在左边插入，导致平衡因子也不满足条件，需要旋转

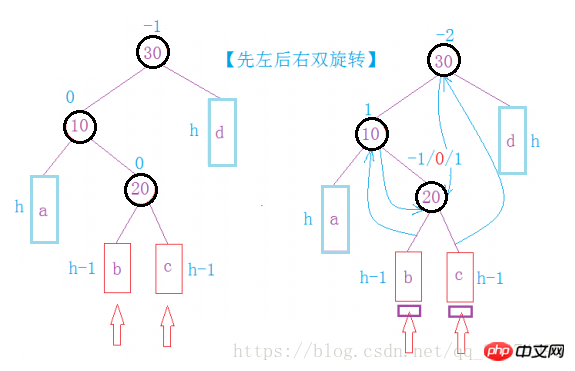
第三种情况：插入的节点可能不构成单旋，所以需要双旋来解决

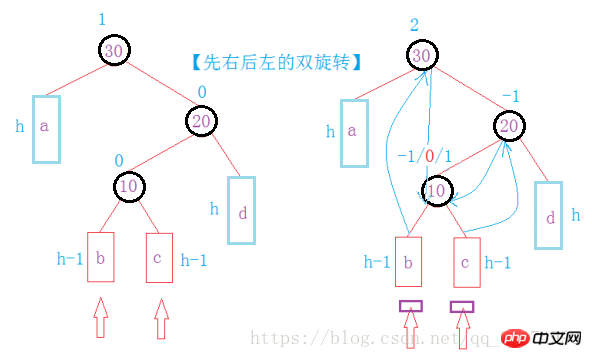
第四种情况：与第三种情况相反的双旋

如此通过旋转就可以达到在插入的时候让此二叉树达到平衡。

实现代码如下：

//main函数

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<assert.h>
using namespace std;
#include"AVLTree.h"

int main()
{
	testAVLTree();
	system("pause");
	return 0;
}

//AVLTree  ---->  被称为高度平衡的二叉搜索树
//使用三叉链来实现此二叉平衡搜索树
//性质：左右高度差不超过1 && 该树的左右子树都为二叉平衡树


template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;   
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;

	K _key;
	V _value;

	int _bf; // 平衡因子

	//构造函数
	AVLTreeNode(const K& key,const V& value) :_left(NULL), _right(NULL), _parent(NULL)
		, _key(key), _value(value), _bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
public:
	AVLTree() :_root(NULL)
	{}
	//使用非递归的插入
	bool Insert(const K& key, const V& value)
	{
		//如果根节点不存在说明插入的节点是第一个节点，直接new 一个即可
		if (_root == NULL){
			_root = new Node(key, value);
			return true;
		}
		Node* cur = _root;
		Node* parent = NULL;
		while (cur)
		{
			if (cur->_key < key){
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key>key){
				parent = cur;
				cur = cur->_left;
			}
			else{
				return false;
			}
		}
			//走到这里，说明这个节点不存在，先new
			cur = new Node(key, value);

			//比较插入节点的值与父节点的值，再考虑链上左还是右
			if (parent->_key < key){
				parent->_right = cur;
				cur->_parent = parent;
			}
			else if (parent->_key>key){
				parent->_left = cur;
				cur->_parent = parent;
			}
			else{
				while (parent)
				{
					//判断cur是插在了parent的左边还是右边，再判断平衡因子是++还是--
					if (cur == parent->_left){
						parent->_bf--;
					}
					else{
						parent->_bf++;
					}
					//++或--之后，判断平衡因子是否等于2或等于-2
					if (parent->_bf == 0)    //等于0说明没有变，则跳出循环
					{
						break;
					}
					else if (parent->_bf == 1 || parent->_bf == -1)
					{
						cur = parent;
						parent = cur->_parent;
					}
					else if (parent->_bf == 2 || parent->_bf == -2)//如果等于2或者等于-2则不再插入，先调节为二叉平衡树再插入
					{
						//根据平衡因子来判断需要调整的树是哪种类型，再选择单旋还是双旋
						//如果父节点的平衡因子等于2，说明右子树比左子树高，再判断右子树的子树是在它的左边还是右边
						if (parent->_bf == 2)
						{
							if (cur->_bf == 1){
								RotateL(parent);
							}
							else{
								RotateRL(parent);
							}
						}
						else
						{
							if (cur->_bf == -1)
								RotateR(parent);
							else
								RotateLR(parent);
						}
					}
				}
			}
			return true;
		}
		//cur = parent;
	//右单旋
	void RotateR(Node* parent)
	{
		//需要记录parent上面是否还有父亲节点
		Node* ppNode = parent->_parent;

		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		//如果subLR存在  就将它的父亲置为parent
		if (subLR)
			subLR->_parent = parent;

		subL->_right = parent;
		parent->_parent = subL;

		//如果parent等于根节点，说明已经到第一个节点，不需要调整，直接将subL作为根即可
		if (parent == _root)
		{
			_root = subL;
			subL->_parent = NULL;
		}
		else   //如果还没有到根节点还需要判断parent是左还是右
		{
			if (ppNode->_left == parent)
				ppNode->_left = subL;
			else{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
	}
	//左单旋
	void RotateL(Node* parent)
	{
		Node* ppNode = parent->_parent;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		//判断subRL是否存在
		if (subRL){
			subRL->_parent = parent;			
		}
		subR->_left = parent;
		parent->_parent = subRL;
		if (_root == parent)
		{
			_root = subR;
			subR->_parent = NULL;
		}
		else
		{
			if (ppNode->_left == parent)
				ppNode->_left = subR;
			else
				ppNode->_right = subR;
			subR->_parent = ppNode;
		}
	}
	//左右单旋
	void RotateLR(Node* parent)
	{
		RotateL(parent->_right);
		RotateR(parent);
	}
	//右左单旋
	void RotateRL(Node* parent)
	{
		RotateR(parent->_left);
		RotateL(parent);
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}	
	void _InOrder(Node* root)
	{
		if (root == NULL)
			return;
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}
	bool IsBalance()
	{
		return _IsBalance(_root);
	}
	bool _IsBalance(Node* root)
	{
		if (root == NULL)
			return;
		int leftheight = _Height(root->_left);
		int rightheight = _Height(root->_right);
		return abs(rightheight - leftheight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);
	}
	size_t _Height(Node* root)
	{
		if (root == NULL)
			return 0;
		size_t left = _Height(root->_left);
		size_t right = _Height(root->_right);
		return left > right ? left + 1 : right + 1;
	}
private:
	Node* _root;
};

void testAVLTree()
{
	AVLTree<int, int> t;
	int a[] = { 16,3,7,11,9,26,18,14,15};
	for (int i = 0; i < (sizeof(a) / sizeof(a[0])); i++)
	{
		cout<<t.Insert(a[i], 0)<<endl;
	}
	t.InOrder();
}

以上是代码详解AVL树的插入的详细内容。更多信息请关注PHP中文网其他相关文章！