解析js中0.1 + 0.2 != 0.3

Javascript中数字存储使用的是IEEE754 64位双精度浮点数

在计算机中存储为64位
1 11 52
1: 符号位 0正数 1负数
11: 指数位 用来确定范围
52: 尾数位 用来确定精度
转成十进制表示法为

num = (-1)^s * (1.f) * 2^E
E = e - 1023
s:符号位
e:指数位
f:尾数位
1023偏正值 使得指数位真实取值为[-1023, 1024] 而非 [0, 2047] 目的是为了方便比较大小
实际指数值 = 阶码 - 偏正值
阶码 = 指数的移码 - 1
移码与补码符号为互为取反
举例：
如果指数位实际值为-1
原码：100 0000 0001
反码：111 1111 1110
补码：111 1111 1111
移码：011 1111 1111
阶码：011 1111 1110 = 1022
也可以通过
阶码 = 指数 + 偏正值 = -1 + 1023 = 1022 = 011 1111 1110来计算得到

指数位全0和全1有特殊含义，在后面会讲到，用来表示+-0 和 +-∞

特殊值

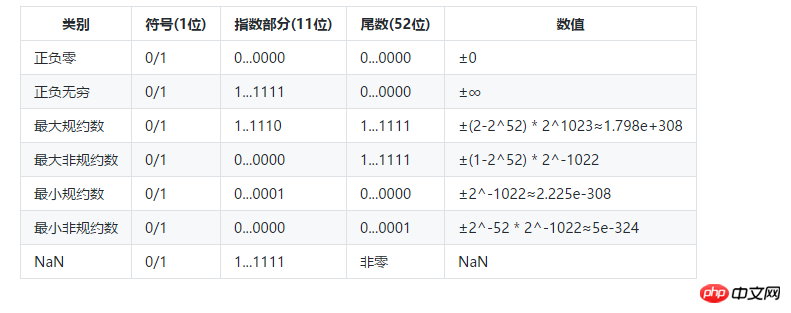
机器精度
del = 2^-52

接下来解释一下为什么在使用IEEE754标准的语言中0.1 + 0.2 = 0.30000000000000004
首先我们计算下0.1的二进制
0.1 * 2 = 0
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
....
所以0.1的二进制为 0.0001100110011001100...循环，
可以转换为2^-4 * 1.100110011001100...
由于保留位数共52位，不包括最左边整数位1，
所以最终在计算机中存储的数值是：2^-4 * 1.100 11001100 11001100 11001100 11001100 11001100 11001100 1

同理0.2
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
...
所以0.2的二进制为 0.001100110011001100...循环，
可以转换为2^-3 * 1.100110011001100...
最易最终在计算机中存储的数值是：2^-3 * 1.100 11001100 11001100 11001100 11001100 11001100 11001100 1
两者相加
0.0001100 11001100 11001100 11001100 11001100 11001100 11001100 1
+
0.001100 11001100 11001100 11001100 11001100 11001100 11001100 1
= 0.0 10011001 10011001 10011001 10011001 10011001 10011001 10011
≈ 0.30000000000000004

以上是解析js中0.1 + 0.2 != 0.3的详细内容。更多信息请关注PHP中文网其他相关文章！