JavaScript中关于 v8 排序源码的问题
- 一个新手原创
- 2017-10-24 09:57:081590浏览
JavaScript 专题系列第二十篇，也是最后一篇，解读 v8 排序源码
前言
v8 是 Chrome 的 JavaScript 引擎，其中关于数组的排序完全采用了 JavaScript 实现。
排序采用的算法跟数组的长度有关，当数组长度小于等于 10 时，采用插入排序，大于 10 的时候，采用快速排序。(当然了，这种说法并不严谨)。
我们先来看看插入排序和快速排序。
插入排序
原理
将第一个元素视为有序序列，遍历数组，将之后的元素依次插入这个构建的有序序列中。
图示
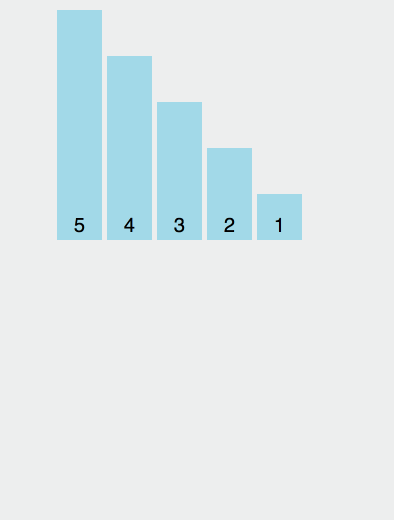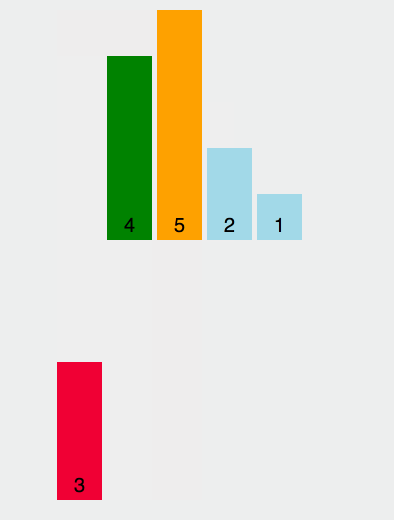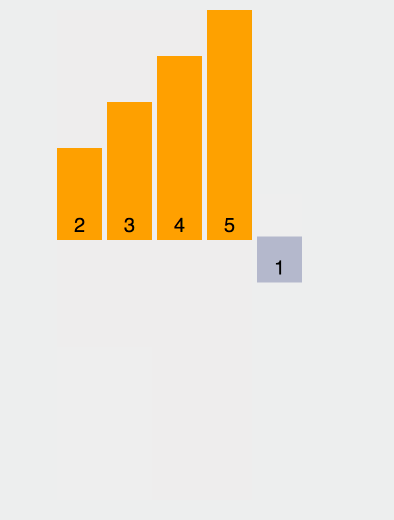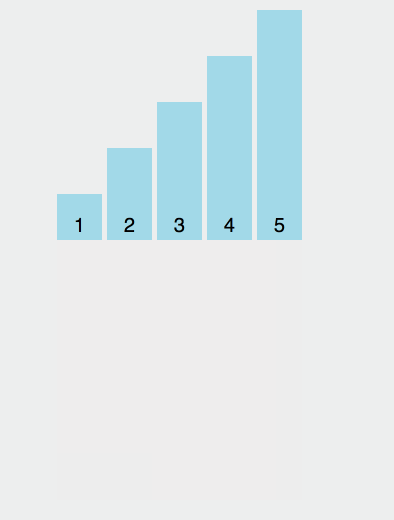
实现
function insertionSort(arr) {
for (var i = 1; i < arr.length; i++) {
var element = arr[i];
for (var j = i - 1; j >= 0; j--) {
var tmp = arr[j];
var order = tmp - element;
if (order > 0) {
arr[j + 1] = tmp;
} else {
break;
}
}
arr[j + 1] = element;
}
return arr;
}
var arr = [6, 5, 4, 3, 2, 1];
console.log(insertionSort(arr));时间复杂度
时间复杂度是指执行算法所需要的计算工作量，它考察当输入值大小趋近无穷时的情况，一般情况下，算法中基本操作重复执行的次数是问题规模 n 的某个函数。
最好情况：数组升序排列，时间复杂度为：O(n)
最坏情况：数组降序排列，时间复杂度为：O(n²)
稳定性
稳定性，是指相同的元素在排序后是否还保持相对的位置。
要注意的是对于不稳定的排序算法，只要举出一个实例，即可说明它的不稳定性；而对于稳定的排序算法，必须对算法进行分析从而得到稳定的特性。
比如 [3, 3, 1]，排序后，还是 [3, 3, 1]，但是其实是第二个 3 在 第一个 3 前，那这就是不稳定的排序算法。
插入排序是稳定的算法。
优势
当数组是快要排序好的状态或者问题规模比较小的时候，插入排序效率更高。这也是为什么 v8 会在数组长度小于等于 10 的时候采用插入排序。
快速排序
原理
选择一个元素作为"基准"
小于"基准"的元素，都移到"基准"的左边；大于"基准"的元素，都移到"基准"的右边。
对"基准"左边和右边的两个子集，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。
示例
示例和下面的实现方式来源于阮一峰老师的《快速排序（Quicksort）的Javascript实现》
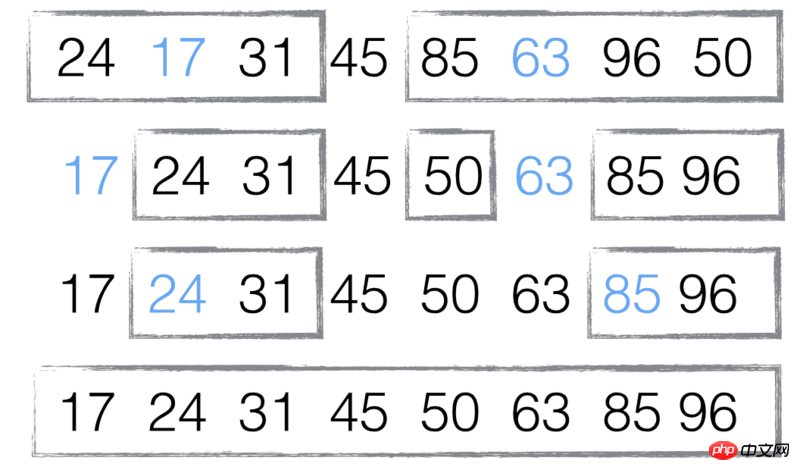
以数组 [85, 24, 63, 45, 17, 31, 96, 50] 为例：
第一步，选择中间的元素 45 作为"基准"。（基准值可以任意选择，但是选择中间的值比较容易理解。）
第二步，按照顺序，将每个元素与"基准"进行比较，形成两个子集，一个"小于45"，另一个"大于等于45"。
第三步，对两个子集不断重复第一步和第二步，直到所有子集只剩下一个元素为止。
实现
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
// 取数组的中间元素作为基准
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};然而这种实现方式需要额外的空间用来储存左右子集，所以还有一种原地(in-place)排序的实现方式。
图示
我们来看看原地排序的实现图示：
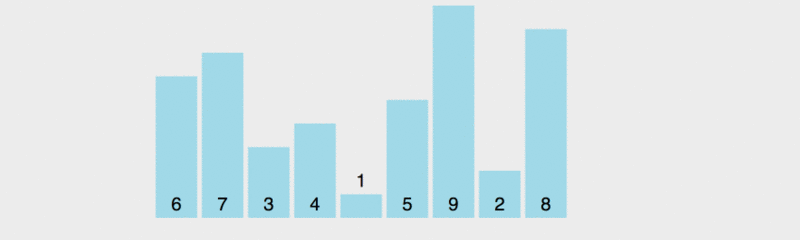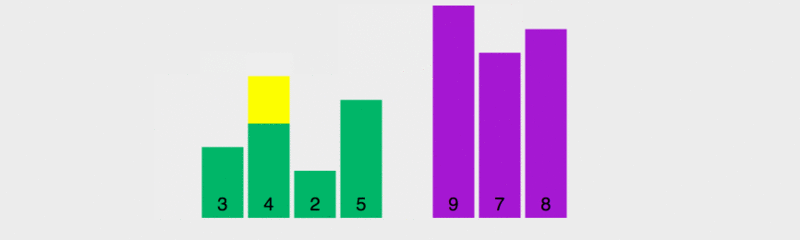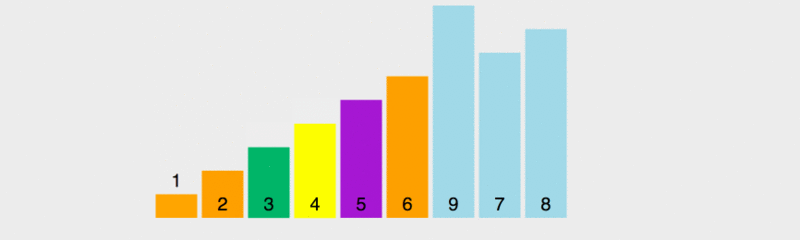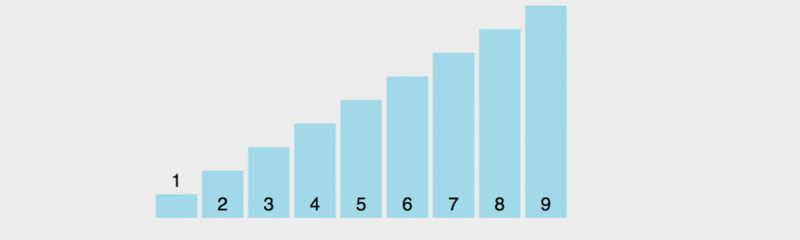
为了让大家看明白快速排序的原理，我调慢了执行速度。
在这张示意图里，基准的取值规则是取最左边的元素，黄色代表当前的基准，绿色代表小于基准的元素，紫色代表大于基准的元素。
我们会发现，绿色的元素会紧挨在基准的右边，紫色的元素会被移到后面，然后交换基准和绿色的最后一个元素，此时，基准处于正确的位置，即前面的元素都小于基准值，后面的元素都大于基准值。然后再对前面的和后面的多个元素取基准，做排序。
in-place 实现
function quickSort(arr) {
// 交换元素
function swap(arr, a, b) {
var temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
function partition(arr, left, right) {
var pivot = arr[left];
var storeIndex = left;
for (var i = left + 1; i <= right; i++) {
if (arr[i] < pivot) {
swap(arr, ++storeIndex, i);
}
}
swap(arr, left, storeIndex);
return storeIndex;
}
function sort(arr, left, right) {
if (left < right) {
var storeIndex = partition(arr, left, right);
sort(arr, left, storeIndex - 1);
sort(arr, storeIndex + 1, right);
}
}
sort(arr, 0, arr.length - 1);
return arr;
}
console.log(quickSort(6, 7, 3, 4, 1, 5, 9, 2, 8))稳定性
快速排序是不稳定的排序。如果要证明一个排序是不稳定的，你只用举出一个实例就行。
所以我们举一个呗~
就以数组 [1, 2, 3, 3, 4, 5] 为例，因为基准的选择不确定，假如选定了第三个元素(也就是第一个 3) 为基准，所有小于 3 的元素在前面，大于等于 3 的在后面，排序的结果没有问题。可是如果选择了第四个元素(也就是第二个 3 )，小于 3 的在基准前面，大于等于 3 的在基准后面，第一个 3 就会被移动到 第二个 3 后面，所以快速排序是不稳定的排序。
时间复杂度
阮一峰老师的实现中，基准取的是中间元素，而原地排序中基准取最左边的元素。快速排序的关键点就在于基准的选择，选取不同的基准时，会有不同性能表现。
快速排序的时间复杂度最好为 O(nlogn)，可是为什么是 nlogn 呢？来一个并不严谨的证明：
在最佳情况下，每一次都平分整个数组。假设数组有 n 个元素，其递归的深度就为 log2n + 1，时间复杂度为 O(n)[(log2n + 1)]，因为时间复杂度考察当输入值大小趋近无穷时的情况，所以会忽略低阶项，时间复杂度为：o(nlog2n)。
如果一个程序的运行时间是对数级的，则随着 n 的增大程序会渐渐慢下来。如果底数是 10，lg1000 等于 3，如果 n 为 1000000，lgn 等于 6，仅为之前的两倍。如果底数为 2，log21000 的值约为 10，log21000000 的值约为 19，约为之前的两倍。我们可以发现任意底数的一个对数函数其实都相差一个常数倍而已。所以我们认为 O(logn)已经可以表达所有底数的对数了，所以时间复杂度最后为： O(nlogn)。
而在最差情况下，如果对一个已经排序好的数组，每次选择基准元素时总是选择第一个元素或者最后一个元素，那么每次都会有一个子集是空的，递归的层数将达到 n，最后导致算法的时间复杂度退化为 O(n²)。
这也充分说明了一个基准的选择是多么的重要，而 v8 为了提高性能，就对基准的选择做了很多优化。
v8 基准选择
v8 选择基准的原理是从头和尾之外再选择一个元素，然后三个值排序取中间值。
当数组长度大于 10 但是小于 1000 的时候，取中间位置的元素，实现代码为：
// 基准的下标 // >> 1 相当于除以 2 (忽略余数) third_index = from + ((to - from) >> 1);
当数组长度大于 1000 的时候，每隔 200 ~ 215 个元素取一个值，然后将这些值进行排序，取中间值的下标，实现的代码为：
// 简单处理过
function GetThirdIndex(a, from, to) {
var t_array = new Array();
// & 位运算符
var increment = 200 + ((to - from) & 15);
var j = 0;
from += 1;
to -= 1;
for (var i = from; i < to; i += increment) {
t_array[j] = [i, a[i]];
j++;
}
// 对随机挑选的这些值进行排序
t_array.sort(function(a, b) {
return comparefn(a[1], b[1]);
});
// 取中间值的下标
var third_index = t_array[t_array.length >> 1][0];
return third_index;
}也许你会好奇 200 + ((to - from) & 15) 是什么意思？
& 表示是按位与，对整数操作数逐位执行布尔与操作。只有两个操作数中相对应的位都是 1，结果中的这一位才是 1。
以 15 & 127 为例：
15 二进制为： （0000 1111）
127 二进制为：（1111 1111）
按位与结果为：（0000 1111）＝ 15
所以 15 & 127 的结果为 15。
注意 15 的二进制为： 1111，这就意味着任何和 15 按位与的结果都会小于或者等于 15，这才实现了每隔 200 ~ 215 个元素取一个值。
v8 源码
终于到了看源码的时刻！源码地址为：https://github.com/v8/v8/blob/master/src/js/array.js#L758。
function InsertionSort(a, from, to) {
for (var i = from + 1; i < to; i++) {
var element = a[i];
for (var j = i - 1; j >= from; j--) {
var tmp = a[j];
var order = comparefn(tmp, element);
if (order > 0) {
a[j + 1] = tmp;
} else {
break;
}
}
a[j + 1] = element;
}
};
function QuickSort(a, from, to) {
var third_index = 0;
while (true) {
// Insertion sort is faster for short arrays.
if (to - from <= 10) {
InsertionSort(a, from, to);
return;
}
if (to - from > 1000) {
third_index = GetThirdIndex(a, from, to);
} else {
third_index = from + ((to - from) >> 1);
}
// Find a pivot as the median of first, last and middle element.
var v0 = a[from];
var v1 = a[to - 1];
var v2 = a[third_index];
var c01 = comparefn(v0, v1);
if (c01 > 0) {
// v1 < v0, so swap them.
var tmp = v0;
v0 = v1;
v1 = tmp;
} // v0 <= v1.
var c02 = comparefn(v0, v2);
if (c02 >= 0) {
// v2 <= v0 <= v1.
var tmp = v0;
v0 = v2;
v2 = v1;
v1 = tmp;
} else {
// v0 <= v1 && v0 < v2
var c12 = comparefn(v1, v2);
if (c12 > 0) {
// v0 <= v2 < v1
var tmp = v1;
v1 = v2;
v2 = tmp;
}
}
// v0 <= v1 <= v2
a[from] = v0;
a[to - 1] = v2;
var pivot = v1;
var low_end = from + 1; // Upper bound of elements lower than pivot.
var high_start = to - 1; // Lower bound of elements greater than pivot.
a[third_index] = a[low_end];
a[low_end] = pivot;
// From low_end to i are elements equal to pivot.
// From i to high_start are elements that haven&#39;t been compared yet.
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
var order = comparefn(element, pivot);
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
} else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = comparefn(top_elem, pivot);
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
}
}
if (to - high_start < low_end - from) {
QuickSort(a, high_start, to);
to = low_end;
} else {
QuickSort(a, from, low_end);
from = high_start;
}
}
}
var arr = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0];
function comparefn(a, b) {
return a - b
}
QuickSort(arr, 0, arr.length)
console.log(arr)我们以数组 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0] 为例，分析执行的过程。
1.执行 QuickSort 函数 参数 from 值为 0，参数 to 的值 11。
2.10 c7ba78f8f51b7321cde06a9f72ed98cf> 1) = 5，基准值 a[5] 为 5。
3.比较 a[0] a[10] a[5] 的值，然后根据比较结果修改数组，数组此时为 [0, 9, 8, 7, 6, 5, 4, 3, 2, 1, 10]
4.将基准值和数组的第(from + 1)个即数组的第二个元素互换，此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]，此时在基准值 5 前面的元素肯定是小于 5 的，因为第三步已经做了一次比较。后面的元素是未排序的。
我们接下来要做的就是把后面的元素中小于 5 的全部移到 5 的前面。
5.然后我们进入 partition 循环，我们依然以这个数组为例，单独抽出来写个 demo 讲一讲
// 假设代码执行到这里，为了方便演示，我们直接设置 low_end 等变量的值
// 可以直接复制到浏览器中查看数组变换效果
var a = [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]
var low_end = 1;
var high_start = 10;
var pivot = 5;
console.log(&#39;起始数组为&#39;, a)
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
console.log(&#39;循环当前的元素为：&#39;, a[i])
var order = element - pivot;
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
console.log(a)
}
else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = top_elem - pivot;
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
console.log(a)
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
console.log(a)
}
}
console.log(&#39;最后的结果为&#39;, a)
console.log(low_end)
console.log(high_start)6.此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]，循环从第三个元素开始，a[i] 的值为 8，因为大于基准值 5，即 order > 0，开始执行 do while 循环，do while 循环的目的在于倒序查找元素，找到第一个小于基准值的元素，然后让这个元素跟 a[i] 的位置交换。
第一个小于基准值的元素为 1，然后 1 与 8 交换，数组变成 [0, 5, 1, 7, 6, 9, 4, 3, 2, 8, 10]。high_start 的值是为了记录倒序查找到哪里了。
7.此时 a[i] 的值变成了 1，然后让 1 跟 基准值 5 交换，数组变成了 [0, 1, 5, 7, 6, 9, 4, 3, 2, 8, 10]，low_end 的值加 1，low_end 的值是为了记录基准值的所在位置。
8.循环接着执行，遍历第四个元素 7，跟第 6、7 的步骤一致，数组先变成 [0, 1, 5, 2, 6, 9, 4, 3, 7, 8, 10]，再变成 [0, 1, 2, 5, 6, 9, 4, 3, 7, 8, 10]
9.遍历第五个元素 6，跟第 6、7 的步骤一致，数组先变成 [0, 1, 2, 5, 3, 9, 4, 6, 7, 8, 10]，再变成 [0, 1, 2, 3, 5, 9, 4, 6, 7, 8, 10]
10.遍历第六个元素 9，跟第 6、7 的步骤一致，数组先变成 [0, 1, 2, 3, 5, 4, 9, 6, 7, 8, 10]，再变成 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]
11.在下一次遍历中，因为 i == high_start，意味着正序和倒序的查找终于找到一起了，后面的元素肯定都是大于基准值的，此时退出循环
12.遍历后的结果为 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]，在基准值 5 前面的元素都小于 5，后面的元素都大于 5，然后我们分别对两个子集进行 QuickSort
13.此时 low_end 值为 5，high_start 值为 6，to 的值依然是 10，from 的值依然是 0，to - high_start < low_end - from 的结果为 true，我们对 QuickSort(a, 6, 10)，即对后面的元素进行排序，但是注意，在新的 QuickSort 中，因为 from - to 的值小于 10，所以这一次其实是采用了插入排序。所以准确的说，当数组长度大于 10 的时候，v8 采用了快速排序和插入排序的混合排序方法。
14.然后 to = low_end 即设置 to 为 5，因为 while(true) 的原因，会再执行一遍，to - from 的值为 5，执行 InsertionSort(a, 0, 5)，即对基准值前面的元素执行一次插入排序。
15.因为在 to - from <= 10 的判断中，有 return 语句，所以 while 循环结束。
16.v8 在对数组进行了一次快速排序后，然后对两个子集分别进行了插入排序，最终修改数组为正确排序后的数组。
比较
最后来张示意图感受下插入排序和快速排序：
图片来自于 https://www.toptal.com/developers/sorting-algorithms
专题系列
JavaScript专题系列目录地址：https://github.com/mqyqingfeng/Blog。
JavaScript专题系列预计写二十篇左右，主要研究日常开发中一些功能点的实现，比如防抖、节流、去重、类型判断、拷贝、最值、扁平、柯里、递归、乱序、排序等，特点是研(chao)究(xi) underscore 和 jQuery 的实现方式。
以上是JavaScript中关于 v8 排序源码的问题的详细内容。更多信息请关注PHP中文网其他相关文章！