PHP实现的迪科斯彻最短路径

这篇文章主要介绍了PHP实现的迪科斯彻(Dijkstra)最短路径算法,简单描述了迪科斯彻(Dijkstra)最短路径算法的概念、功能并结合具体实例形式分析了php实现迪科斯彻(Dijkstra)最短路径算法的相关步骤与操作技巧,需要的朋友可以参考下

本文实例讲述了PHP实现的迪科斯彻(Dijkstra)最短路径算法。分享给大家供大家参考，具体如下：

一、待解决问题

单源最短路径问题，在给定有向图中求一个顶点（单源顶点）到其他所有顶点的最短路径问题。在下图中，每条边上有一个权值，希望求解A到所有其他顶点（B/C/D/E/F/G）的最短路径。

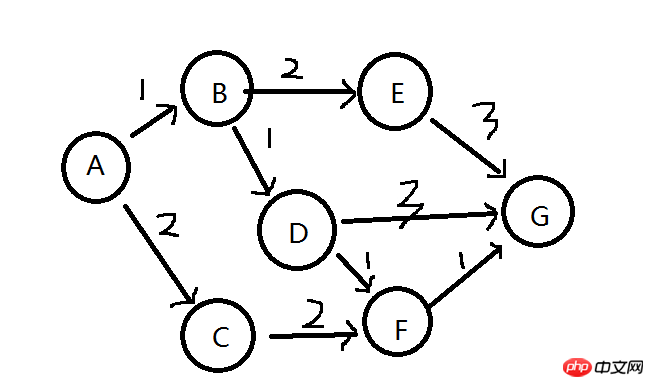
二、问题分析（最短路径的子结构同样最优性）

如果P（A,G）是从顶点A到G的最短路径,假设D和F是这条路径上的中间点，那么P(D,F)一定时从D到F的最短路径。如果P(D,F)不是D到F的最短路径，那必然存在某一个节点M的另一条D到F的路径可以使P(A,B...M...F,G)比P(A,G)小，自相矛盾。

有了这样的性质，我们可以了解Dijkstra算法。

三、Dijkstra算法

Dijkstra 算法，又叫迪科斯彻算法（Dijkstra），又称为单源最短路径算法，所谓单源是在一个有向图中，从一个顶点出发，求该顶点至所有可到达顶点的最短路径问题。 问题描述为设G=（V，E）是一个有向图，V表示顶点，E表示边。它的每一条边（i，j）属于E，都有一个非负权W（I,j），在G中指定一个结点v0，要求把从v0到G的每一个接vj（vj属于V）的最短有向路径找出来（或者指出不存在）。 Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离。

Dijkstra的贪心应用在他利用（二）中的性质，不断地选取“最近”的节点并试探每个节点的所有可能存在链接，以起始点为中心向外层层扩展，直到扩展到终点为止。对于源点A，逐步扩展，根据dist[j]=min{dist[j],dist[i]+matrix[i][j]}更新与i直接相邻的顶点信息。

算法描述

1)算法思想：

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则de9b834b22c2c30d5bc5e894bb9e7727正常有权值，若u不是v的出边邻接点，则de9b834b22c2c30d5bc5e894bb9e7727权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中与k相邻的各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值为顶点k的距离加上k与u边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

四、算法PHP实现

<?php
class Dijkstra
{
  private $G;
  public function __construct()
  {
    //有向图存储
    $this->G = array(
      array(0,1,2,0,0,0,0),
      array(0,0,0,1,2,0,0),
      array(0,0,0,0,0,2,0),
      array(0,0,0,0,0,1,3),
      array(0,0,0,0,0,0,3),
      array(0,0,0,0,0,0,1),
      array(0,0,0,0,0,0,0),
    );
  }
  public function calculate()
  {
    // 存储已经选择节点和剩余节点
    $U = array(0);
    $V = array(1,2,3,4,5,6);
    // 存储路径上节点距离源点的最小距离
    $d = array();
    //初始化图中节点与源点0的最小距离
    for($i=1;$i<7;$i++)
    {
      if($this->G[0][$i]>0)
      {
        $d[$i] = $this->G[0][$i];
      }
      else
      {
        $d[$i] = 1000000;
      }
    }
    // n-1次循环完成转移节点任务
    for($l=0;$l<6;$l++)
    {
      // 查找剩余节点中距离源点最近的节点v
      $current_min = 100000;
      $current_min_v = 0;
      foreach($V as $k=>$v)
      {
        if($d[$v] < $current_min)
        {
          $current_min = $d[$v];
          $current_min_v = $v;
        }
      }
      //从V中更新顶点到U中
      array_push($U,$current_min_v);
      array_splice($V,array_search($current_min_v,$V),1);
      //更新
      foreach($V as $k=>$u)
      {
        if($this->G[$current_min_v][$u]!=0&&$d[$u]>$d[$current_min_v]+$this->G[$current_min_v][$u])
        {
          $d[$u] = $d[$current_min_v]+$this->G[$current_min_v][$u];
        }
      }
    }
    foreach($d as $k => $u)
    {
      echo $k.&#39;=>&#39;.$u.&#39;<br>&#39;;
    }
  }
}
?>

调用类：

$D = new Dijkstra;
$D->calculate();

执行结果：

1=>1
2=>2
3=>2
4=>3
5=>3
6=>4

以上是PHP实现的迪科斯彻最短路径的详细内容。更多信息请关注PHP中文网其他相关文章！