SPFA算法使用教程

适用范围：给定的图存在负权边，这时类似Dijkstra等算法便没有了用武之地，而Bellman-Ford算法的复杂度又过高，SPFA算法便 派上用场了。 我们约定有向加权图G不存在负权回路，即最短路径一定存在。当然，我们可以在执行该算法前做一次拓扑排序，以判断是否存在负权回路，但这不是我们讨论的重 点。

算法思想：我们用数组d记录每个结点的最短路径估计值，用邻接表来存储图G。我们采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的 结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在 当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止

 

期望的时间复杂度O(ke)， 其中k为所有顶点进队的平均次数，可以证明k一般小于等于2。

 

实现方法：

　　建立一个队列，初始时队列里只有起始点，再建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为 0）。然后执行松弛操作，用队列里有的点作为起始点去刷新到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列 为空。

判断有无负环：
　　如果某个点进入队列的次数超过N次则存在负环（SPFA无法处理带负环的图）

 

 

 

 

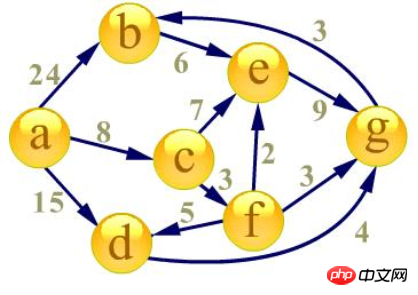
首先建立起始点a到其余各点的
最短路径表格

                                  

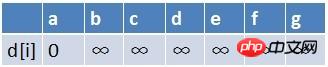
首先源点a入队，当队列非空时：
　１、队首元素（a）出队，对以a为起始点的所有边的终点依次进行松弛操作（此处有b,c,d三个点），此时路径表格状态为：

                                  

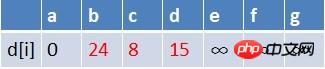
在松弛时三个点的最短路径估值变小了，而这些点队列中都没有出现，这些点
需要入队，此时，队列中新入队了三个结点b,c,d

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e点），此时路径表格状态为：

                                 

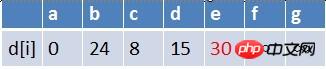
在最短路径表中，e的最短路径估值也变小了，e在队列中不存在，因此e也要
入队，此时队列中的元素为c，d，e

队首元素c点出队，对以c为起始点的所有边的终点依次进行松弛操作（此处有e,f两个点），此时路径表格状态为：

                                 

在最短路径表中，e，f的最短路径估值变小了，e在队列中存在，f不存在。因此
e不用入队了，f要入队，此时队列中的元素为d，e，f

 队首元素d点出队，对以d为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

 

 

                               

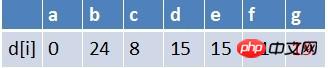
在最短路径表中，g的最短路径估值没有变小（松弛不成功），没有新结点入队，队列中元素为f，g

队首元素f点出队，对以f为起始点的所有边的终点依次进行松弛操作（此处有d，e，g三个点），此时路径表格状态为：

                               

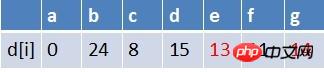
在最短路径表中，e，g的最短路径估值又变小，队列中无e点，e入队，队列中存在g这个点，g不用入队，此时队列中元素为g，e

队首元素g点出队，对以g为起始点的所有边的终点依次进行松弛操作（此处只有b点），此时路径表格状态为：

                           

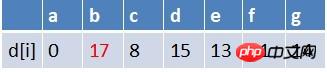
在最短路径表中，b的最短路径估值又变小，队列中无b点，b入队，此时队列中元素为e，b
队首元素e点出队，对以e为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

 

                          

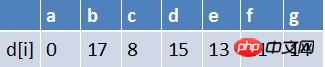
在最短路径表中，g的最短路径估值没变化（松弛不成功），此时队列中元素为b

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e这个点），此时路径表格状态为：

                         

在最短路径表中，e的最短路径估值没变化（松弛不成功），此时队列为空了

最终a到g的最短路径为１４

 

java代码

package spfa负权路径;

import java.awt.List;
import java.util.ArrayList;
import java.util.Scanner;
public class SPFA {
	/**
	 * @param args
	 */
	public long[] result;         //用于得到第s个顶点到其它顶点之间的最短距离
	//数组实现邻接表存储
	class edge{
		public int a;//边的起点
		public int b;//边的终点
		public int value;//边的值
		public edge(int a,int b,int value){
			this.a=a;
			this.b=b;
			this.value=value;
		}
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		SPFA spafa=new SPFA();
		Scanner scan=new Scanner(System.in);
		int n=scan.nextInt();
		int s=scan.nextInt();
		int p=scan.nextInt();
		edge[] A=new edge[p];
		for(int i=0;i<p;i++){
			int a=scan.nextInt();
			int b=scan.nextInt();
			int value=scan.nextInt();
			A[i]=spafa.new edge(a,b,value);
		}
		if(spafa.getShortestPaths(n,s,A)){
			for(int i=0;i<spafa.result.length;i++){
				System.out.println(spafa.result[i]+" ");
			}
		}else{
			System.out.println("存在负环");
		}
	}
	/*
     * 参数n:给定图的顶点个数
     * 参数s:求取第s个顶点到其它所有顶点之间的最短距离
     * 参数edge:给定图的具体边
     * 函数功能：如果给定图不含负权回路，则可以得到最终结果，如果含有负权回路，则不能得到最终结果
     */
	private boolean getShortestPaths(int n, int s, edge[] A) {
		// TODO Auto-generated method stub
		ArrayList<Integer> list = new ArrayList<Integer>();
		result=new long[n];
		boolean used[]=new boolean[n];
		int num[]=new int[n];
		for(int i=0;i<n;i++){
			result[i]=Integer.MAX_VALUE;
			used[i]=false;
		}
		result[s]=0;//第s个顶点到自身距离为0
		used[s]=true;//表示第s个顶点进入数组队
		num[s]=1;//表示第s个顶点已被遍历一次
		list.add(s); //第s个顶点入队
		while(list.size()!=0){
			int a=list.get(0);//获取数组队中第一个元素
			list.remove(0);//删除数组队中第一个元素
			for(int i=0;i<A.length;i++){
			//当list数组队的第一个元素等于边A[i]的起点时
				if(a==A[i].a&&result[A[i].b]>(result[A[i].a]+A[i].value)){
					result[A[i].b]=result[A[i].a]+A[i].value;
					if(!used[A[i].b]){
						list.add(A[i].b);
						num[A[i].b]++;
						if(num[A[i].b]>n){
							return false;
						}
						used[A[i].b]=true;//表示边A[i]的终点b已进入数组队
					}
				}
			}
			used[a]=false; //顶点a出数组对
		}
		return true;
	}
}

　　

以上是SPFA算法使用教程的详细内容。更多信息请关注PHP中文网其他相关文章！