给定一个n * n的二维数组,使用螺旋矩阵算法,遍历它,并返回路径。
例子如下:
array = [[1,2,3],
[4,5,6],
[7,8,9]]
snail(array) // => [1,2,3,6,9,8,7,4,5]这个程序的例子可能不太直观,那就上个图来展示下它这个过程。
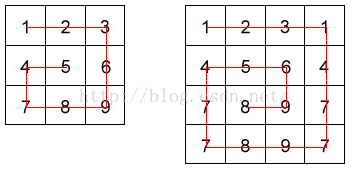
大家可以看到,就好比一个人在迷宫里面前进,它首先位于(0,0)这个位置,接着向右走,遇到边界,就改为向下走,又遇到了边界,改为向左走....
细心的人,很快就可以发现一个规律:
迷宫里的这个人有四种基本行进策略。
1.当向右走,如果遇到边界,或者右边的格子已经走过,那么就向下走,否则继续向右走。
2.当向下走,如果遇到边界,或者下边的格子已经走过,那么就向左走,否则继续向下走。
3.当向左走,如果遇到边界,或者左边的格子已经走过,那么就向上走,否则继续向左走。
4.当向上走,如果遇到边界,或者上边的格子已经走过,那么就向右走,否则继续向上走。
大家可以看出来,这是一个递归的过程,那么,何时终止呢?
当每一个格子,这个人都访问过了时,那么就终止了。
我下面写的程序,用到了一个boolean类型的二维数组,记录格子是否已经走过。
引入了上下左右四种函数,分别表示四种策略。
function snail(array) {
//当前行
var row = 0;
//当前列
var col = 0;
//对应的存放boolean值的二维数组
var hasVisited = [];
//存放结果的数组
var result = [];
//数组元素个数
var size = array.length * array[0].length;
//boolean二维数组初始化
for (var i = 0; i < array.length; i++) {
var temp = [];
var len = array[i].length;
for (var j = 0; j < len; j++) {
temp.push(false);
}
hasVisited.push(temp);
}
function right() {
if (result.length < size) {
result.push(array[row][col]);
hasVisited[row][col] = true;
if (col + 1 >= array.length || hasVisited[row][col + 1]) {
row += 1;
down();
} else {
col += 1;
right();
}
}
}
function down() {
if (result.length < size) {
result.push(array[row][col]);
hasVisited[row][col] = true;
if (row + 1 >= array.length || hasVisited[row + 1][col]) {
col -= 1;
left();
} else {
row += 1;
down();
}
}
}
function left() {
if (result.length < size) {
result.push(array[row][col]);
hasVisited[row][col] = true;
if (col == 0 || hasVisited[row][col - 1]) {
row -= 1;
up();
} else {
col -= 1;
left();
}
}
}
function up() {
if (result.length < size) {
result.push(array[row][col]);
hasVisited[row][col] = true;
if (hasVisited[row - 1][col]) {
col += 1;
right();
} else {
row -= 1;
up();
}
}
}
//首先往右走
right();
return result;
}以上就是JavaScript趣题:螺旋矩阵的内容,更多相关内容请关注PHP中文网(www.php.cn)!
 JavaScript的角色:使网络交互和动态Apr 24, 2025 am 12:12 AM
JavaScript的角色:使网络交互和动态Apr 24, 2025 am 12:12 AMJavaScript是现代网站的核心,因为它增强了网页的交互性和动态性。1)它允许在不刷新页面的情况下改变内容,2)通过DOMAPI操作网页,3)支持复杂的交互效果如动画和拖放,4)优化性能和最佳实践提高用户体验。
 C和JavaScript:连接解释Apr 23, 2025 am 12:07 AM
C和JavaScript:连接解释Apr 23, 2025 am 12:07 AMC 和JavaScript通过WebAssembly实现互操作性。1)C 代码编译成WebAssembly模块,引入到JavaScript环境中,增强计算能力。2)在游戏开发中,C 处理物理引擎和图形渲染,JavaScript负责游戏逻辑和用户界面。
 从网站到应用程序:JavaScript的不同应用Apr 22, 2025 am 12:02 AM
从网站到应用程序:JavaScript的不同应用Apr 22, 2025 am 12:02 AMJavaScript在网站、移动应用、桌面应用和服务器端编程中均有广泛应用。1)在网站开发中,JavaScript与HTML、CSS一起操作DOM,实现动态效果,并支持如jQuery、React等框架。2)通过ReactNative和Ionic,JavaScript用于开发跨平台移动应用。3)Electron框架使JavaScript能构建桌面应用。4)Node.js让JavaScript在服务器端运行,支持高并发请求。
 Python vs. JavaScript:比较用例和应用程序Apr 21, 2025 am 12:01 AM
Python vs. JavaScript:比较用例和应用程序Apr 21, 2025 am 12:01 AMPython更适合数据科学和自动化,JavaScript更适合前端和全栈开发。1.Python在数据科学和机器学习中表现出色,使用NumPy、Pandas等库进行数据处理和建模。2.Python在自动化和脚本编写方面简洁高效。3.JavaScript在前端开发中不可或缺,用于构建动态网页和单页面应用。4.JavaScript通过Node.js在后端开发中发挥作用,支持全栈开发。
 C/C在JavaScript口译员和编译器中的作用Apr 20, 2025 am 12:01 AM
C/C在JavaScript口译员和编译器中的作用Apr 20, 2025 am 12:01 AMC和C 在JavaScript引擎中扮演了至关重要的角色,主要用于实现解释器和JIT编译器。 1)C 用于解析JavaScript源码并生成抽象语法树。 2)C 负责生成和执行字节码。 3)C 实现JIT编译器,在运行时优化和编译热点代码,显着提高JavaScript的执行效率。
 JavaScript在行动中:现实世界中的示例和项目Apr 19, 2025 am 12:13 AM
JavaScript在行动中:现实世界中的示例和项目Apr 19, 2025 am 12:13 AMJavaScript在现实世界中的应用包括前端和后端开发。1)通过构建TODO列表应用展示前端应用,涉及DOM操作和事件处理。2)通过Node.js和Express构建RESTfulAPI展示后端应用。
 JavaScript和Web:核心功能和用例Apr 18, 2025 am 12:19 AM
JavaScript和Web:核心功能和用例Apr 18, 2025 am 12:19 AMJavaScript在Web开发中的主要用途包括客户端交互、表单验证和异步通信。1)通过DOM操作实现动态内容更新和用户交互;2)在用户提交数据前进行客户端验证,提高用户体验;3)通过AJAX技术实现与服务器的无刷新通信。
 了解JavaScript引擎:实施详细信息Apr 17, 2025 am 12:05 AM
了解JavaScript引擎:实施详细信息Apr 17, 2025 am 12:05 AM理解JavaScript引擎内部工作原理对开发者重要,因为它能帮助编写更高效的代码并理解性能瓶颈和优化策略。1)引擎的工作流程包括解析、编译和执行三个阶段;2)执行过程中,引擎会进行动态优化,如内联缓存和隐藏类;3)最佳实践包括避免全局变量、优化循环、使用const和let,以及避免过度使用闭包。


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

SecLists
SecLists是最终安全测试人员的伙伴。它是一个包含各种类型列表的集合,这些列表在安全评估过程中经常使用,都在一个地方。SecLists通过方便地提供安全测试人员可能需要的所有列表,帮助提高安全测试的效率和生产力。列表类型包括用户名、密码、URL、模糊测试有效载荷、敏感数据模式、Web shell等等。测试人员只需将此存储库拉到新的测试机上,他就可以访问到所需的每种类型的列表。

PhpStorm Mac 版本
最新(2018.2.1 )专业的PHP集成开发工具

WebStorm Mac版
好用的JavaScript开发工具

记事本++7.3.1
好用且免费的代码编辑器

DVWA
Damn Vulnerable Web App (DVWA) 是一个PHP/MySQL的Web应用程序,非常容易受到攻击。它的主要目标是成为安全专业人员在合法环境中测试自己的技能和工具的辅助工具,帮助Web开发人员更好地理解保护Web应用程序的过程,并帮助教师/学生在课堂环境中教授/学习Web应用程序安全。DVWA的目标是通过简单直接的界面练习一些最常见的Web漏洞,难度各不相同。请注意,该软件中





