详解C#的排列组合

排列组合的概念

排列：从n个不同元素中取出m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个元素中取出m个元素的一个排列(Arrangement)。

组合：从m个不同的元素中，任取n（n≤m）个元素为一组，叫作从m个不同元素中取出n个元素的一个组合。

排列组合实现代码

上一个项目做的一个水路的路径规划时，用到了排列的数据结构。求任意N个点里M个点的不同顺序的组合个数。

这样求最优路径。下面贴一段不知道哪里找的排列组合的算法。

public class PermutationAndCombination<T>
 {
 /// <summary>
 /// 交换两个变量
 /// </summary>
 /// <param name="a">变量1</param>
 /// <param name="b">变量2</param>
 public static void Swap(ref T a, ref T b)
 {
 T temp = a;
 a = b;
 b = temp;
 }
 /// <summary>
 /// 递归算法求数组的组合(私有成员)
 /// </summary>
 /// <param name="list">返回的范型</param>
 /// <param name="t">所求数组</param>
 /// <param name="n">辅助变量</param>
 /// <param name="m">辅助变量</param>
 /// <param name="b">辅助数组</param>
 /// <param name="M">辅助变量M</param>
 private static void GetCombination(ref List<T[]> list, T[] t, int n, int m, int[] b, int M)
 {
 for (int i = n; i >= m; i--)
 {
 b[m - 1] = i - 1;
 if (m > 1)
 {
 GetCombination(ref list, t, i - 1, m - 1, b, M);
 }
 else
 {
 if (list == null)
 {
 list = new List<T[]>();
 }
 T[] temp = new T[M];
 for (int j = 0; j < b.Length; j++)
 {
 temp[j] = t[b[j]];
 }
 list.Add(temp);
 }
 }
 }
 /// <summary>
 /// 递归算法求排列(私有成员)
 /// </summary>
 /// <param name="list">返回的列表</param>
 /// <param name="t">所求数组</param>
 /// <param name="startIndex">起始标号</param>
 /// <param name="endIndex">结束标号</param>
 private static void GetPermutation(ref List<T[]> list, T[] t, int startIndex, int endIndex)
 {
 if (startIndex == endIndex)
 {
 if (list == null)
 {
 list = new List<T[]>();
 }
 T[] temp = new T[t.Length];
 t.CopyTo(temp, 0);
 list.Add(temp);
 }
 else
 {
 for (int i = startIndex; i <= endIndex; i++)
 {
 Swap(ref t[startIndex], ref t[i]);
 GetPermutation(ref list, t, startIndex + 1, endIndex);
 Swap(ref t[startIndex], ref t[i]);
 }
 }
 }
 /// <summary>
 /// 求从起始标号到结束标号的排列，其余元素不变
 /// </summary>
 /// <param name="t">所求数组</param>
 /// <param name="startIndex">起始标号</param>
 /// <param name="endIndex">结束标号</param>
 /// <returns>从起始标号到结束标号排列的范型</returns>
 public static List<T[]> GetPermutation(T[] t, int startIndex, int endIndex)
 {
 if (startIndex < 0 || endIndex > t.Length - 1)
 {
 return null;
 }
 List<T[]> list = new List<T[]>();
 GetPermutation(ref list, t, startIndex, endIndex);
 return list;
 }
 /// <summary>
 /// 返回数组所有元素的全排列
 /// </summary>
 /// <param name="t">所求数组</param>
 /// <returns>全排列的范型</returns>
 public static List<T[]> GetPermutation(T[] t)
 {
 return GetPermutation(t, 0, t.Length - 1);
 }
 /// <summary>
 /// 求数组中n个元素的排列
 /// </summary>
 /// <param name="t">所求数组</param>
 /// <param name="n">元素个数</param>
 /// <returns>数组中n个元素的排列</returns>
 public static List<T[]> GetPermutation(T[] t, int n)
 {
 if (n > t.Length)
 {
 return null;
 }
 List<T[]> list = new List<T[]>();
 List<T[]> c = GetCombination(t, n);
 for (int i = 0; i < c.Count; i++)
 {
 List<T[]> l = new List<T[]>();
 GetPermutation(ref l, c[i], 0, n - 1);
 list.AddRange(l);
 }
 return list;
 }
 /// <summary>
 /// 求数组中n个元素的组合
 /// </summary>
 /// <param name="t">所求数组</param>
 /// <param name="n">元素个数</param>
 /// <returns>数组中n个元素的组合的范型</returns>
 public static List<T[]> GetCombination(T[] t, int n)
 {
 if (t.Length < n)
 {
 return null;
 }
 int[] temp = new int[n];
 List<T[]> list = new List<T[]>();
 GetCombination(ref list, t, t.Length, n, temp, n);
 return list;
 }
 }

   

  求组合：求5个数里任意3个数的组合

static void Main(string[] args)
{
int[] IntArr = new int[] { 1, 2, 3, 4, 5 }; //整型数组
List<int[]> ListCombination = PermutationAndCombination<int>.GetCombination(IntArr, 3); //求全部的3-3组合
foreach(int[] arr in ListCombination)
{
foreach(int item in arr)
{
Console.Write(item + " ");
}
Console.WriteLine("");
}
Console.ReadKey();
}

   

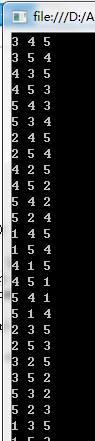
求排列：5个数取3个的任意排列

i

nt[] IntArr = new int[] { 1, 2, 3, 4, 5 }; //整型数组
List<int[]> ListCombination = PermutationAndCombination<int>.GetPermutation(IntArr, 3); //求全部的5取3排列
foreach(int[] arr in ListCombination)
{
foreach(int item in arr)
{
Console.Write(item + " ");
}
Console.WriteLine("");
}

以上就是详解C#的排列组合的内容，更多相关文章请关注PHP中文网（www.php.cn）！