介绍
回溯算法是一种有力的解决问题的技术,可以逐步构建候选解决方案。这是计算机科学中广泛使用的方法,在丢弃任何潜在的失败策略之前,系统地探索了所有可能的途径。这种方法特别适合难题,路径和约束满意度问题。掌握回溯可显着增强解决问题的能力。

关键学习目标
本指南将涵盖:
- 掌握回溯算法的基本概念。
- 应用回溯以解决组合挑战。
- 识别此技术的现实应用。
- 在编码练习中实施回溯解决方案。
- 认识到使用回溯的局限性和潜在困难。
目录
- 什么是回溯?
- 回溯如何功能?
- 编码回溯解决方案
- 回溯的最佳用例
- 通过回溯解决Sudoku
- 回溯的实际应用
- 挑战和局限性
- 常见问题
什么是回溯?
回溯是一种算法方法,它迭代地构建了候选解决方案。如果候选人被证明是无效的,则算法“回溯”到上一步并探索替代选项。这个过程一直持续到找到有效的解决方案或所有可能性耗尽。
回溯如何功能?
回溯是一种决策算法,它系统地探索了可能性,逆转了导致不可行的国家的决策。这是深度优先搜索的一种形式,在必要时逐步构建解决方案和缩回步骤。

递归探索和决策
该算法从初始状态开始,在每个步骤中做出选择。每个选择都添加到当前解决方案中,并检查算法是否违反约束。
约束验证和回溯
如果满足约束,则算法将继续;否则,它回溯,取消了最后的选择并尝试替代方案。这样可以确保详尽的探索而不会被困在无效的路径中。
解决方案验证和终止
当找到有效解决方案或探索所有可能性时,该算法将终止。
另请阅读:AI中的水壶问题是什么?
编码回溯解决方案
这是一个Python示例,展示了N-Queens问题的回溯:

DEF IS_SAFE(董事会,行,Col):
#在列中检查女王冲突,左对角线和右角
对于我的范围(行):
如果板[i] [col] =='q'或(col-i-1> = 0,并且板[row-i-1] [col-i-1] =='q')或(col I 1 <len i><p></p>
<h2 id="回溯的最佳用例">回溯的最佳用例</h2>
<p></p>
<p>让我们检查一下回溯的场景。</p>
<p></p>
<h3 id="基于约束的搜索问题">基于约束的搜索问题</h3>
<p></p>
<p>在遵守特定约束的同时,回溯在需要详尽的搜索的情况下出色。例如,在sudoku中,数字必须在行,列和3x3子格里德术中唯一。回溯通过复制不正确的位置来有效处理约束违规。</p>
<p></p>
<h3 id="组合问题解决">组合问题解决</h3>
<p></p>
<p>当生成所有排列或组合时,回溯系统会探索可能性。八个皇后区的问题,将八个女王放在棋盘上而没有相互威胁,完美地说明了此应用程序。</p>
<p></p>
<h3 id="优化问题解决">优化问题解决</h3>
<p></p>
<p>回溯对优化问题很有用,在满足约束时必须找到许多最佳选择。背包问题(选择项目以在重量限制内最大化价值),从回溯的系统探索和约束检查中获得了依赖。</p>
<p></p>
<h3 id="探路和迷宫导航">探路和迷宫导航</h3>
<p></p>
<p>回溯有效地在有障碍物的空间中导航。在迷宫求解中,该算法探索路径,从死端回溯以找到解决方案路径。</p>
<p></p>
<h3 id="模式匹配和弦操作">模式匹配和弦操作</h3>
<p></p>
<p>回溯对于诸如正则表达式匹配之类的任务很有价值,它可以系统地检查与字符串的不同模式匹配的可能性。</p>
<p></p>
<h3 id="游戏策略和决策">游戏策略和决策</h3>
<p></p>
<p>在游戏玩法中,回溯可以探索不同的移动序列,评估潜在结果并撤回失败的策略。</p>
<p></p>
<h2 id="通过回溯解决Sudoku">通过回溯解决Sudoku</h2>
<p></p>
<p> Sudoku是一个数字放置难题,是一个经典的回溯问题。</p>
<p></p>
<h4 id="算法分解">算法分解</h4>
<p></p>
<p>回溯Sudoku求解器遵循以下步骤:</p>
<pre class="brush:php;toolbar:false"> <code>1. **Locate Empty Cell:** Find the next empty cell (represented by 0). 2. **Try Numbers:** Attempt to place numbers 1-9 in the empty cell. 3. **Validate Placement:** Check if the placement is valid (no conflicts in row, column, or 3x3 subgrid). 4. **Recursive Call:** If valid, recursively call the solver to continue filling the grid. 5. **Backtrack:** If the recursive call fails (dead end), remove the number and try the next. 6. **Termination:** The algorithm stops when the grid is full or all possibilities are exhausted.</code>
验证功能
DEF IS_VALID(董事会,行,Col,Num):
#检查行,列和3x3子网格是否需要冲突
#...(像以前一样实施)
sudoku求解器功能
def solve_sudoku(董事会):
#查找空单元,尝试数字,验证,重新浏览,回溯
#...(像以前一样实施)
示例和解决方案
#示例板(0是空单元格)
sudoku_board = [
[5、3、0、0、7、0、0、0、0、0],
#...(董事会的其余部分)
这是给出的
#解决并打印解决方案
#...(像以前一样实施)
回溯的应用
回溯到不同领域的应用程序:
- 约束满意度问题(CSP): sudoku,填字游戏,地图着色。
- 组合优化:背包问题,旅行推销员问题(近似)。
- 人工智能(AI):游戏游戏(国际象棋,跳棋),计划。
- 运营研究:调度,资源分配。
- 生物信息学:序列比对。
挑战和局限性
虽然强大,但回溯有局限性:
- 指数复杂性:所需的时间可以随着问题大小而呈指数增长。
- 在某些情况下,效率低下:其他算法对于特定问题可能更有效。
- 修剪困难:有效消除非生产性路径可能具有挑战性。
- 记忆使用:深层递归会导致高度的内存消耗。
- 顺序性质:难以有效地平行。
- 实施复杂性:对于复杂的问题,可以正确实施很复杂。
结论
回溯是一种通过系统地探索可能性并丢弃不可行的解决方案来解决问题的多功能算法。尽管其指数时间复杂性可能是一个限制,但它在解决复杂组合问题方面的有效性使其成为程序员武器库中的宝贵工具。
常见问题
Q1:什么是算法中的回溯?答:递归解决问题的技术,探讨了所有潜在的解决方案,放弃了毫无主张的路径。
Q2:回溯的常见应用?答:Sudoku,N-Queens,迷宫解决,约束满意度问题。
Q3:回溯始终有效吗?答:不,它的指数时间复杂性可以使其对于大问题效率低下。
问题4:回溯与蛮力有何不同?答:回溯前进的路径毫无意义,而蛮力则尝试所有可能性。
Q5:回溯能否确保最佳解决方案?答:不一定;它找到了一个解决方案,但并非总是最好的解决方案。
以上是回溯算法的综合指南的详细内容。更多信息请关注PHP中文网其他相关文章!
 AI动作人物趋势,解释 - 以及如何制作自己的Apr 16, 2025 am 11:22 AM
AI动作人物趋势,解释 - 以及如何制作自己的Apr 16, 2025 am 11:22 AMOpenai推出了由GPT-40提供动力的新图像生成器后,病毒热潮迅速吸引,立即吸引了许多渴望实验的用户。创建自己或其他任何人的玩具版本(包括宠物,是的),类似地工作:uplo
 6个CHATGPT提示获得增强品牌的播客邀请函Apr 16, 2025 am 11:16 AM
6个CHATGPT提示获得增强品牌的播客邀请函Apr 16, 2025 am 11:16 AM许多企业主围坐在等待永远不会到达的邀请,因为获得播客面试需要策略和持续的行动。今天采取行动。 这些提示将使您成为完美的客人,并降落这些职业
 5强大的AI提示可以提高任何业务想法Apr 16, 2025 am 11:11 AM
5强大的AI提示可以提高任何业务想法Apr 16, 2025 am 11:11 AM幸运的是,这是一个生成AI的领域,可以非常有帮助。不,它不会带来万无一失的策略。但这可以帮助您集思广益,研究市场以及微调营销内容和消息传递。 不是
 Smart研究生:AI时代的职业建议Apr 16, 2025 am 11:10 AM
Smart研究生:AI时代的职业建议Apr 16, 2025 am 11:10 AM只有今年只有不同。不确定。 关税战争正在进行中,这不仅仅是事实。 AI是最近抓挠和灵魂搜索的根本原因。国家青年慈善机构最近对
 有效的加速主义或亲社会AI。 AI的未来是什么?Apr 16, 2025 am 11:09 AM
有效的加速主义或亲社会AI。 AI的未来是什么?Apr 16, 2025 am 11:09 AM加速主义者的愿景:全速前进 有效的加速主义,即短期内被称为E/ACC,在2022年左右出现,是一种技术优越的运动,在硅谷及其他地区获得了巨大的牵引
 Excel中的相对,绝对和混合参考是什么?Apr 16, 2025 am 11:03 AM
Excel中的相对,绝对和混合参考是什么?Apr 16, 2025 am 11:03 AM介绍 我最初的电子表格经历令人沮丧,因为复制时公式的行为不可预测。 那时我不了解细胞引用,但是掌握亲戚,绝对和混合的参考文献彻底改变了我的广播。
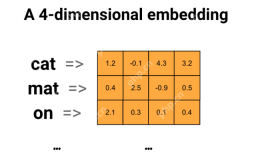 Word2Vec的智能主题电子邮件线生成Apr 16, 2025 am 11:01 AM
Word2Vec的智能主题电子邮件线生成Apr 16, 2025 am 11:01 AM本文演示了如何使用Word2Vec嵌入生成有效的电子邮件主题行。 它可以指导您建立一个利用语义相似性来创建上下文相关主题行,改善电子邮件营销的系统
 数据分析师的未来Apr 16, 2025 am 11:00 AM
数据分析师的未来Apr 16, 2025 am 11:00 AM数据分析:导航不断发展的景观 想象一个世界,数据不仅是数字,而且是每个管理决定的基石。 在这个动态的环境中,数据分析师是必不可少的,将原始数据转换为可操作的


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

适用于 Eclipse 的 SAP NetWeaver 服务器适配器
将Eclipse与SAP NetWeaver应用服务器集成。

Dreamweaver CS6
视觉化网页开发工具

禅工作室 13.0.1
功能强大的PHP集成开发环境

EditPlus 中文破解版
体积小,语法高亮,不支持代码提示功能

MinGW - 适用于 Windows 的极简 GNU
这个项目正在迁移到osdn.net/projects/mingw的过程中,你可以继续在那里关注我们。MinGW:GNU编译器集合(GCC)的本地Windows移植版本,可自由分发的导入库和用于构建本地Windows应用程序的头文件;包括对MSVC运行时的扩展,以支持C99功能。MinGW的所有软件都可以在64位Windows平台上运行。






