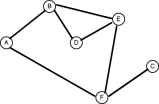
PHP主| PHP DEV的数据结构：图形-php教程-PHP中文网

首页

后端开发

php教程

PHP主| PHP DEV的数据结构：图形

Joseph Gordon-Levitt

Feb 23, 2025 am 08:49 AM

PHP主| PHP DEV的数据结构：图形

钥匙要点

图理论的常见应用是在任意两个节点之间找到最少数量的啤酒花（即最短路径）。这可以使用广度优先的搜索来实现，这涉及从指定的根节点从级别穿越图形级别。此过程需要保持未访问的节点的队列。> Dijkstra的算法被广泛用于查找图中任何两个节点之间的最短或最佳路径。这涉及检查从源节点开始的所有可能对顶点之间的每个边缘，并保持最短的总距离的更新的顶点，直到达到目标节点为止。

在我以前的一篇文章中，我向您介绍了树数据结构。现在，我想探索一个相关的结构 - 图。图具有许多现实世界应用程序，例如网络优化，流量路由和社交网络分析。 Google的Pagerank，Facebook的Graph Search以及Amazon和Netflix的建议是图形驱动应用程序的一些示例。在本文中，我将探讨使用图形的两个常见问题 - 啤酒花数量最少和最短路径问题。图是一种数学结构，用于建模键/值对之间的关系。图包含一组>顶点（节点）和连接它们的任意数量的 edges（线）。这些边缘可以指向或无向。导向边缘只是两个顶点之间的边缘，而边缘A→B不与B→A相同。无方向的边缘没有方向或方向；边缘A-B等于B-A。我们上次了解到的树结构可以被视为一种无向图的类型，其中每个顶点通过简单路径连接到至少一个其他顶点。图形也可以加权或未加权。加权图或网络是将重量或成本值分配给其每个边缘的一个网络。加权图通常用于确定最佳路径，最优势或两个点之间的最低“成本”路径。 GoogleMap的驱动方向是使用加权图的示例。最少的啤酒花

图理论的常见应用是在任意两个节点之间找到最少的啤酒花。与树一样，图形可以通过以下两种方式之一进行遍历：深度优先或广度优先。我们在上一篇文章中介绍了深度优先的搜索，因此让我们看一下广度优先的搜索。考虑以下图：

PHP主| PHP DEV的数据结构：图形为了简单起见，让我们假设该图是

的 - 即，任何方向的边缘是相同的。我们的任务是在任意两个节点之间找到最少的啤酒花。在广度优先的搜索中，我们从根节点（或指定为根的任何节点）开始，然后按级别沿着树的水平沿我们的方式进行工作。为了做到这一点，我们需要一个队列来维护未访问的节点的列表，以便我们可以在每个级别后回溯和处理它们。一般算法看起来像这样：但是，我们怎么知道哪些节点相邻，更不用说未访问的而不首先遍历图形呢？这使我们解决了如何建模图数据结构的问题。

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

代表图形

通常有两种表示图形的方法：作为邻接矩阵或邻接列表。上面的图表示为邻接列表，如下所示：

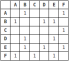
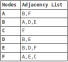PHP主| PHP DEV的数据结构：图形该图表示为矩阵，其中1表示2个顶点之间的边缘的“发生率”：

PHP主| PHP DEV的数据结构：图形

邻接列表更具空间效率，尤其是对于大多数顶点没有连接的稀疏图，而邻接矩阵有助于更快的查找。最终，表示形式的选择将取决于可能需要哪种类型的图形操作。让我们使用邻接列表来表示图表：

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

现在，让我们看看一般广度优先搜索算法的实现是什么样的：

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

运行以下示例，我们得到：

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

如果我们使用堆栈而不是队列，则遍历将成为深度优先的搜索。

找到最短路径

另一个常见的问题是找到任何两个节点之间的最佳路径。早些时候，我提到了GoogleMap的行驶方向，以此为例。其他应用程序包括规划旅行行程，道路交通管理以及火车/公共汽车计划。解决此问题的最著名算法之一是由一位29岁的计算机科学家以Edsger W. Dijkstra的名义发明的。总的来说，Dijkstra的解决方案涉及检查从源节点开始的所有可能的顶点之间的每个边缘，并保持最短的总距离的更新的顶点，直到达到目标节点，或者无法达到目标节点，任何情况下的情况下。有几种方法可以实施该解决方案，实际上，在1959年，使用Minheaps，Priorityqueues和Fibonacci堆的多年以来，都对Dijkstra的原始算法做出了。一些改进的性能，而另一些则旨在解决Dijkstra解决方案中的缺点，因为它仅适用于正加权图（权重为正值）。这是一个（正）加权图的示例：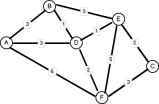

PHP主| PHP DEV的数据结构：图形

我们可以将此图表示为邻接列表，如下所示：

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

这是使用PriorityQueue来维护所有“不优化”顶点的列表的实现：

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

如您所见，Dijkstra的解决方案只是广度优先搜索的变体！运行以下示例会产生以下结果：

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

摘要

在本文中，我介绍了图理论的基础知识，两种表示图形的方法以及图理论应用中的两个基本问题。我向您展示了如何使用广度优先的搜索来找到任何两个节点之间最少的啤酒花，以及如何使用Dijkstra的解决方案来找到任何两个节点之间的最短路径。通过fotolia 图像经常询问数据结构中图的问题（常见问题解答）

数据结构中的图和树之间有什么区别？树是一种类型，但并非所有图形都是树。树是没有任何周期的连接图。它具有带根节点和子节点的层次结构。树上的每个节点都有一个独特的路径。另一方面，图可以具有循环，其结构更为复杂。它可以连接或断开连接，节点之间可以具有多个路径。列表。邻接矩阵是大小为v x v的2D数组，其中v是图中的顶点数。如果顶点I和J之间有边缘，则第I和J列的交点处的单元格为1，否则为0。邻接列表是链接列表的数组。数组的索引代表一个顶点，其链接列表中的每个元素代表与顶点形成边缘的其他顶点。是数据结构中几种类型的图形。一个简单的图是一个没有循环的图形，在任何两个顶点之间不超过一个边缘。多编码可以在顶点之间具有多个边缘。完整的图是一个简单的图形，其中每对顶点都通过边缘连接。加权图为每个边缘分配一个权重。有向图（或Digraph）具有方向的边缘。边缘从一个顶点到另一个顶点。

在计算机科学中的许多应用中，都使用了图表中图中图的应用？它们在社交网络中用于表示人们之间的联系。它们用于网络爬行中访问网页并构建搜索索引。它们用于网络路由算法中，以找到两个节点之间的最佳路径。它们在生物学中用于建模和分析生物网络。它们也用于计算机图形和物理模拟中。

>图形遍历算法是什么？

>有两个主要的图形遍历算法：Depth-First Search（DFS）和广度优先搜索（BFS）。 DFS在回溯之前尽可能沿每个分支探索。它使用堆栈数据结构。 BFS探索当前深度的所有顶点，然后才能进入下一个级别。它使用队列数据结构。

如何在Java中实现图形？ hashmap中的每个键都是顶点，其值是一个链接列表，包含其连接到的顶点。

>什么是两部分图？

二键图是一个图形，是一个图形的图形。被分为两个不相交的集合，使每个边缘在一个集合中连接一个顶点与另一组顶点连接。没有边界在同一集合中连接顶点。

什么是子图？

一个子图是一个图形，是另一个图的一部分。它具有原始图的某些（或全部）顶点，以及原始图的某些（或全）边缘。

>图中的一个周期是什么？一条从同一顶点开始和结束的路径，至少具有一个边。的连续的顶点通过边缘连接。

以上是PHP主| PHP DEV的数据结构：图形的详细内容。更多信息请关注PHP中文网其他相关文章！

声明

本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系admin@php.cn

可以在PHP会话中存储哪些数据？May 02, 2025 am 12:17 AM

phpsessionscanStorestrings，数字，数组和原始物。

您如何开始PHP会话？May 02, 2025 am 12:16 AM

tostartaphpsession，usesesses_start（）attheScript'Sbeginning.1）placeitbeforeanyOutputtosetThesessionCookie.2）useSessionsforuserDatalikeloginstatusorshoppingcarts.3）regenerateSessiveIdStopreventFentfixationAttacks.s.4）考虑使用AttActAcks.s.s.4）

什么是会话再生，如何提高安全性？May 02, 2025 am 12:15 AM

会话再生是指在用户进行敏感操作时生成新会话ID并使旧ID失效，以防会话固定攻击。实现步骤包括：1.检测敏感操作，2.生成新会话ID，3.销毁旧会话ID，4.更新用户端会话信息。

使用PHP会话时有哪些性能考虑？May 02, 2025 am 12:11 AM

PHP会话对应用性能有显着影响。优化方法包括：1.使用数据库存储会话数据，提升响应速度；2.减少会话数据使用，只存储必要信息；3.采用非阻塞会话处理器，提高并发能力；4.调整会话过期时间，平衡用户体验和服务器负担；5.使用持久会话，减少数据读写次数。

PHP会话与Cookie有何不同？May 02, 2025 am 12:03 AM

PHPsessionsareserver-side,whilecookiesareclient-side.1)Sessionsstoredataontheserver,aremoresecure,andhandlelargerdata.2)Cookiesstoredataontheclient,arelesssecure,andlimitedinsize.Usesessionsforsensitivedataandcookiesfornon-sensitive,client-sidedata.

PHP如何识别用户的会话？May 01, 2025 am 12:23 AM

phpientifiesauser'ssessionusessessionSessionCookiesAndSessionIds.1）whiwSession_start（）被称为，phpgeneratesainiquesesesessionIdStoredInacookInAcookInamedInAcienamedphpsessidontheuser'sbrowser'sbrowser.2）thisIdAllowSphptptpptpptpptpptortoreTessessionDataAfromtheserverMtheserver。

确保PHP会议的一些最佳实践是什么？May 01, 2025 am 12:22 AM

PHP会话的安全可以通过以下措施实现：1.使用session_regenerate_id()在用户登录或重要操作时重新生成会话ID。2.通过HTTPS协议加密传输会话ID。3.使用session_save_path()指定安全目录存储会话数据，并正确设置权限。

PHP会话文件默认存储在哪里？May 01, 2025 am 12:15 AM

phpsessionFilesArestoredIntheDirectorySpecifiedBysession.save_path，通常是/tmponunix-likesystemsorc：\ windows \ windows \ temponwindows.tocustomizethis：tocustomizEthis：1）useession_save_save_save_path_path（）

See all articles