JavaScript is frequently ridiculed when developers first encounter this seemingly baffling result:
0.1 + 0.2 == 0.30000000000000004
Memes about JavaScript's handling of numbers are widespread, often leading many to believe that this behaviour is unique to the language.
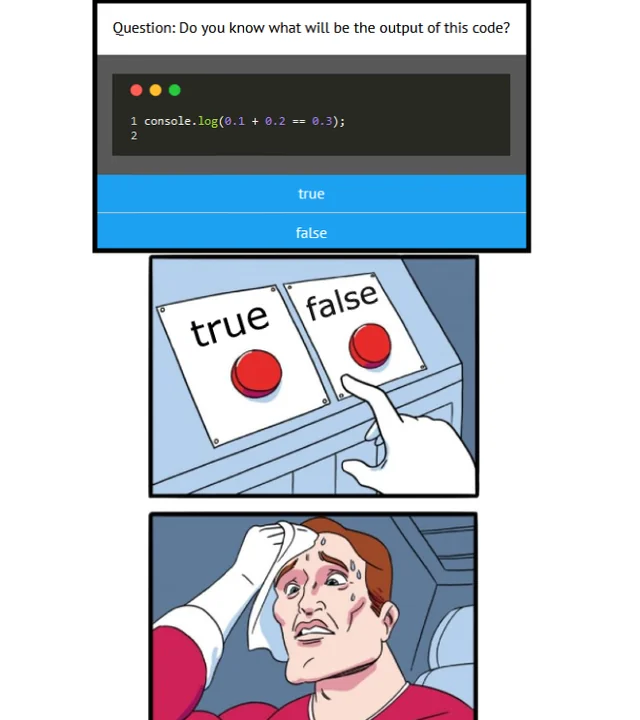
However, this quirk isn't just limited to JavaScript. It is a consequence of how most programming languages handle floating-point arithmetic.
For instance, here are code snippets from Java and Go that produce similar results:

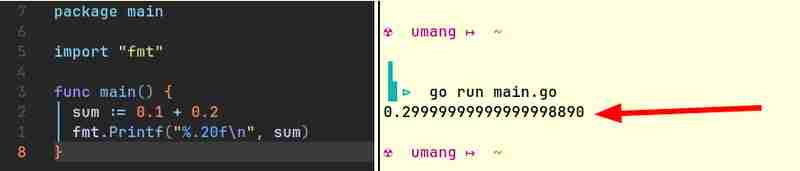
Computers can natively only store integers. They don't understand fractions. (How will they? The only way computers can do arithmetic is by turning some lights on or off. The light can either be on or off. It can't be "half" on!) They need some way of representing floating point numbers. Since this representation is not perfectly accurate, more often than not, 0.1 + 0.2 does not equal 0.3.
All fractions whose denominators are made of prime factors of the number system's base can be cleanly expressed while any other fractions would have repeating decimals. For example, in the number system with base 10, fractions like 1/2, 1/4, 1/5, 1/10 are cleanly represented because the denominators in each case are made up of 2 or 5 - the prime factors of 10. However, fractions like 1/3, 1/6, 1/7 all have recurring decimals.
Similarly, in the binary system fractions like 1/2, 1/4, 1/8 are cleanly expressed while all other fractions have recurring decimals. When you perform arithmetic on these recurring decimals, you end up with leftovers which carry over when you convert the computer's binary representation of numbers to a human readable base-10 representation. This is what leads to approximately correct results.
Now that we've established that this problem is not exclusive to JavaScript, let's explore how floating-point numbers are represented and processed under the hood to understand why this behaviour occurs.
In order to understand how floating point numbers are represented and processed under the hood, we would first have to understand the IEEE 754 floating point standard.
IEEE 754 standard is a widely used specification for representing and performing arithmetic on floating-point numbers in computer systems. It was created to guarantee consistency when using floating-point arithmetic on various computing platforms. Most programming languages and hardware implementations (CPUs, GPUs, etc.) adhere to this standard.
This is how a number is denoted in IEEE 754 format:
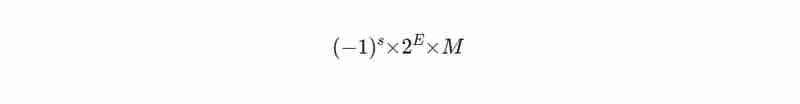
Here s is the sign bit (0 for positive, 1 for negative), M is the mantissa (holds the digits of the number) and E is the exponent which determines the scale of the number.
You would not be able to find any integer values for M and E that can exactly represent numbers like 0.1, 0.2 or 0.3 in this format. We can only pick values for M and E that give the closest result.
Here is a tool you could use to determine the IEEE 754 notations of decimal numbers: https://www.h-schmidt.net/FloatConverter/IEEE754.html
IEEE 754 notation of 0.25:
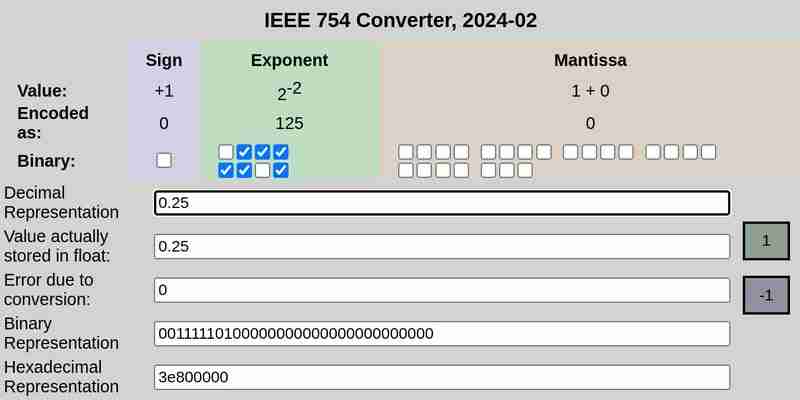
IEEE 754 notation of 0.1 and 0.2 respectively:
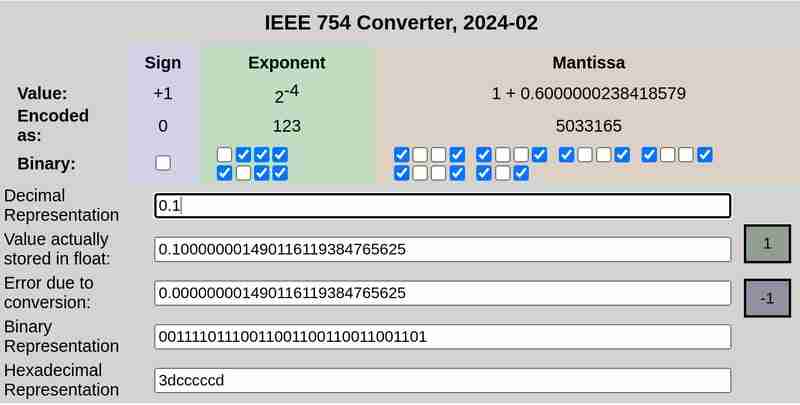

Please note that the error due to conversion in case of 0.25 was 0, while 0.1 and 0.2 had non-zero errors.
IEEE 754 defines the following formats for representing floating-point numbers:
Single-precision (32-bit): 1 bit for sign, 8 bits for exponent, 23 bits for mantissa
Double-precision (64-bit): 1 bit for sign, 11 bits for exponent, 52 bits for mantissa
For the sake of simplicity, let us consider the single-precision format that uses 32 bits.
The 32 bit representation of 0.1 is:
0 01111011 10011001100110011001101
Here the first bit represents the sign (0 which means positive in this case), the next 8 bits (01111011) represent the exponent and the final 23 bits (10011001100110011001101) represent the mantissa.
This is not an exact representation. It represents ≈ 0.100000001490116119384765625
Similarly, the 32 bit representation of 0.2 is:
0 01111100 10011001100110011001101
This is not an exact representation either. It represents ≈ 0.20000000298023223876953125
When added, this results in:
0 01111101 11001101010011001100110
which is ≈ 0.30000001192092896 in decimal representation.
In conclusion, the seemingly perplexing result of 0.1 + 0.2 not yielding 0.3 is not an anomaly specific to JavaScript, but a consequence of the limitations of floating-point arithmetic across programming languages. The roots of this behaviour lie in the binary representation of numbers, which inherently leads to precision errors when handling certain fractions.
以上是Beyond JavaScript - Why + doesn&#t equal in programming的详细内容。更多信息请关注PHP中文网其他相关文章!
 Python vs. JavaScript:开发人员的比较分析May 09, 2025 am 12:22 AM
Python vs. JavaScript:开发人员的比较分析May 09, 2025 am 12:22 AMPython和JavaScript的主要区别在于类型系统和应用场景。1.Python使用动态类型,适合科学计算和数据分析。2.JavaScript采用弱类型,广泛用于前端和全栈开发。两者在异步编程和性能优化上各有优势,选择时应根据项目需求决定。
 Python vs. JavaScript:选择合适的工具May 08, 2025 am 12:10 AM
Python vs. JavaScript:选择合适的工具May 08, 2025 am 12:10 AM选择Python还是JavaScript取决于项目类型:1)数据科学和自动化任务选择Python;2)前端和全栈开发选择JavaScript。Python因其在数据处理和自动化方面的强大库而备受青睐,而JavaScript则因其在网页交互和全栈开发中的优势而不可或缺。
 Python和JavaScript:了解每个的优势May 06, 2025 am 12:15 AM
Python和JavaScript:了解每个的优势May 06, 2025 am 12:15 AMPython和JavaScript各有优势,选择取决于项目需求和个人偏好。1.Python易学,语法简洁,适用于数据科学和后端开发,但执行速度较慢。2.JavaScript在前端开发中无处不在,异步编程能力强,Node.js使其适用于全栈开发,但语法可能复杂且易出错。
 JavaScript的核心:它是在C还是C上构建的?May 05, 2025 am 12:07 AM
JavaScript的核心:它是在C还是C上构建的?May 05, 2025 am 12:07 AMjavascriptisnotbuiltoncorc; saninterpretedlanguagethatrunsonenginesoftenwritteninc.1)javascriptwasdesignedAsalightweight,解释edganguageforwebbrowsers.2)Enginesevolvedfromsimpleterterterpretpreterterterpretertestojitcompilerers,典型地提示。
 JavaScript应用程序:从前端到后端May 04, 2025 am 12:12 AM
JavaScript应用程序:从前端到后端May 04, 2025 am 12:12 AMJavaScript可用于前端和后端开发。前端通过DOM操作增强用户体验,后端通过Node.js处理服务器任务。1.前端示例:改变网页文本内容。2.后端示例:创建Node.js服务器。
 Python vs. JavaScript:您应该学到哪种语言?May 03, 2025 am 12:10 AM
Python vs. JavaScript:您应该学到哪种语言?May 03, 2025 am 12:10 AM选择Python还是JavaScript应基于职业发展、学习曲线和生态系统:1)职业发展:Python适合数据科学和后端开发,JavaScript适合前端和全栈开发。2)学习曲线:Python语法简洁,适合初学者;JavaScript语法灵活。3)生态系统:Python有丰富的科学计算库,JavaScript有强大的前端框架。
 JavaScript框架:为现代网络开发提供动力May 02, 2025 am 12:04 AM
JavaScript框架:为现代网络开发提供动力May 02, 2025 am 12:04 AMJavaScript框架的强大之处在于简化开发、提升用户体验和应用性能。选择框架时应考虑:1.项目规模和复杂度,2.团队经验,3.生态系统和社区支持。
 JavaScript,C和浏览器之间的关系May 01, 2025 am 12:06 AM
JavaScript,C和浏览器之间的关系May 01, 2025 am 12:06 AM引言我知道你可能会觉得奇怪,JavaScript、C 和浏览器之间到底有什么关系?它们之间看似毫无关联,但实际上,它们在现代网络开发中扮演着非常重要的角色。今天我们就来深入探讨一下这三者之间的紧密联系。通过这篇文章,你将了解到JavaScript如何在浏览器中运行,C 在浏览器引擎中的作用,以及它们如何共同推动网页的渲染和交互。JavaScript与浏览器的关系我们都知道,JavaScript是前端开发的核心语言,它直接在浏览器中运行,让网页变得生动有趣。你是否曾经想过,为什么JavaScr


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

SublimeText3 英文版
推荐:为Win版本,支持代码提示!

SublimeText3 Linux新版
SublimeText3 Linux最新版

适用于 Eclipse 的 SAP NetWeaver 服务器适配器
将Eclipse与SAP NetWeaver应用服务器集成。

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

安全考试浏览器
Safe Exam Browser是一个安全的浏览器环境,用于安全地进行在线考试。该软件将任何计算机变成一个安全的工作站。它控制对任何实用工具的访问,并防止学生使用未经授权的资源。





