数据结构和算法：图

介绍

图是一种数据结构，具有多个顶点（节点）和它们之间的边（连接）。

树是图的一个例子。每棵树都是一个图，但并非每个图都是树，例如，有环的图就不是树。一棵树将有一个根和两个节点之间的一条唯一路径，而图可以有多个根和顶点之间的多个路径。

基本术语

顶点: 图中的节点。

边: 两个顶点之间的连接。

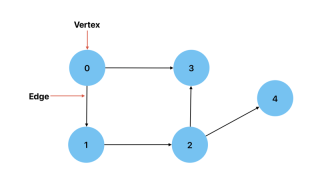
有向: 当两个顶点之间的连接有方向时。这意味着只有一种方法可以从一个顶点到达另一个顶点。一个例子是显示城市（顶点）和它们之间的路线（边）的图表。

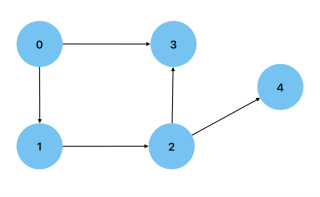
无向: 当图上两个顶点之间的连接是双向的时。一个例子是显示通过友谊连接的人（顶点）的图表。

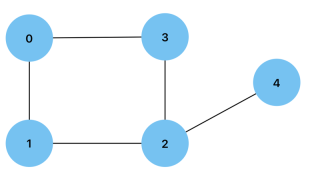
度数: 连接到顶点的边数。有向图的顶点可以具有入度或出度，分别是指向和远离顶点的边的数量。

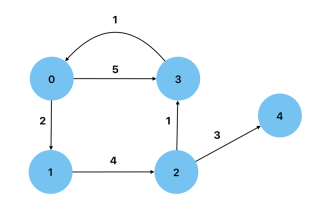
加权: 边的值作为权重的图。一个例子是路线图，其中节点之间的距离表示为权重。

循环： 具有从至少一个顶点返回自身的路径的图。

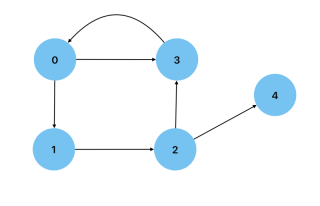
非循环: 没有循环的图，也就是说，没有节点有返回自身的路径。 有向无环图是一种可用于显示数据处理流程的图。

密集:当图的边数接近最大可能数时

稀疏: 当图的边数接近最小可能数量时。

自循环: 当一条边有一个顶点链接到其自身时。

多边: 当图在两个顶点之间具有多条边时。

简单:当图没有自环或多边时。

获取简单有向图中的最大边数：n*(n-1)，其中 n 是节点数。

要获取简单无向图中的最大边数：n*(n-1)/2，其中 n 是节点数。

在 JavaScript 中实现图表

要实现图，我们可以从指定图的顶点和边开始，下面是如何在给定图的情况下执行此操作的示例：

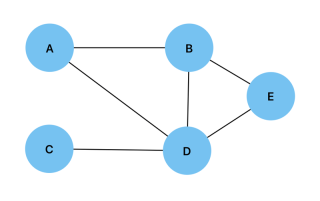
const vertices = ["A", "B", "C", "D", "E"];

const edges = [
  ["A", "B"],
  ["A", "D"],
  ["B", "D"],
  ["B", "E"],
  ["C", "D"],
  ["D", "E"],
];

然后我们可以创建一个函数来查找与给定顶点相邻的内容：

const findAdjacentNodes = function (node) {
  const adjacentNodes = [];
  for (let edge of edges) {
    const nodeIndex = edge.indexOf(node);
    if (nodeIndex > -1) {
      let adjacentNode = nodeIndex === 0 ? edge[1] : edge[0];
      adjacentNodes.push(adjacentNode);
    }
  }
  return adjacentNodes;
};

还有另一个检查两个顶点是否连接的函数：

const isConnected = function (node1, node2) {
  const adjacentNodes = new Set(findAdjacentNodes(node1));
  return adjacentNodes.has(node2);
};

邻接表

邻接列表是图的表示形式，其中连接到节点的所有顶点都存储为列表。下面是一个图表及其相应邻接列表的直观表示。

邻接列表可以通过创建两个类（Node 类和 Graph 类）在 JavaScript 中实现。 Node 类将包含一个构造函数和一个连接两个顶点的 connect() 方法。它还具有 isConnected() 和 getAdjacentNodes() 方法，其工作方式与上面所示的完全相同。

class Node {
  constructor(value) {
    this.value = value;
    this.edgesList = [];
  }
  connect(node) {
    this.edgesList.push(node);
    node.edgesList.push(this);
  }
  getAdjNodes() {
    return this.edgesList.map((edge) => edge.value);
  }
  isConnected(node) {
    return this.edgesList.map((edge) => 
    edge.value).indexOf(node.value) > -1;
  }
}

Graph 类由构造函数和 addToGraph() 方法组成，该方法向图中添加新顶点。

class Graph {
  constructor(nodes) {
    this.nodes = [...nodes];
  }
  addToGraph(node) {
    this.nodes.push(node);
  }
}

Adjacency Matrix

A 2-D array where each array represents a vertex and each index represents a possible connection between vertices. An adjacency matrix is filled with 0s and 1s, with 1 representing a connection. The value at adjacencyMatrix[node1][node2] will show whether or not there is a connection between the two specified vertices. Below is is a graph and its visual representation as an adjacency matrix.

To implement this adjacency matrix in JavaScript, we start by creating two classes, the first being the Node class:

class Node {
  constructor(value) {
    this.value = value;
  }
}

We then create the Graph class which will contain the constructor for creating the 2-D array initialized with zeros.

class Graph {
  constructor(nodes) {
    this.nodes = [...nodes];
    this.adjacencyMatrix = Array.from({ length: nodes.length },   
    () => Array(nodes.length).fill(0));
   }
}

We will then add the addNode() method which will be used to add new vertices to the graph.

  addNode(node) {
    this.nodes.push(node);
    this.adjacencyMatrix.forEach((row) => row.push(0));
    this.adjacencyMatrix.push(new Array(this.nodes.length).fill(0));
  }

Next is the connect() method which will add an edge between two vertices.

  connect(node1, node2) {
    const index1 = this.nodes.indexOf(node1);
    const index2 = this.nodes.indexOf(node2);

    if (index1 > -1 && index2 > -1) {
      this.adjacencyMatrix[index1][index2] = 1;
      this.adjacencyMatrix[index2][index1] = 1; 
    }
  }

We will also create the isConnected() method which can be used to check if two vertices are connected.

  isConnected(node1, node2) {
    const index1 = this.nodes.indexOf(node1);
    const index2 = this.nodes.indexOf(node2);

    if (index1 > -1 && index2 > -1) {
      return this.adjacencyMatrix[index1][index2] === 1;
    }
    return false;
  }

Lastly we will add the printAdjacencyMatrix() method to the Graph class.

  printAdjacencyMatrix() {
    console.log(this.adjacencyMatrix);
  }

Breadth First Search

Similar to a Breadth First Search in a tree, the vertices adjacent to the current vertex are visited before visiting any subsequent children. A queue is the data structure of choice when performing a Breadth First Search on a graph.

Below is a graph of international airports and their connections and we will use a Breadth First Search to find the shortest route(path) between two airports(vertices).

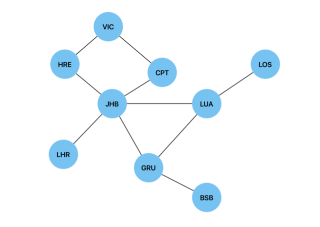
In order to implement this search algorithm in JavaScript, we will use the same Node and Graph classes we implemented the adjacency list above. We will create a breadthFirstTraversal() method and add it to the Graph class in order to traverse between two given vertices. This method will have the visitedNodes object, which will be used to store the visited vertices and their predecessors. It is initiated as null to show that the first vertex in our search has no predecessors.

breathFirstTraversal(start, end) {
    const queue = [start];
    const visitedNodes = {};
    visitedNodes[start.value] = null;

    while (queue.length > 0) {
      const node = queue.shift();

      if (node.value === end.value) {
        return this.reconstructedPath(visitedNodes, end);
      }
      for (const adjacency of node.edgesList) {
        if (!visitedNodes.hasOwnProperty(adjacency.value)) {
          visitedNodes[adjacency.value] = node;
          queue.push(adjacency);
        }
      }
    }
  }

Once the end vertex is found, we will use the reconstructedPath() method in the Graph class in order to return the shortest path between two vertices. Each vertex is added iteratively to the shortestPath array, which in turn must be reversed in order to come up with the correct order for the shortest path.

reconstructedPath(visitedNodes, endNode) {
    let currNode = endNode;

    const shortestPath = [];

    while (currNode !== null) {
      shortestPath.push(currNode.value);
      currNode = visitedNodes[currNode.value];
    }
    return shortestPath.reverse();
  }

In the case of the graph of international airports, breathFirstTraversal(JHB, LOS) will return JHB -> LUA -> LOS as the shortest path. In the case of a weighted graph, we would use Dijkstra's algorithm to find the shortest path.

Depth First Search

Similar to a depth first search in a tree, this algorithm will fully explore every descendant of a vertex, before backtracking to the root. A stack is the data structure of choice for depth first traversals in a graph.

A depth first search can be used to detect a cycle in a graph. We will use the same graph of international airports to illustrate this in JavaScript.

Similar to the Breadth First Search algorithm above, this implementation of a Depth First Search algorithm in JavaScript will use the previously created Node and Graph classes. We will create a helper function called depthFirstTraversal() and add it to the Graph class.

  depthFirstTraversal(start, visitedNodes = {}, parent = null) {
    visitedNodes[start.value] = true;

    for (const adjacency of start.edgesList) {
      if (!visitedNodes[adjacency.value]) {
        if (this.depthFirstTraversal(adjacency, visitedNodes, start)) {
          return true;
        }
      } else if (adjacency !== parent) {
        return true;
      }
    }

    return false;
  }

This will perform the Depth First Traversal of the graph, using the parent parameter to keep track of the previous vertex and prevent the detection of a cycle when revisiting the parent vertex. Visited vertices will be marked as true in the visitedNodes object. This method will then use recursion to visit previously unvisited vertices. If the vertex has already been visited, we check it against the parent parameter. A cycle has been found if the vertex has already been visited and it is not the parent.

We will also create the wrapper function hasCycle() in the Graph class. This function is used to detect a cycle in a disconnected graph. It will initialize the visitedNodes object and loop through all of the vertices in the graph.

hasCycle() {
    const visitedNodes = {};

    for (const node of this.nodes) {
      if (!visitedNodes[node.value]) {
        if (this.depthFirstTraversal(node, visitedNodes)) {
          return true;
        }
      }
    }
    return false;
  }

In the case of the graph of international airports, the code will return true.

Depth First Traversal of a graph is also useful for pathfinding(not necessarily shortest path) and for solving mazes.

结论

在进一步学习数据结构和算法时，对图作为一种数据结构及其相关算法的深刻理解是绝对必要的。尽管不像本系列之前的文章那样适合初学者，但本指南对于加深您对数据结构和算法的理解应该很有用。

以上是数据结构和算法：图的详细内容。更多信息请关注PHP中文网其他相关文章！