广度优先搜索 (BFS)

图的广度优先搜索会逐层访问顶点。第一层由起始顶点组成。每个下一个级别都由与前一个级别中的顶点相邻的顶点组成。图的广度优先遍历类似于树遍历中讨论的树的广度优先遍历。通过广度优先遍历树，逐级访问节点。首先访问根，然后访问根的所有子代，然后访问根的孙子，依此类推。类似地，图的广度优先搜索首先访问一个顶点，然后访问它的所有相邻顶点，然后访问与这些顶点相邻的所有顶点，依此类推。为了确保每个顶点仅被访问一次，如果已经访问过该顶点，则会跳过该顶点。

广度优先搜索算法

从图中的顶点 v 开始广度优先搜索的算法在下面的代码中描述。

输入：G = (V, E) 和起始顶点 v
输出：一棵以 v
为根的 BFS 树 1 树 bfs(顶点 v) {
2 创建一个空队列，用于存储要访问的顶点；
3 将v添加到队列中；
4 马克 v 访问过；
5
6 while (队列不为空) {
7 将一个顶点（例如 u）从队列中出列；
8 将u添加到遍历顶点列表中；
u 的每个邻居 w
为 9 10 如果 w 尚未被访问过 {
11 将w添加到队列中；
12 将 u 设置为树中 w 的父级；
13 马克访问过；
14 }
15 }
16 }

考虑下图 (a) 中的图表。假设从顶点 0 开始广度优先搜索。首先访问 0，然后访问其所有邻居 1、2 和 3，如下图 (b) 所示。顶点 1 有三个邻居：0、2 和 4。由于 0 和 2 已经被访问过，所以您现在将只访问 4，如下图 (c) 所示。顶点 2 有 3 个邻居：0、1 和 3，它们都已被访问过。顶点 3 有 3 个邻居：0、2 和 4，它们都已被访问过。顶点 4 有两个邻居：1 和 3，它们都已被访问过。至此，搜索结束。

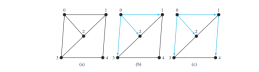
由于每条边和每个顶点仅被访问一次，因此 bfs 方法的时间复杂度为 O(|E| + |V|)，其中 | E| 表示边数，|V| 表示顶点数。

广度优先搜索的实现

bfs(int v) 方法在 Graph 接口中定义，并在 AbstractGraph.java 类中实现（第 197-222 行）。它返回以顶点 v 作为根的 Tree 类的实例。该方法将搜索到的顶点存储在列表searchOrder（第198行）中，每个顶点的父级存储在数组parent（第199行）中，使用链表作为队列（第198行） 203–204），并使用 isVisited 数组来指示顶点是否已被访问（第 207 行）。搜索从顶点 v 开始。 v 被添加到第 206 行的队列中，并被标记为已访问（第 207 行）。该方法现在检查队列中的每个顶点 u（第 210 行）并将其添加到 searchOrder（第 211 行）。该方法将 u 的每个未访问邻居 e.v 添加到队列（第 214 行），将其父级设置为 u （第 215 行），并将其标记为已访问（第 216 行）。

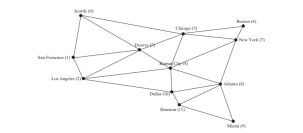
下面的代码给出了一个测试程序，显示从芝加哥开始的上图中图表的 BFS。

public class TestBFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph<string> graph = new UnweightedGraph(vertices, edges);
        AbstractGraph<string>.Tree bfs = graph.bfs(graph.getIndex("Chicago"));

        java.util.List<integer> searchOrders = bfs.getSearchOrder();
        System.out.println(bfs.getNumberOfVerticesFound() + " vertices are searched in this BFS order:");
        for(int i = 0; i 



<p>按以下顺序搜索 12 个顶点：<br>
 芝加哥 西雅图 丹佛 堪萨斯城 波士顿 纽约<br>
 旧金山 洛杉矶 亚特兰大 达拉斯 迈阿密 休斯顿<br>
西雅图的父级是芝加哥<br>
旧金山的父级是西雅图<br>
洛杉矶的父级是丹佛<br>
丹佛的父级是芝加哥<br>
堪萨斯城的母校是芝加哥<br>
波士顿的父母是芝加哥<br>
纽约的父母是芝加哥<br>
亚特兰大的母公司是堪萨斯城<br>
迈阿密的父母是亚特兰大<br>
达拉斯的父母是堪萨斯城<br>
休斯顿的父母是亚特兰大</p>

<h2>
  
  
  BFS 的应用
</h2>

<p>DFS 解决的许多问题也可以使用 BFS 解决。具体来说，BFS可以用来解决以下问题：</p>
<ul>
<li>检测图是否连通。如果图中任意两个顶点之间存在路径，则该图是连通的。</li>
<li>检测两个顶点之间是否存在路径。</li>
<li>寻找两个顶点之间的最短路径。可以证明BFS树中根到任意节点的路径都是根到节点的最短路径。</li>
<li>查找所有连接的组件。连通分量是最大连通子图，其中每对顶点都通过路径连接。</li>
<li>检测图中是否存在环路。</li>
<li>在图中找到一个循环。</li>
<li>测试图是否是二分图。 （如果图的顶点可以分为两个不相交的集合，并且同一集合中的顶点之间不存在边，则该图是二分图。）</li>
</ul>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172324339470608.png?x-oss-process=image/resize,p_40" class="lazy" alt="Breadth-First Search (BFS)"></p>


          

            
        </integer></string></string>

以上是广度优先搜索 (BFS)的详细内容。更多信息请关注PHP中文网其他相关文章！