测试 AVLTree 类

本节给出了使用 AVLTree 类的示例。下面的代码给出了一个测试程序。该程序创建一个用整数数组 25、20 和 5 初始化的 AVLTree （第 7 行），将元素插入第 11-20 行，并删除第 24-30 行中的元素。由于 AVLTree 是 BST 的子类，并且 BST 中的元素是可迭代的，因此程序使用 foreach 循环遍历第 35-37 行中的所有元素.

package demo;

public class TestAVLTree {

    public static void main(String[] args) {
        // Create an AVL tree
        AVLTree<Integer> tree = new AVLTree<>(new Integer[]{25, 20, 5});
        System.out.print("After inserting 25, 20, 5:");
        printTree(tree);

        tree.insert(34);
        tree.insert(50);
        System.out.print("\nAfter inserting 34, 50:");
        printTree(tree);

        tree.insert(30);
        System.out.print("\nAfter inserting 30");
        printTree(tree);

        tree.insert(10);
        System.out.print("\nAfter inserting 10");
        printTree(tree);

        tree.delete(34);
        tree.delete(30);
        tree.delete(50);
        System.out.print("\nAfter removing 34, 30, 50:");
        printTree(tree);

        tree.delete(5);
        System.out.print("\nAfter removing 5:");
        printTree(tree);

        System.out.print("\nTraverse the elements in the tree: ");
        for (int e: tree) {
            System.out.print(e + " ");
        }
    }

    public static void printTree(BST tree) {
        // Traverse tree
        System.out.print("\nInorder (sorted): ");
        tree.inorder();
        System.out.print("\nPostorder: ");
        tree.postorder();
        System.out.print("\nPreorder: ");
        tree.preorder();
        System.out.print("\nThe number of nodes is " + tree.getSize());
        System.out.println();
    }
}

插入 25、20、5 后：
Inorder（已排序）：5 20 25
邮购日期：5 25 20
预购：20 5 25
节点数为3

插入 34、50 后：
Inorder（已排序）：5 20 25 34 50
邮购：5 25 50 34 20
预购：20 5 34 25 50
节点数为5

插入30后
Inorder（已排序）：5 20 25 30 34 50
邮购：5 20 30 50 34 25
预购：25 20 5 34 30 50
节点数为6

插入 10 个后
Inorder（已排序）：5 10 20 25 30 34 50
邮购：5 20 10 30 50 34 25
预购：25 10 5 20 34 30 50
节点数为 7

删除 34、30、50 后：
Inorder（已排序）：5 10 20 25
邮购：5 20 25 10
预购：10 5 25 20
节点数为4

删除 5 个后：
Inorder（已排序）：10 20 25
邮购日期：10 25 20
预购：20 10 25
节点数为3

遍历树中的元素：10 20 25

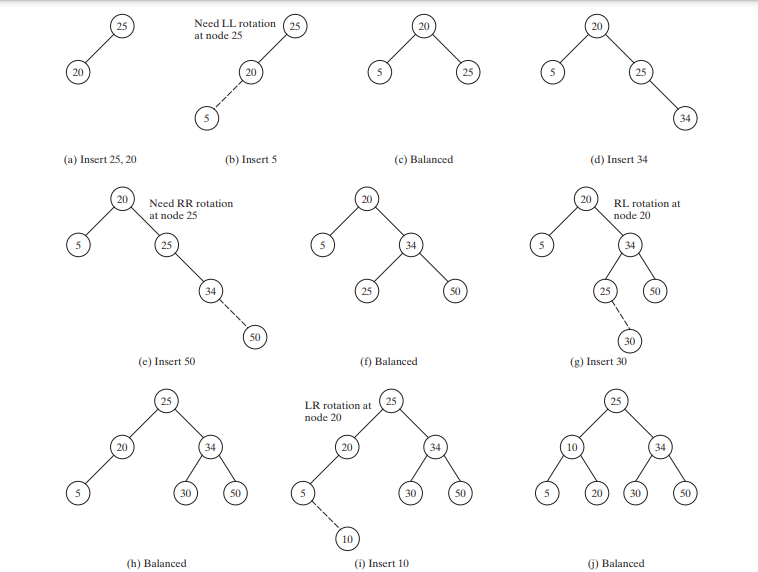
下图显示了随着元素添加到树中，树是如何演变的。添加25和20后，树如下图(a)所示。 5作为20的左孩子插入，如下图(b)所示。这棵树不平衡。它在节点 25 处为左重。执行 LL 旋转以生成 AVL 树，如下图 (c) 所示。

插入34后，树如下图(d)所示。插入50后，树如下图(e)所示。这棵树不平衡。它在节点 25 处为右重。执行 RR 旋转，得到 AVL 树，如下图 (f) 所示。

插入30后，树如下图(g)所示。这棵树不平衡。进行RL旋转得到AVL树，如下图(h)所示。

插入10后，树如下图(i)所示。这棵树不平衡。进行LR旋转得到AVL树，如下图(j)所示。

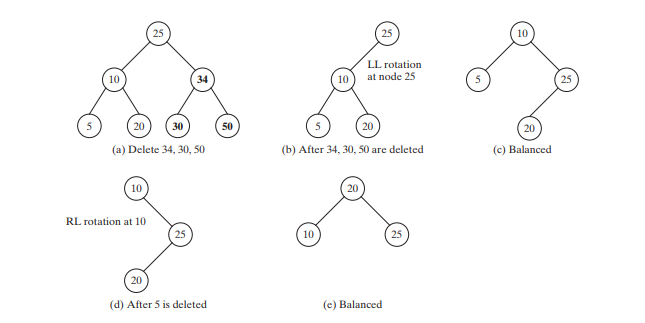
下图显示了树如何随着元素被删除而演变。删除34、30、50后，树如下图(b)所示。这棵树不平衡。进行LL旋转得到AVL树，如下图(c)所示。

删除5后，树如下图(d)所示。这棵树不平衡。进行RL旋转得到AVL树，如下图(e)

以上是测试 AVLTree 类的详细内容。更多信息请关注PHP中文网其他相关文章！