K 最近邻回归，回归：监督机器学习

k-最近邻回归

k-最近邻（k-NN）回归是一种非参数方法，它根据特征空间中 k 个最近训练数据点的平均值（或加权平均值）来预测输出值。这种方法可以有效地对数据中的复杂关系进行建模，而无需假设特定的函数形式。

k-NN回归方法可以总结如下：

1. 距离度量：该算法使用距离度量（通常为欧几里得距离）来确定数据点的“接近程度”。
2. k 个邻居：参数 k 指定在进行预测时要考虑多少个最近邻居。
3. 预测：新数据点的预测值是其 k 个最近邻的值的平均值。

关键概念

1. 非参数：与参数模型不同，k-NN 不假设输入特征和目标变量之间的潜在关系的特定形式。这使得它可以灵活地捕获复杂的模式。

2. 距离计算：距离度量的选择可以显着影响模型的性能。常见指标包括欧几里德距离、曼哈顿距离和闵可夫斯基距离。

3. k 的选择：可以基于交叉验证来选择邻居的数量 (k)。小 k 可能会导致过度拟合，而大 k 可能会过度平滑预测，从而可能导致欠拟合。

k-最近邻回归示例

此示例演示了如何使用具有多项式特征的 k-NN 回归来建模复杂关系，同时利用 k-NN 的非参数性质。

Python 代码示例

1。导入库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

此块导入数据操作、绘图和机器学习所需的库。

2。生成样本数据

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel() + np.sin(2 * X.ravel()) * 5 + np.random.normal(0, 1, 100)

该块生成表示与一些噪声的关系的样本数据，模拟现实世界的数据变化。

3。分割数据集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

此块将数据集拆分为训练集和测试集以进行模型评估。

4。创建多项式特征

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

该块从训练和测试数据集中生成多项式特征，使模型能够捕获非线性关系。

5。创建并训练 k-NN 回归模型

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

此块初始化 k-NN 回归模型并使用从训练数据集导出的多项式特征对其进行训练。

6。做出预测

y_pred = knn_model.predict(X_poly_test)

此块使用经过训练的模型对测试集进行预测。

7。绘制结果

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

此块创建实际数据点与 k-NN 回归模型的预测值的散点图，可视化拟合曲线。

k = 1 时的输出：

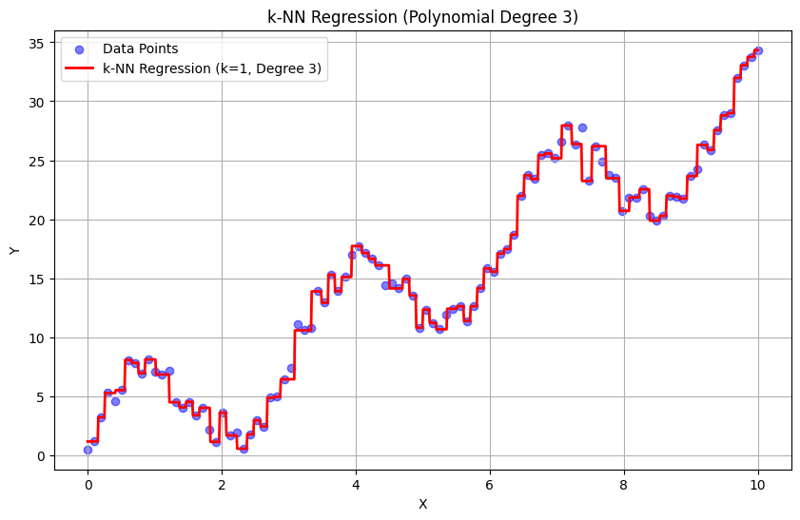
k = 10 时的输出：

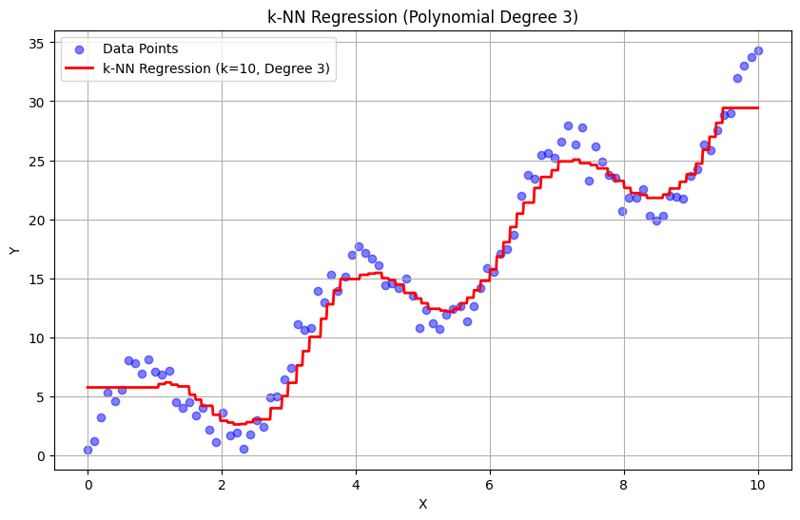
这种结构化方法演示了如何使用多项式特征实现和评估 k-最近邻回归。通过对附近邻居的响应进行平均来捕获局部模式，k-NN 回归可以有效地对数据中的复杂关系进行建模，同时提供简单的实现。 k 和多项式次数的选择会显着影响模型在捕捉潜在趋势方面的性能和灵活性。

以上是K 最近邻回归，回归：监督机器学习的详细内容。更多信息请关注PHP中文网其他相关文章！