DeepMind开发用于量子化学计算的神经网络变分蒙特卡罗
- PHPz原创
- 2024-07-16 15:26:30574浏览

近百年前,狄拉克提出正电子概念,如今在医学物理、天体物理及材料科学等多个领域都具有技术相关性。然而,正电子-分子复合物基态性质的量子化学计算具有挑战性。
在此,DeepMind 和伦敦帝国理工学院的研究人员,使用最近开发的费米子神经网络 (FermiNet) 波函数来解决这个问题,该波函数不依赖于基组。研究发现 FermiNet 可以在一系列具有各种不同定性正电子结合特性的原子和小分子中产生高度精确的、在某些情况下是最先进的基态能量。
研究人员计算了具有挑战性的非极性苯分子的结合能,发现与实验值高度一致,并得到了与使用显式相关的高斯波函数获得的湮灭率相比更有利的湮灭率。结果证明了基于神经网络波函数的方法的通用优势,并将其应用于标准分子哈密顿量以外的系统。
相关研究以《Neural network variational Monte Carlo for positronic chemistry》为题,于 6 月 18 日发布在《Nature Communications》上。

正电子-分子复合物基态性质的量子化学计算具有挑战性。主要困难在于采用适当的基组来表示电子和正电子之间的融合(coalescence)。
尽管正电子与电子接触时会湮灭,但它们很容易与普通分子形成束缚态。已经有许多计算化学标准工具对正电子结合能和湮灭率进行了理论计算。但由于多种原因,描述正电子波函数仍然具有挑战性。
在此,研究人员提出了一种计算分子正电子束缚态基态特性的新方法,该方法基于最近为 QMC 开发的神经网络波函数假设。费米子神经网络 (FermiNet) 无需参考一组基函数即可对多体波函数进行建模。这方便地避开了上述描述正电子波函数的许多困难。
研究人员扩展了 FermiNet,以与电子分量同等地表示波函数的正电子分量。只需对神经网络架构进行最小程度的改动,就可以获得灵活而准确的混合电子-正电子波函数假设。计算了一系列具有不同正电子结合机制的系统的正电子结合能和湮灭率,并获得了这些系统基态能量的最高精度。
对正电子氢化物、钠和镁原子以及小双原子分子的结果表明,与以前的研究相比,该方法可以达到最先进的精度。此外,对非极性二锂和苯分子的结果表明,在描述完全由强电子-正电子关联效应控制的正电子结合模式时,这种精度得以保留。
下图提供了对非极性分子和正电子之间结合机制的直观理解:关联主导的结合是由远离分子原子核的电子密度增加的中心促进的。在双锂中,这是共价键;在苯中,这是由于环中 π 键的离域而导致的分子中心电子密度的增加。

表:与通过其他各种计算方法获得的湮灭率相比,使用 FermiNet 波函数积累的正电子原子和分子的 2γ 湮灭率。(来源:论文)
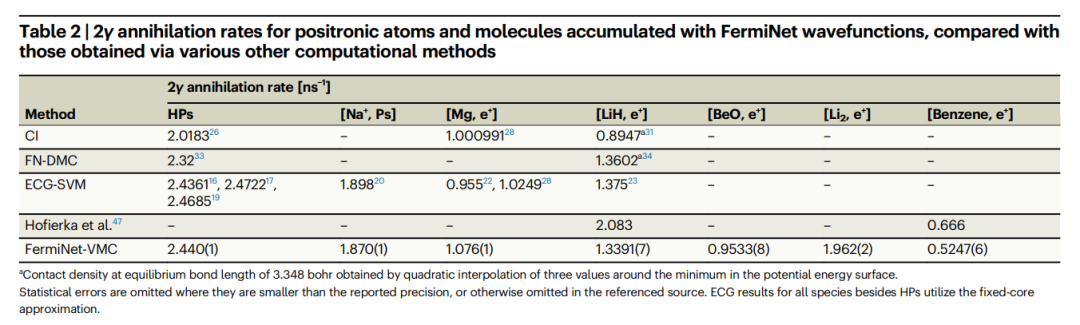
2.研究发现,对于正电子氢化物、氢化锂和碱金属原子,FermiNet-VMC 和 ECG-SVM 的湮没率结果非常一致。
- 这表明 FermiNet-VMC 提供了准确的电子-正电子相关性描述,并且比 Hofierka 等人的多体理论结果更适合计算湮没率。
- 总之,ECG-SVM 方法无需系统特定的调整,即可为具有各种正电子结合机制的多种分子产生高度准确的结果。
以上是DeepMind开发用于量子化学计算的神经网络变分蒙特卡罗的详细内容。更多信息请关注PHP中文网其他相关文章!
声明:
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系admin@php.cn

