c++ - 如何实现去除所有集合内可以组成加法运算的子集

Question

给一组数列，若数列内存在一个数等于数列内其他一些数的和，则去除那些数。此删除操作可重复操作直到无法继续找到满足条件的数进行删除。请写出一个函数，输入为整型数组，经过函数内一系列删除操作后得到一个最...

ringa_lee · Answer

這個問題目測NPC妥妥的。可以分「兩步走」。

找出所有「加法子集」。取每個元素為可能的和，利用subset sum演算法逐一求解。
尋找互斥的加法子集的最大並集：參考set packing演算法，用線性規劃求解。

以下用 Mathematica 詳細描述下演算法。

找加法子集

要列舉集合中所有構成加法式子的數字（允許數字是負數，也允許重複數字），首先借subset sum演算法（帶快取的遞歸），列舉出其和是某給定數字的子集。

subsetSum[lst_List, s_] := Block[{q},
  q[k_?NonPositive, x_] := {};
  q[k_?Positive, x_] := q[k, x] =
    Union[q[k - 1, x],
     If[lst[[k]] == x, {{x}}, {}],
     (Append[lst[[k]]] /* Sort) /@ q[k - 1, x - lst[[k]]]];
  q[Length[lst], s]]

程式碼對q進行遞迴呼叫並快取結果。具體的遞歸推導可參考這個問題。注意對求出的加法子集內部進行了排序，最後進行並集操作以刪除重複項。用例：

subsetSum[{1, 2, 3, 4, 5}, 8]
> {{3, 5}, {1, 2, 5}, {1, 3, 4}}

這個給定的數字可能是本問題集合中的任意元素，所以用subsetSum遍歷集合中的每個元素，用它和剩下的元素嘗試組成加式。最後並刪除重複的組合，即為可能的全部加法子集了。

summationList[lst_List] := Union @@ Array[
   i \[Function] Map[Append[lst[[i]]] /* Sort,
     Select[subsetSum[Delete[lst, i], lst[[i]]], Length[#] > 1 &]],
   Length[lst]]

上面程式碼同樣進行了集合內部排序運算，因為把和加入集合時可能打亂順序。而且刪除了加數個數少於2個的情況。用例：

summationList[{1, 2, 3, 4, 5}]
> {{1, 2, 3}, {1, 3, 4}, {1, 4, 5}, {2, 3, 5}}

找互斥最大並集

得到加法子集後，用權重的set packing找出它們中互斥最大並集。用線性規劃語言描述就是

$$array{text{maximize} & sum{|s_i| x_i} & text{最大化並集中的元素個數} \ text{subject to} & sum {m_i x_i} leq 1 & text{選取的集合是互斥的} \ & x_i in {0, 1} & text{$x_i=1$則選擇集合$i$，否則放棄集合$i$}}$$

Mathematica有提供內建的LinearProgramming函數：

pickSumList[lst_List] := Module[{sumlst},
  sumlst = summationList[lst];
  Pick[sumlst,
   LinearProgramming[
    -Length /@ sumlst,
    Outer[MemberQ[#2, #1] & /* Boole, lst, sumlst, 1],
    ConstantArray[{1, -1}, Length[lst]],
    ConstantArray[{0, 1}, Length[sumlst]],
    Integers],
   1]]

測試

題主的例子：

隨機產生一個16個元素的集合。

用pickSumList找出結果，並高亮顯示作為和的元素：

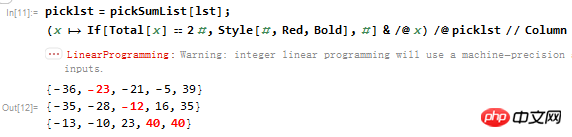
剩下的元素：

c++ - 如何实现去除所有集合内可以组成加法运算的子集

全部回覆(1)我來回復

找加法子集

找互斥最大並集

測試