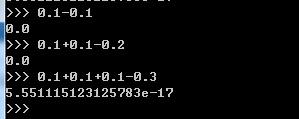
 python中如图的运算为什么结果接近零而不为零 是什么原因造成的? 浮点数缺乏精确性应该怎么解释? 为什么前两个运算式没出现问题 最后一个出现了问题? 请教
python中如图的运算为什么结果接近零而不为零 是什么原因造成的? 浮点数缺乏精确性应该怎么解释? 为什么前两个运算式没出现问题 最后一个出现了问题? 请教回复内容:
这是因为小数以二进制形式表示时的有穷性导致的。(下面的说法,不完全准确,只是帮助理解)以下是之前我在另一个地方对一个类似问题的解答,因为内容差不多,就直接搬过来了(本人略懒,希望有所帮助):
#################################此处开始####################################
我们知道,将一个小数转化为二进制表示的方式是,不断的乘2,取其中的整数部分。例如:
+----------------------------------------------------------------------------------------------------------------------------------+
(1) 0.625*2 = 1.25, 整数部分为1,小数部分为0.25
(2) 0.25 * 2 = 0.5 , 整数部分为0,小数部分为0.5
(3) 0.5 * 2 = 1 , 整数部分为1,小数部分为0
+----------------------------------------------------------------------------------------------------------------------------------+
所以0.625的二进制表示就是0.101。
然而有些小数,例如0.4,并不能够精确的转化为二进制表示,用上面的这种方法计算:
+----------------------------------------------------------------------------------------------------------------------------------+
(1) 0.4*2=0.8 整数部分为0,小数部分为0.8
(2) 0.8*2=1.6 整数部分为1,小数部分为0.6
(3) 0.6*2=1.2 整数部分为1,小数部分为0.2
(4) 0.2*2=0.4 整数部分为0,小数部分为0.4
(5) 0.4*2=0.8 整数部分为0,小数部分为0.8
(6) 0.8*2=1.6 整数部分为1,小数部分为0.6
(7) 0.6*2=1.2 整数部分为1,小数部分为0.2
……
+----------------------------------------------------------------------------------------------------------------------------------+
所以0.4转化为二进制,应该是0.0110... 这样一个无限循环小数。
计算机的内存、cpu寄存器等等这些硬件单元都是有限的,只能表示有限位数的二进制位,因此存储的二进制小数就会和实际转换而成的二进制数有一定的误差。(你可以试着将0.3转化为二进制表示,也将出现一个循环小数。)
实际上,大多数情况下,小数在计算机中是以一种类似科学计数法的形式表示的,具体的可以参考一下其他的资料。但即便如此,仍然存在误差。
所以在python中不建议直接将两个浮点数进行大小比较,或者做精确的计算,往往会得到意想不到的结果。当然,如果非要用,可以参考decimal模块的相关内容。 请将十进制数字0.1转换成二进制浮点数。 这不是Python的问题,而是实数的无限精度跟计算机的有限内存之间的矛盾。
举个例子,假如说我只能使用整数(即只精确到个位,计算机内的浮点数也只有有限精度,以C语言中的双精度浮点数double为例,精度为52个二进制位),要表示任意实数(无限精度)的时候我就只能通过舍入(rounding)来近似表示。
比如1.2我会表示成1,2.4表示成2,3.6表示成4.
所以呢?
在算1.2 - 1.2的时候,由于计算机表示的问题,我算的实际上是1 - 1,结果是0,碰巧蒙对了;
在算1.2 + 1.2 - 2.4的时候,由于计算机表示的问题,我算的实际上是1 + 1 - 2,结果是0,再次蒙对了;
但是在算1.2 + 1.2 + 1.2 - 3.6的时候,由于计算机表示的问题,我算的实际上是1 + 1 + 1 - 4,结果是-1,运气没那么好啦!
这里的1.2, 2.4, 3.6就相当于你问题里的0.1, 0.2和0.3,1, 2, 4则是真正在计算机内部进行运算的数值,我说清楚了吗?
其他请看IEEE 754浮点数标准,比如CSAPP第二章啥的(虽然估计你没兴趣看)。
另:不仅仅是浮点数的在计算机内部的表示有误差,运算本身也可能会有误差。比如整数2可以在计算机内准确表示,但是要算根号2就有误差了;再比如两个浮点数相除,本来两个数都是精确表示的,但除的结果精度却超出了计算机内实数的表示范围,然后就有误差了。 计算机智能处理可数集合的运算,但是全体实数是不可数的,所以计算机只能用一些奇怪的方法来拟合他,于是就产生了浮点数。 这个不是python 的问题,所有基于二进制的浮点数都会有这个问题,原因在于大部分浮点数转换为二进制后都是无限循环小数,而浮点数不可能用无限大的内存来储存,所以会有舍入的误差
详细可以看代码之谜(五) 来个 @vczh 答案的通俗版,比如用 10 个箱子装100个球,规定每个箱子只能装一个球,那显然是装不下所有球的。类似,double类型是 64bit 的,最多能表达 2^64 个数,实数有多少呢?无数个,所以 double 类型是装不下所有实数的,只能表达一个近似值。 9.4. decimal 计算机所有信息的存储使用二进制表示,像 @vczh 所说,有限的「位」,无法表示无数个数,那么,小数用二进制表示法,只能表示那些能被写成
 的数。
的数。0.1 的二进制表示为 0.000110011[0011]...,因为是无限循环的,无法用有限的位表示,所以计算机系统会进行舍入,以求用最接近的值来表示,这里涉及到不同的舍入方式,具体请见深入理解计算机系统,本答案也是参考该书。 大白话版的很多人都说了,就是计算机有限的数字表示不了数学中无穷的数。
楼主如果有一定计算机或者数学基础可以搜一下IEEE754,电脑是如何表示浮点数的一种协议。看懂了那个协议就知道为什么了~
如果看不懂IEEE754那就需要研究下数学中各种进制~主要是二进制、十进制和他们的关系。 自傲的人类!有本事你直接喂它2进制数,看看还有没有这种精度问题。
 python中兩個列表的串聯替代方案是什麼?May 09, 2025 am 12:16 AM
python中兩個列表的串聯替代方案是什麼?May 09, 2025 am 12:16 AM可以使用多種方法在Python中連接兩個列表:1.使用 操作符,簡單但在大列表中效率低;2.使用extend方法,效率高但會修改原列表;3.使用 =操作符,兼具效率和可讀性;4.使用itertools.chain函數,內存效率高但需額外導入;5.使用列表解析,優雅但可能過於復雜。選擇方法應根據代碼上下文和需求。
 Python:合併兩個列表的有效方法May 09, 2025 am 12:15 AM
Python:合併兩個列表的有效方法May 09, 2025 am 12:15 AM有多種方法可以合併Python列表:1.使用 操作符,簡單但對大列表不內存高效;2.使用extend方法,內存高效但會修改原列表;3.使用itertools.chain,適用於大數據集;4.使用*操作符,一行代碼合併小到中型列表;5.使用numpy.concatenate,適用於大數據集和性能要求高的場景;6.使用append方法,適用於小列表但效率低。選擇方法時需考慮列表大小和應用場景。
 編譯的與解釋的語言:優點和缺點May 09, 2025 am 12:06 AM
編譯的與解釋的語言:優點和缺點May 09, 2025 am 12:06 AMCompiledLanguagesOffersPeedAndSecurity,而interneterpretledlanguages provideeaseafuseanDoctability.1)commiledlanguageslikec arefasterandSecureButhOnderDevevelmendeclementCyclesclesclesclesclesclesclesclesclesclesclesclesclesclesclesclesclesclesandentency.2)cransportedeplatectentysenty
 Python:對於循環,最完整的指南May 09, 2025 am 12:05 AM
Python:對於循環,最完整的指南May 09, 2025 am 12:05 AMPython中,for循環用於遍歷可迭代對象,while循環用於條件滿足時重複執行操作。 1)for循環示例:遍歷列表並打印元素。 2)while循環示例:猜數字遊戲,直到猜對為止。掌握循環原理和優化技巧可提高代碼效率和可靠性。
 python concatenate列表到一個字符串中May 09, 2025 am 12:02 AM
python concatenate列表到一個字符串中May 09, 2025 am 12:02 AM要將列表連接成字符串,Python中使用join()方法是最佳選擇。 1)使用join()方法將列表元素連接成字符串,如''.join(my_list)。 2)對於包含數字的列表,先用map(str,numbers)轉換為字符串再連接。 3)可以使用生成器表達式進行複雜格式化,如','.join(f'({fruit})'forfruitinfruits)。 4)處理混合數據類型時,使用map(str,mixed_list)確保所有元素可轉換為字符串。 5)對於大型列表,使用''.join(large_li
 Python的混合方法:編譯和解釋合併May 08, 2025 am 12:16 AM
Python的混合方法:編譯和解釋合併May 08, 2025 am 12:16 AMpythonuseshybridapprace,ComminingCompilationTobyTecoDeAndInterpretation.1)codeiscompiledtoplatform-Indepententbybytecode.2)bytecodeisisterpretedbybythepbybythepythonvirtualmachine,增強效率和通用性。
 了解python的' for”和' then”循環之間的差異May 08, 2025 am 12:11 AM
了解python的' for”和' then”循環之間的差異May 08, 2025 am 12:11 AMtheKeyDifferencesBetnewpython's“ for”和“ for”和“ loopsare:1)” for“ loopsareIdealForiteringSequenceSquencesSorkNowniterations,而2)”,而“ loopsareBetterforConterContinuingUntilacTientInditionIntionismetismetistismetistwithOutpredefinedInedIterations.un
 Python串聯列表與重複May 08, 2025 am 12:09 AM
Python串聯列表與重複May 08, 2025 am 12:09 AM在Python中,可以通過多種方法連接列表並管理重複元素:1)使用 運算符或extend()方法可以保留所有重複元素;2)轉換為集合再轉回列表可以去除所有重複元素,但會丟失原有順序;3)使用循環或列表推導式結合集合可以去除重複元素並保持原有順序。


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

MantisBT
Mantis是一個易於部署的基於Web的缺陷追蹤工具,用於幫助產品缺陷追蹤。它需要PHP、MySQL和一個Web伺服器。請查看我們的演示和託管服務。

Atom編輯器mac版下載
最受歡迎的的開源編輯器

MinGW - Minimalist GNU for Windows
這個專案正在遷移到osdn.net/projects/mingw的過程中,你可以繼續在那裡關注我們。 MinGW:GNU編譯器集合(GCC)的本機Windows移植版本,可自由分發的導入函式庫和用於建置本機Windows應用程式的頭檔;包括對MSVC執行時間的擴展,以支援C99功能。 MinGW的所有軟體都可以在64位元Windows平台上運作。

Dreamweaver Mac版
視覺化網頁開發工具

禪工作室 13.0.1
強大的PHP整合開發環境






