JavaScript資料結構與演算法之圖與圖演算法_基礎知識

圖的定義

圖（Graph）是由頂點的有窮非空集合和頂點之間邊的集合組成，通常表示為：G(V,E)，其中，G表示一個圖，V是圖G中頂點的集合，E是圖G中邊的集合。

有向圖

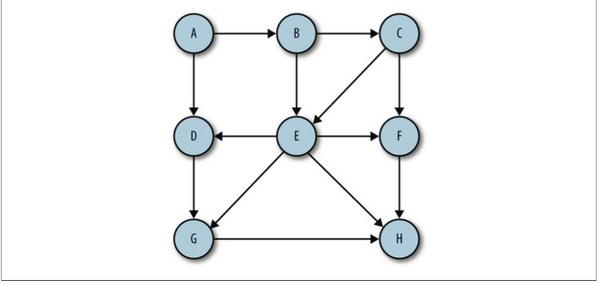
有向邊：若從頂點Vi到Vj的邊有方向，則稱這條邊為有向邊，也成為弧(Arc)，用有序偶來表示，Vi稱為弧尾，Vj稱為弧頭。

無序圖

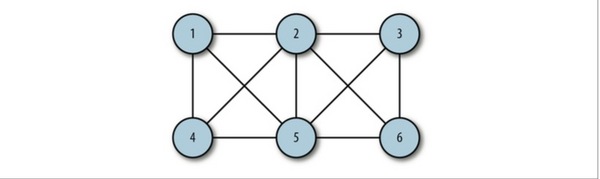
無向邊：若頂點Vi到Vj之間的邊沒有方向，則稱這條邊為無向邊(Edge)，用無序偶(Vi,Vj)來表示。

簡單圖

簡單圖：在圖結構中，若不存在頂點到其自身的邊，且同一條邊不重複出現，則稱這樣的圖為簡單圖。

圖類

表示頂點

建立圖類的第一步就是要建立一個Vertex類別來保存頂點和邊。這個類別的作用和鍊錶、二元搜尋樹的Node類別一樣。 Vertex類別有兩個資料成員：一個用來識別頂點，另一個表示是否被存取過的布林值。分別被命名為label和wasVisited。

複製程式碼 程式碼如下:

function Vertex(label){
    this.label = label;
}

我們將所有頂點保存在數組中，在圖類裡，可以透過他們在數組中的位置引用他們

表示邊

圖的實際資訊都保存在「邊」上面，因為他們描述了圖的結構。二元樹的一個父節點只能有兩個子節點，而圖的結構卻要靈活得多，一個頂點既可以有一條邊，也可以有多條邊和它相連。

我們將表示圖的邊的方法成為鄰接表或鄰接表數組。它將儲存由頂點的相鄰頂點列表構成的數組

建構圖

定義如下一個Graph類：

複製程式碼 程式碼如下:

function Graph(v){
    this.vertices = v;//vertices至高點
    this.edges = 0;
    this.adj = [];
    for(var i =0;I         this.adj[i] = [];
        this.adj[i].push('');
    }
    this.addEdge = addEdge;
    this.toString = toString;
}

這個類別會記錄一個圖表示了多少邊，並使用一個長度與圖的頂點數來記錄頂點的數量。

複製程式碼 程式碼如下:

function addEdge(){
    this.adj[v].push(w);
    this.adj[w].push(v);
    this.edges ;
}

這裡我們使用for迴圈為陣列中的每個元素新增一個子陣列來儲存所有的相鄰頂點，並將所有元素初始化為空字串。

圖的遍歷

深度優先遍歷

深度優先遍歷(DepthFirstSearch)，也有稱為深度優先搜索，簡稱DFS。

例如在一個房間內尋找一把鑰匙，無論從哪一間房間開始都可以，將房間內的牆角、床頭櫃、床上、床下、衣櫃、電視櫃等挨個尋找，做到不放過任何一個死角，當所有的抽屜、儲藏櫃中全部都找遍後，接著再尋找下一個房間。

深度優先搜尋：

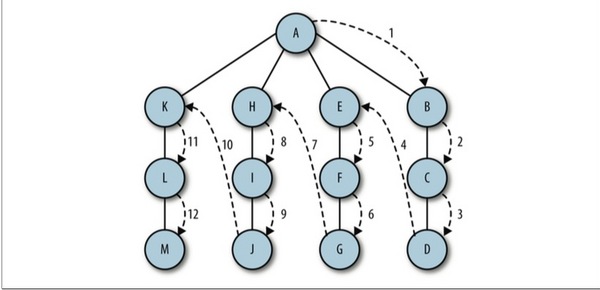
深度優先搜尋就是訪問一個沒有訪問過的頂點，將他標記為已訪問，再遞歸地去訪問在初始頂點的鄰接表中其他沒有訪問過的頂點

為Graph類別新增一個陣列：

複製程式碼 程式碼如下:

this.marked = [];//儲存已造訪過的頂點
for(var i=0;i     this.marked[i] = false;//初始化為false
}

深度優先搜尋函數：

複製程式碼 程式碼如下:

function dfs(v){
    this.marked[v] = true;
    //if語句在這裡不是必須的
    if(this.adj[v] != undefined){
        print("Visited vertex: " v );
        for each(var w in this.adj[v]){
            if(!this.marked[w]){
                this.dfs(w);
            }
        }
    }
}

廣度優先搜尋

廣度優先搜尋（BFS）屬於一種盲目搜尋法，目的是系統地展開並檢查圖中的所有節點，以尋找結果。換句話說，它並不考慮結果的可能位置，徹底搜尋整張圖，直到找到結果為止。

廣度優先搜尋從第一個頂點開始，盡量存取盡可能靠近它的頂點，如下圖所示：

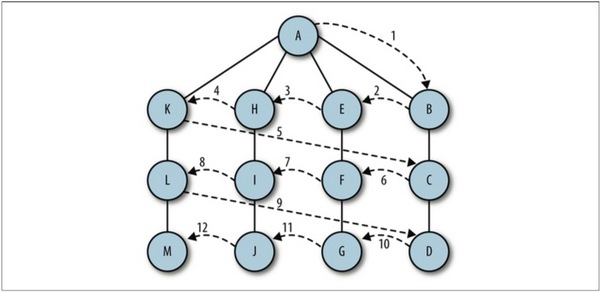
其工作原理為：

 1. 首先尋找與目前頂點相鄰的未存取的頂點，將其新增至已存取頂點清單及佇列；
 2. 然後從圖中取出下一個頂點v，加入到已訪問的頂點列表
 3. 最後將所有與v相鄰的未存取頂點加入佇列
以下是廣度優先搜尋函數的定義：

複製程式碼 程式碼如下:

function bfs(s){
    var queue = [];
    this.marked = true;
    queue.push(s);//加到隊尾
    while(queue.length>0){
        var v = queue.shift();//從隊首移除
        if(v == undefined){
            print("Visited vertex: " v);
        }
        for each(var w in this.adj[v]){
            if(!this.marked[w]){
                this.edgeTo[w] = v;
                this.marked[w] = true;
                queue.push(w);
            }
        }
    }
}

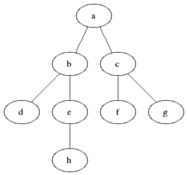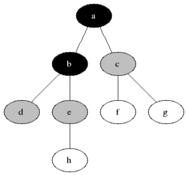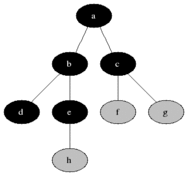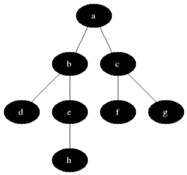
最短路徑

執行廣度優先搜尋時，會自動尋找從一個頂點到另一個相連頂點的最短路徑

確定路徑

要找出最短路徑，需要修改廣度優先搜尋演算法來記錄從一個頂點到另一個頂點的路徑，我們需要一個陣列來保存從一個頂點操下一個頂點的所有邊，我們將這個陣列命名為edgeTo

複製程式碼 程式碼如下:

this.edgeTo = [];//將這行加入Graph類別

//bfs函數
function bfs(s){
    var queue = [];
    this.marked = true;
    queue.push(s);//加到隊尾
    while(queue.length>0){
        var v = queue.shift();//從隊首移除
        if(v == undefined){
            print("Visited vertex: " v);
        }
        for each(var w in this.adj[v]){
            if(!this.marked[w]){
                this.edgeTo[w] = v;
                this.marked[w] = true;
                queue.push(w);
            }
        }
    }
}

拓樸排序演算法

拓樸排序會對有向圖的所有頂點進行排序，使有向邊從前面的頂點指向後面的頂點。
拓樸排序演算法與BFS類似，不同的是，拓樸排序演算法不會立即輸出已存取的頂點，而是存取目前頂點鄰接表中的所有相鄰頂點，直到這個清單窮盡時，才會將目前頂點壓入棧中。

拓樸排序演算法被分割為兩個函數，第一個函數是topSort()，用來設定排序程序並呼叫一個輔助函數topSortHelper()，然後顯示排序好的頂點列表

拓撲排序演算法主要工作是在遞歸函數topSortHelper()中完成的，這個函數會將當前頂點標記為已訪問，然後遞歸訪問當前頂點鄰接表中的每個頂點，標記這些頂點為已訪問。最後，將目前頂點壓入堆疊中。

複製程式碼 程式碼如下:

//topSort()函數
function topSort(){
    var stack = [];
    var visited = [];
    for(var i =0;i         visited[i] = false;
    }
    for(var i = 0;i         if(visited[i] == false){
            this.topSortHelper(i,visited,stack);
        }
    }
    for(var i = 0;i         if(stack[i] !=undefined && stack[i] != false){
            print(this.vertexList[stack[i]]);
        }
    }
}

//topSortHelper()函數
function topSortHelper(v,visited,stack){
    visited[v] = true;
    for each(var w in this.adj[v]){
        if(!visited[w]){
            this.topSortHelper(visited[w],visited,stack);
        }
    }
    stack.push(v);
}