MLP一夜被幹掉！ MIT加州理工等革命性KAN破紀錄，發現數學定理碾壓DeepMind

一夕之間，機器學習範式要變天了！

當今，統治深度學習領域的基礎架構就是，多層感知器（MLP）－將活化函數放置在神經元上。

那麼，除此之外，我們是否還有新的路線可以走？

就在今天，來自MIT、加州理工學院、東北大學等機構的團隊重磅發布了，全新的神經網路結構－Kolmogorov–Arnold Networks（KAN）。

研究人員對MLP做了一個簡單的改變，即將可學習的活化函數從節點（神經元）移到邊（權重）上！

論文網址：https://arxiv.org/pdf/2404.19756

##這個改變乍一聽似乎毫無根據，但它與數學中的「逼近理論」（approximation theories）有著相當深刻的聯繫。

事實證明，Kolmogorov-Arnold表示對應兩層網絡，在邊上，而非節點上，有可學習的激活函數。

正是從表示定理得到啟發，研究者用神經網路顯式地，將Kolmogorov-Arnold表示參數化。

值得一提的是，KAN名字的由來，是為了紀念兩位偉大的已故數學家Andrey Kolmogorov和Vladimir Arnold。

實驗結果顯示，KAN比傳統的MLP有更優越的效能，提升了神經網路的準確性和可解釋性。

而最令人意想不到的是，KAN的視覺化和互動性，讓其在科學研究中具有潛在的應用價值，能夠幫助科學家發現新的數學和物理規律。

研究中，作者用KAN重新發現了紐結理論（knot theory）中的數學定律！

而且，KAN以更小的網路和自動化方式，復現了DeepMind在2021年的結果。

在物理方面，KAN可以幫助物理學家研究Anderson局域化（這是凝聚態物理中的一種相變）。

對了，順便提一句，研究中KAN的所有範例（除了參數掃描），在單一CPU上不到10分鐘就可以復現。

KAN的橫空出世，直接挑戰了一直以來統治機器學習領域的MLP架構，在全網掀起軒然大波。

機器學習新紀元開啟

有人直呼，機器學習的新紀元開始了！

#

GoogleDeepMind研究科學家稱，「Kolmogorov-Arnold再次出擊！一個鮮為人知的事實是：這個定理出現在一篇關於置換不變神經網路（深度集）的開創性論文中，展示了這種表示與集合/GNN聚合器建構方式（作為特例）之間的複雜聯繫」。

一個全新的神經網路架構誕生了！ KAN將大幅改變人工智慧的訓練和微調方式。

難道是AI進入了2.0時代？

還有網友用通俗的語言，將KAN和MLP的區別，做了一個形象的比喻：

Kolmogorov-Arnold網路（KAN）就像一個可以烤任何蛋糕的三層蛋糕配方，而多層感知器（MLP）是一個有不同層數的客製化蛋糕。 MLP更複雜但更通用，而KAN是靜態的，但針對一項任務更簡單、更快速。

論文作者，MIT教授Max Tegmark表示，最新論文表明，一種與標準神經網路完全不同的架構，在處理有趣的物理和數學問題時，以更少的參數實現了更高的精度。

接下來，一起來看看代表深度學習未來的KAN，是如何實現的？

重回牌桌上的KAN

KAN的理論基礎

柯爾莫哥洛夫-阿諾德定理（Kolmogorov–Arnold representation theorem）指出，如果f是定義在有界域上的多變量連續函數，那麼該函數就可以表示為多個單變量、加法連續函數的有限組合。

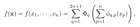
對於機器學習來說，問題可以描述為：學習高維函數的過程可以簡化成學習多項式數量的一維函數。

但這些一維函數可能是非光滑的，甚至是分形的（fractal），在實踐中可能無法學習，也正是由於這種「病態行為」，柯爾莫哥洛夫-阿諾德表示定理在機器學習領域基本上被判了「死刑」，即理論正確，但實際上無用。

在這篇文章中，研究人員仍然對該定理在機器學習領域的應用持樂觀態度，並提出了兩點改進：

1、原始方程式中，只有兩層非線性和一個隱藏層（2n 1），可以將網路泛化到任意寬度和深度；

2、科學和日常生活中的大多數函數大多是光滑的，並且具有稀疏的組合結構，可能有助於形成平滑的柯爾莫哥洛夫-阿諾德表示。類似於物理學家和數學家的區別，物理學家更關注典型場景，而數學家更關心最壞情況。

KAN架構

柯爾莫哥洛夫-阿諾德網路（KAN）設計的核心思想是將多變量函數的逼近問題轉化為學習一組單變數函數的問題。在這個框架下，每個單變數函數可以用B樣條曲線來參數化，其中B樣條是一種局部的、分段的多項式曲線，其係數是可學習的。

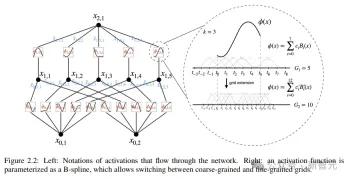
為了把原始定理中的兩層網路擴展到更深、更寬，研究人員提出了一個更「泛化」的定理版本來支援設計KAN：

受MLPs層疊結構來提升網路深度的啟發，文中同樣引入了一個類似的概念，KAN層，由一個一維函數矩陣組成，每個函數都有可訓練的參數。

根據柯爾莫哥洛夫-阿諾德定理，原始的KAN層由內部函數和外部函數組成，分別對應於不同的輸入和輸出維度，這種堆疊KAN層的設計方法不僅擴展了KANs的深度，而且保持了網路的可解釋性和表達能力，其中每個層都是由單變量函數組成的，可以對函數進行單獨學習和理解。

下式中的f就等價於KAN

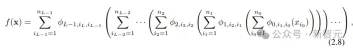
實作細節

雖然KAN的設計概念看起來簡單，純靠堆疊，但優化起來也不容易，研究人員在訓練過程中也摸索到了一些技巧。

1、殘差激活函數：透過引入基底函數b(x)和樣條函數的組合，使用殘差連接的概念來建構激活函數ϕ(x)，有助於訓練過程的穩定性。

2、初始化尺度（scales）：啟動函數的初始化設定為接近零的樣條函數，權重w使用Xavier初始化方法，有助於在訓練初期保持梯度的穩定。

3、更新樣條網格：由於樣條函數定義在有界區間內，而神經網路訓練過程中活化值可能會超出這個區間，因此動態更新樣條網格可以確保樣條函數始終在適當的區間內運作。

參數量

1、網路深度：L

2、每層的寬度：N

3、每個樣條函數是基於G個區間（G 1個網格點）定義的，k階（通常k=3）

所以KANs的參數量約為

作為對比，MLP的參數量為O(L*N^2)，看起來比KAN效率更高，但KANs可以使用更小的層寬度（N），不僅可以提升泛化性能，還能提升可解釋性。

KAN比MLP，勝在了哪？

表現更強

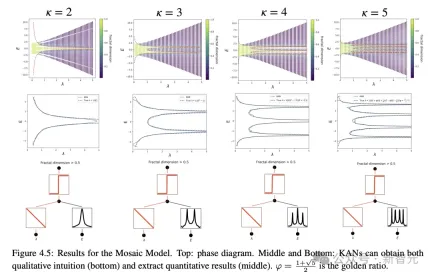
作為合理性檢驗，研究人員建構了五個已知具有平滑KA（柯爾莫哥洛夫-阿諾德）表示的例子作為驗證資料集，透過每200步增加網格點的方式對KANs進行訓練，涵蓋G的範圍為{3,5,10,20,50,100,200,500,1000}

#使用不同深度和寬度的MLPs作為基準模型，並且KANs和MLPs都使用LBFGS演算法總共訓練1800步，再用RMSE作為指標進行比較。

#

從結果可以看到，KAN的曲線更抖，能夠快速收斂，達到平穩狀態；並且比MLP的縮放曲線更好，尤其是在高維的情況下。

也可以看到，三層KAN的表現要遠遠強於兩層，顯示更深的KANs具有更強的表達能力，符合預期。

互動解釋KAN

研究人員設計了一個簡單的迴歸實驗，以展現使用者可以在與KAN的互動過程中，獲得可解釋性最強的結果。

假設使用者對於找出符號公式感興趣，總共需要經過5個互動步驟。

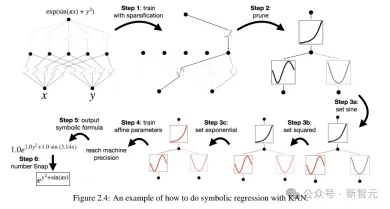
步驟 1：有稀疏化的訓練。

從全連接的KAN開始，透過帶有稀疏化正則化的訓練可以使網路變得更稀疏，從而可以發現隱藏層中，5個神經元中的4個都看起來沒什麼作用。

步驟2：剪枝

自動剪枝後，丟棄掉所有無用的隱藏神經元，只留下一個KAN，把激活函數匹配到已知的符號函數。

步驟3：設定符號函數

假設使用者可以正確地從盯著KAN圖表猜測出這些符號公式，就可以直接設定

如果使用者沒有領域知識或不知道這些激活函數可能是哪些符號函數，研究人員提供了一個函數suggest_symbolic來建議符號候選項。

步驟4：進一步訓練

在網路中所有的激活函數都符號化之後，唯一剩下的參數就是仿射參數；繼續訓練仿射參數，當看到損失降到機器精度（machine precision）時，就能意識到模型已經找到了正確的符號表達式。

步驟 5：輸出符號公式

#使用Sympy計算輸出節點的符號公式，驗證正確答案。

可解釋性驗證

研究人員首先在一個有監督的玩具資料集中，設計了六個樣本，展現KAN網路在符號公式下的組合結構能力。

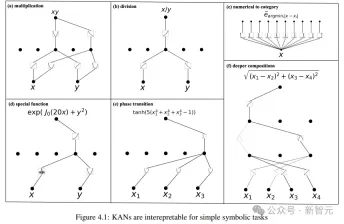
可以看到，KAN成功學習到了正確的單變數函數，並透過視覺化的方式，可解釋地展現出KAN的思考過程。

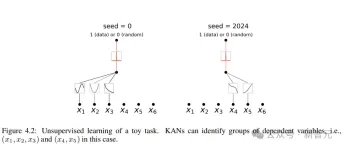
在無監督的設定下，資料集中只包含輸入特徵x，透過設計某些變數（x1, x2, x3）之間的聯繫，可以測試出KAN模型尋找變數之間依賴關係的能力。

從結果來看，KAN模型成功找到了變數之間的函數依賴性，但作者也指出，目前仍然只是在合成數據上進行實驗，還需要更有系統、更可控的方法來發現完整的關係。

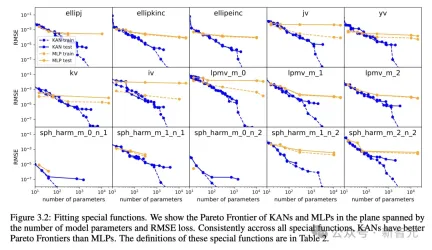
帕累托最適

#透過擬合特殊函數，作者展示了KAN和MLP在由模型參數數量和RMSE損失跨越的平面中的帕累托前緣（Pareto Frontier）。

在所有特殊函數中，KAN總是比MLP有更好的帕累托前緣。

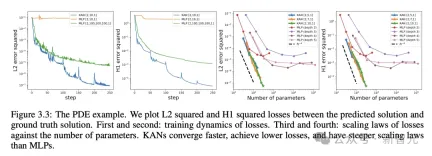
求解偏微方程式

#在求解偏微方程式任務中，研究者繪製了預測解和真實解之間的L2平方和H1平方損失。

下圖中，前兩個是損失的訓練動態，第三和第四是損失函數數的擴展定律（Sacling Law）。

如下結果所示，與MLP相比，KAN的收斂速度更快，損失更低，並且具有更陡峭的擴展定律。

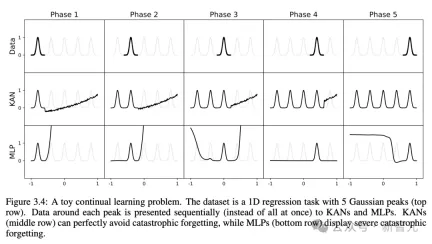
持續學習，不會發生災難性遺忘

我們都知道，災難性遺忘是機器學習中，一個嚴重的問題。

人工神經網路和大腦之間的差異在於，大腦具有放置在空間局部功能的不同模組。當學習新任務時，結構重組僅發生在負責相關技能的局部區域，而其他區域則保持不變。

然而，大多數人工神經網絡，包括MLP，卻沒有這種局部性概念，這可能是災難性遺忘的原因。

而研究證明了，KAN具有局部可塑性，並且可以利用樣條（splines）局部性，來避免災難性遺忘。

這個想法非常簡單，由於樣條是局部的，樣本只會影響一些附近的樣條係數，而遠處的係數保持不變。

相較之下，由於MLP通常使用全域活化（如ReLU/Tanh/SiLU），因此，任何局部變化都可能不受控制地傳播到遠處的區域，從而破壞儲存在那裡的資訊。

研究人員採用了一維回歸任務（由5個高斯峰組成）。每個峰值周圍的資料按順序（而不是一次全部）呈現給KAN和MLP。

結果如下圖所示，KAN僅重構目前階段存在資料的區域，而使先前的區域保持不變。

而MLP在看到新的資料樣本後會重塑整個區域，導致災難性的遺忘。

發現紐結理論，結果超越DeepMind

KAN的誕生對於機器學習未來應用，意味著什麼？

紐結理論（Knot theory）是低維拓撲學中的一門學科，它揭示了三流形和四流形的拓撲問題，並在生物學和拓撲量子計算等領域有著廣泛的應用。

2021年，DeepMind團隊曾首次以AI證明了紐結理論（knot theory）登上了Nature。

論文網址：https://www.nature.com/articles/s41586-021-04086-x

#這項研究中，透過監督學習和人類領域專家，得出了一個與代數和幾何結不變量相關的新定理。

即梯度顯著性識別出了監督問題的關鍵不變量，這使得領域專家提出了一個猜想，隨後得到了完善和證明。

對此，作者研究KAN是否可以在同一問題上取得良好的可解釋結果，從而預測紐結的簽名。

在DeepMind實驗中，他們研究紐結理論資料集的主要結果是：

1  利用網路歸因法發現，簽章主要取決於中間距離和縱向距離λ。

2 人類領域專家後來發現與斜率有很高的相關性並得到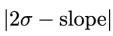

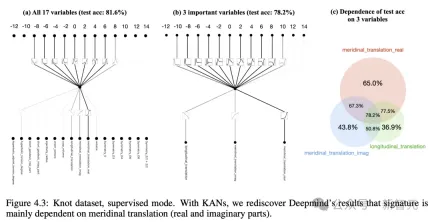
為了研究問題（1），作者將17個紐結不變量視為輸入，將簽章視為輸出。

與DeepMind中的設定類似，簽名（偶數）被編碼為一熱向量，並且網路透過交叉熵損失進行訓練。

結果發現，一個極小的KAN能夠達到81.6%的測試精度，而DeepMind的4層寬度300MLP，僅達到78%的測試精度。

如下表所示，KAN (G = 3, k = 3) 有約200參數，而MLP約有300000參數量。

值得注意的是，KAN不僅更準確，而且更準確。同時比MLP的參數效率更高。

在可解釋性方面，研究人員根據每個活化的大小來縮放其透明度，因此無需特徵歸因即可立即清楚，哪些輸入變數是重要的。

然後，在三個重要變數上訓練KAN，獲得78.2%的測試準確率。

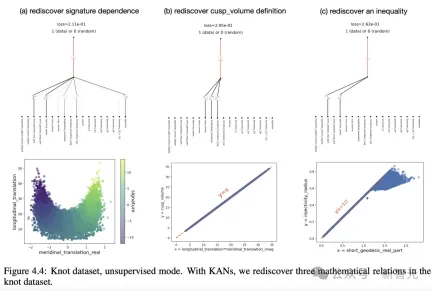
如下是，透過KAN，作者重新發現了紐結資料集中的三個數學關係。

物理Anderson局域化有解了

而在物理應用中，KAN也發揮了巨大的價值。

Anderson是一種基本現象，其中量子系統中的無序會導致電子波函數的局域化，從而使所有傳輸停止。

在一維和二維中，尺度論證表明，對於任何微小的隨機無序，所有的電子本徵態都呈指數級局域化。

相較之下，在三維中，一個臨界能量形成了一個相分界，將擴展態和局域態分開，稱為移動性邊緣。

理解這些移動性邊緣對於解釋固體中的金屬-絕緣體轉變等各種基本現象至關重要，以及在光子設備中光的局域化效應。

作者透過研究發現，KANs使得提取移動性邊緣變得非常容易，無論是數值上的，還是符號上的。

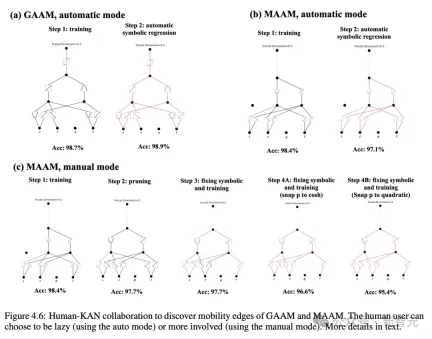
顯然，KAN已然成為科學家的得力助手、重要的合作者。

總而言之，得益於準確性、參數效率和可解釋性的優勢，KAN將是AI Science一個有用的模型/工具。

未來，KAN的進一步在科學領域的應用，仍有待挖掘。

以上是MLP一夜被幹掉！ MIT加州理工等革命性KAN破紀錄，發現數學定理碾壓DeepMind的詳細內容。更多資訊請關注PHP中文網其他相關文章！