在陶哲軒的啟發下,越來越多的數學家開始嘗試利用人工智慧進行數學探索。這次,他們瞄準的目標是世界十大最頂尖數學難題之一的費馬大定理。費馬大定理是一個非常複雜的數學難題,迄今尚未找到可行的解法。數學家希望藉助人工智慧的強大運算能力和智慧演算法,能夠在數學中探索

費馬大定理又被稱為「費馬最後的定理(Fermat's Last Theorem,FLT)”,由17世紀法國數學家皮耶・德・費馬提出。它背後有一個傳奇的故事。據稱,大約在1637年左右,費馬在閱讀丟番圖《算術》拉丁文譯本時,曾在第11卷第8命題旁寫道:「將一個立方數分成兩個立方數之和,或一個四次冪分成兩個四次冪之和,或一般地將一個高於二次方的冪分成兩個同次方之和,這是不可能的。種美妙的證法,可惜這裡空白的地方太小,寫不下了。 」

這段話前面所表述的就是費馬大定理的內容:當整數n>2 時,關於x^n y^n=z^n 的方程沒有正整數解。 ,後世是有爭議的。孤軍奮戰,終於用130頁長的篇幅完成了證明。還能用AI 做什麼呢?定理和證明,使其能夠在計算機上進行表示、驗證和操作,從而保證數學內容的準確性和一致性。始於20世紀的數理邏輯和計算機科學的發展。 形式化數學的主要目標是建立一套形式系統,其中包括一組符號、一組基本公理和一組推理規則,透過這些規則和公理的運用,可以進行
去年年底,陶哲軒等人曾用Lean(一款互動式定理證明器,也是一門程式語言)形式化了他們的一篇論文。這篇論文是對多項式 Freiman-Ruzsa 猜想的一個版本的證明,於去年 11 月發佈在 arXiv 上。在編寫 Lean 語言程式碼的時候,陶哲軒也藉助了 AI 程式設計助手 Copilot。這事件引起數學界和人工智慧界的廣泛關注。
當時,Lean 技術開源社群最重要的推廣者、倫敦帝國學院的Kevin Buzzard 表示:「從根本上來說,顯而易見的是,當你將某些東西數位化時,你就可以以新的方式使用它。的工具也是Lean。
在一篇部落格中,他介紹了自己做這件事情的背景、動機以及具體的做法。
為什麼要形式化費馬大定理的證明?費馬大定理的形式非常簡潔、直觀,然而證明它卻異常艱難。這無疑是數學深邃之美的絕佳展示。在過去的幾個世紀中,為了解決這個問題,數學家們發展和創新了大量數學理論,這些理論在密碼學到物理學等多個領域都有所應用。
Andrew Wiles 可能因FLT 而受到啟發,但他的工作實際上為朗蘭茲計劃帶來了突破,該計劃是數學中一系列影響深遠的構想,聯繫數論、代數幾何與約化群表示理論,且在2024 年依然備受關注。
歷史上,代數數論的其他幾個重大突破(例如數域中的因式分解理論和循環域的算術)至少部分是出於對 FLT 更深層理解的渴望。 
Wiles 的工作,由他的學生 Richard Taylor 一起補充完整,建立在 20 世紀數學的龐大基礎之上。 Wiles 引入的基本技術 ——「模性提升定理(modularity lifting theorem)」—— 在原始論文發表後的 30 年間,在概念上被極大簡化和廣泛推廣。這一領域至今仍然非常活躍。 Frank Calegari 在 2022 年國際數學家大會上的論文,概述了自 Wiles 突破以來的進展(參見:https://arxiv.org/abs/2109.14145)。 Kevin Buzzard 表示,這一領域的持續活躍,是他將 FLT 證明形式化的動機之一。
數學的形式化,將紙上的數學轉換成能夠理解定理和證明概念的電腦程式語言的藝術。這些程式語言,也稱為互動式定理證明器(ITP),已經存在了數十年。然而,近年來,這一領域似乎吸引了數學界的一部分關注。我們見證了多個研究數學形式化的例子,其中最新的是陶哲軒等人對多項式 Freiman—Ruzsa 猜想證明的形式化。這篇 2023 年的突破性論文在短短三週內就在 Lean 中完成了形式化。這樣的成功案例可能會讓旁觀者認為,像 Lean 這樣的 ITP 現在已經準備好形式化所有現代數學了。
然而,真相遠非如此簡單。在數學的某些領域,例如組合學,我們可以看到一些現代突破可以即時形式化。然而,Buzzard 表示,他定期參加倫敦數論研討會,經常注意到 Lean 對現代數學定義的了解還不足以表達研討會上宣布的結果,更不用說驗證它們的證明了。
事實上,數論在這一方面的「滯後」是 Buzzard 啟動 FLT 當代證明形式化的主要動機之一。在專案完成之前,Lean 將能夠理解自守形式(一類特別的複變量函數)和表示、伽羅瓦表示、潛在自守性、模性提升定理、代數簇的算術、類域論、算術對偶定理、志村簇等現代代數數論所使用的概念。在 Buzzard 看來,有了這些做基礎,將他自己專業領域正在發生的事情形式化將不再是科幻小說。
那麼,為什麼要這麼做呢? Buzzard 解釋說,「如果我們相信一些電腦科學家的話,人工智慧的指數級增長終將使電腦能夠幫助數學家進行研究。這樣的工作可以幫助電腦理解我們在現代數學研究中正在做的事情。」
專案如何進行?
費馬大定理的形式化計畫現已啟動。 Buzzard 在一幅圖中展示了當前的進展。
有興趣的研究者可以閱讀詳情:https://imperialcollegelondon.github.io/FLT/blueprint/dep_graph_document.html
該專案由EPSRC 資助,Buzzard 將獲得前五年的資金支持。在此期間,他的第一個目標是將 FLT 簡化為 1980 年代末數學家已知的聲明。
當然,Buzzard 沒有打算獨自完成這件事。他表示,對於有些論證的部分,他理解其基本原則,但從未仔細檢查過細節。而且,朗蘭茲計劃還引入了一些重要的東西,包括 GL_2 的循環基變換以及 Jacquet-Langlands。對於這些深奧的東西,他的理解還不夠深。
不過,這正是形式化專案的優勢所在。 Buzzard 將能夠在 Lean 中明確表達他需要的結果,並將它們傳遞給其他人。這個系統的美妙之處在於:你不必理解 FLT 的整個證明就能做出貢獻。上面的圖將證明分解為許多小引理,因此非常方便進行眾包操作。如果你能形式化證明其中任何一個引理,那麼 Buzzard 會熱切期待你的拉取請求。
想要參與專案的人需要了解一些關於 Lean 的知識。對此,Buzzard 推薦了線上教科書 Mathematics in Lean。
教科書連結:https://leanprover-community.github.io/mathematics_in_lean/
該專案將在Lean Zulip chat 的FLT stream 上進行,這是一個強大的研究論壇,數學家和電腦科學家可以即時協作,輕鬆地發布程式碼和數學,使用線程和stream 系統,有效地支援多場獨立對話同時進行。
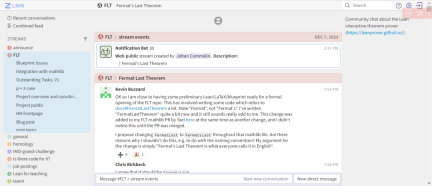
Lean Zulip chat 連結:https://leanprover.zulipchat.com/
Buzzard 表示,他對這個專案將需要多長時間沒有任何預感,但他絕對樂觀。
同時,像 Lean 這類形式化證明工具也在不斷迭代。相較於初代 Lean,現在最新的 Lean 4 版本進行了多項最佳化,包括更快的編譯器、改進的錯誤處理和更好的與外部工具整合的能力等。
去年年底,開放平台LeanDojo 團隊和加州理工學院的研究者也推出了Lean Copilot,這是一款專為大型語言模型與人類互動而設計的協作工具,為數學研究注入了AI大模型的力量。
「我預計,如果使用得當,到 2026 年,AI 將成為數學研究和許多其他領域值得信賴的合著者。」陶哲軒在之前的部落格中說道。
希望陶哲軒的預言早日成真。
相關閱讀:
#參考連結:https://leanprover.zulipchat.com/#narrow/stream/416277-FLT
https: //mp.weixin.qq.com/s/d9RSkRhlKH5ZMek3yTqe4Q
#以上是跨越300多年的接力:受陶哲軒啟發,數學家決定用AI形式化費馬大定理的證明的詳細內容。更多資訊請關注PHP中文網其他相關文章!
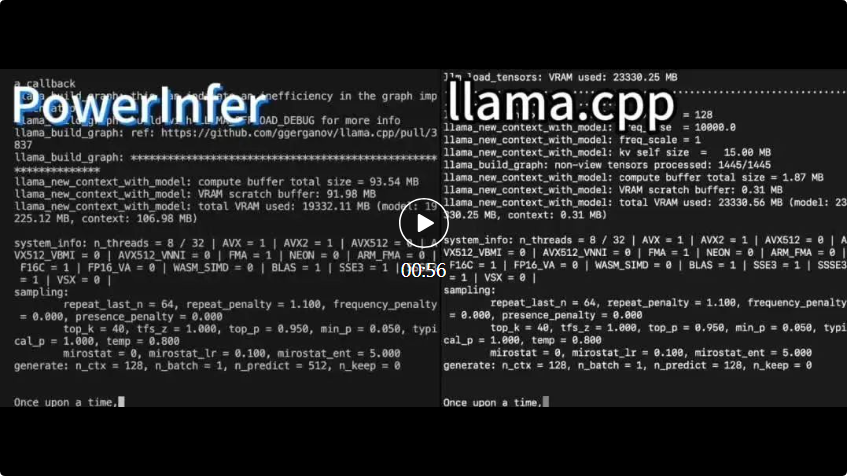 4090生成器:与A100平台相比,token生成速度仅低于18%,上交推理引擎赢得热议Dec 21, 2023 pm 03:25 PM
4090生成器:与A100平台相比,token生成速度仅低于18%,上交推理引擎赢得热议Dec 21, 2023 pm 03:25 PMPowerInfer提高了在消费级硬件上运行AI的效率上海交大团队最新推出了超强CPU/GPULLM高速推理引擎PowerInfer。PowerInfer和llama.cpp都在相同的硬件上运行,并充分利用了RTX4090上的VRAM。这个推理引擎速度有多快?在单个NVIDIARTX4090GPU上运行LLM,PowerInfer的平均token生成速率为13.20tokens/s,峰值为29.08tokens/s,仅比顶级服务器A100GPU低18%,可适用于各种LLM。PowerInfer与
 思维链CoT进化成思维图GoT,比思维树更优秀的提示工程技术诞生了Sep 05, 2023 pm 05:53 PM
思维链CoT进化成思维图GoT,比思维树更优秀的提示工程技术诞生了Sep 05, 2023 pm 05:53 PM要让大型语言模型(LLM)充分发挥其能力,有效的prompt设计方案是必不可少的,为此甚至出现了promptengineering(提示工程)这一新兴领域。在各种prompt设计方案中,思维链(CoT)凭借其强大的推理能力吸引了许多研究者和用户的眼球,基于其改进的CoT-SC以及更进一步的思维树(ToT)也收获了大量关注。近日,苏黎世联邦理工学院、Cledar和华沙理工大学的一个研究团队提出了更进一步的想法:思维图(GoT)。让思维从链到树到图,为LLM构建推理过程的能力不断得到提升,研究者也通
 复旦NLP团队发布80页大模型Agent综述,一文纵览AI智能体的现状与未来Sep 23, 2023 am 09:01 AM
复旦NLP团队发布80页大模型Agent综述,一文纵览AI智能体的现状与未来Sep 23, 2023 am 09:01 AM近期,复旦大学自然语言处理团队(FudanNLP)推出LLM-basedAgents综述论文,全文长达86页,共有600余篇参考文献!作者们从AIAgent的历史出发,全面梳理了基于大型语言模型的智能代理现状,包括:LLM-basedAgent的背景、构成、应用场景、以及备受关注的代理社会。同时,作者们探讨了Agent相关的前瞻开放问题,对于相关领域的未来发展趋势具有重要价值。论文链接:https://arxiv.org/pdf/2309.07864.pdfLLM-basedAgent论文列表:
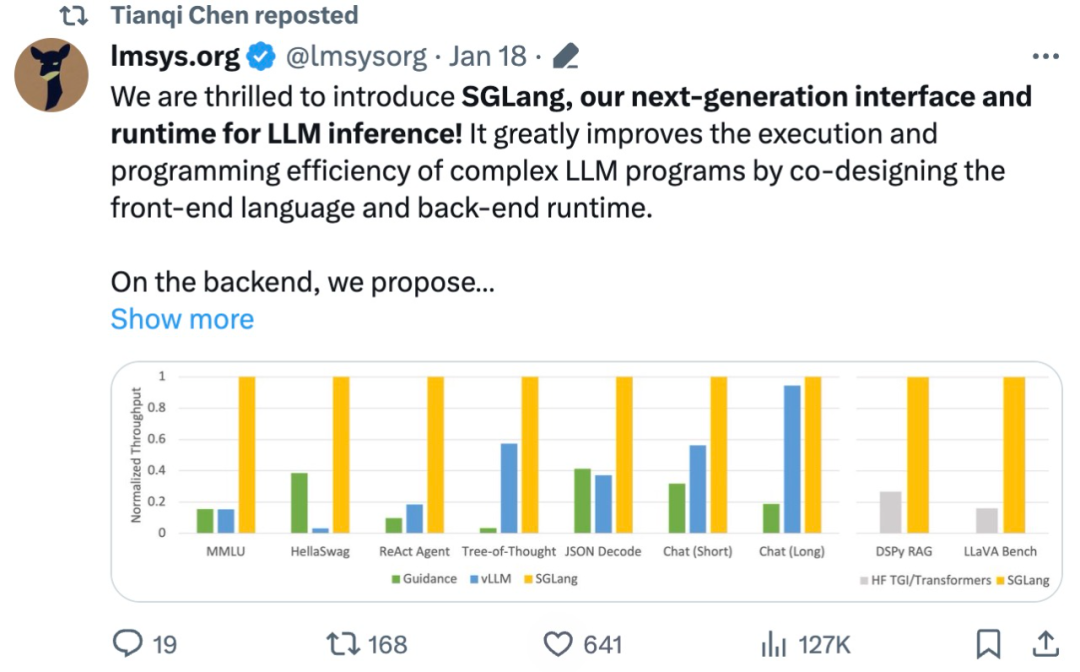 吞吐量提升5倍,联合设计后端系统和前端语言的LLM接口来了Mar 01, 2024 pm 10:55 PM
吞吐量提升5倍,联合设计后端系统和前端语言的LLM接口来了Mar 01, 2024 pm 10:55 PM大型语言模型(LLM)被广泛应用于需要多个链式生成调用、高级提示技术、控制流以及与外部环境交互的复杂任务。尽管如此,目前用于编程和执行这些应用程序的高效系统却存在明显的不足之处。研究人员最近提出了一种新的结构化生成语言(StructuredGenerationLanguage),称为SGLang,旨在改进与LLM的交互性。通过整合后端运行时系统和前端语言的设计,SGLang使得LLM的性能更高、更易控制。这项研究也获得了机器学习领域的知名学者、CMU助理教授陈天奇的转发。总的来说,SGLang的
 大模型也有小偷?为保护你的参数,上交大给大模型制作「人类可读指纹」Feb 02, 2024 pm 09:33 PM
大模型也有小偷?为保护你的参数,上交大给大模型制作「人类可读指纹」Feb 02, 2024 pm 09:33 PM将不同的基模型象征为不同品种的狗,其中相同的「狗形指纹」表明它们源自同一个基模型。大模型的预训练需要耗费大量的计算资源和数据,因此预训练模型的参数成为各大机构重点保护的核心竞争力和资产。然而,与传统软件知识产权保护不同,对预训练模型参数盗用的判断存在以下两个新问题:1)预训练模型的参数,尤其是千亿级别模型的参数,通常不会开源。预训练模型的输出和参数会受到后续处理步骤(如SFT、RLHF、continuepretraining等)的影响,这使得判断一个模型是否基于另一个现有模型微调得来变得困难。无
 FATE 2.0发布:实现异构联邦学习系统互联Jan 16, 2024 am 11:48 AM
FATE 2.0发布:实现异构联邦学习系统互联Jan 16, 2024 am 11:48 AMFATE2.0全面升级,推动隐私计算联邦学习规模化应用FATE开源平台宣布发布FATE2.0版本,作为全球领先的联邦学习工业级开源框架。此次更新实现了联邦异构系统之间的互联互通,持续增强了隐私计算平台的互联互通能力。这一进展进一步推动了联邦学习与隐私计算规模化应用的发展。FATE2.0以全面互通为设计理念,采用开源方式对应用层、调度、通信、异构计算(算法)四个层面进行改造,实现了系统与系统、系统与算法、算法与算法之间异构互通的能力。FATE2.0的设计兼容了北京金融科技产业联盟的《金融业隐私计算
 220亿晶体管,IBM机器学习专用处理器NorthPole,能效25倍提升Oct 23, 2023 pm 03:13 PM
220亿晶体管,IBM机器学习专用处理器NorthPole,能效25倍提升Oct 23, 2023 pm 03:13 PMIBM再度发力。随着AI系统的飞速发展,其能源需求也在不断增加。训练新系统需要大量的数据集和处理器时间,因此能耗极高。在某些情况下,执行一些训练好的系统,智能手机就能轻松胜任。但是,执行的次数太多,能耗也会增加。幸运的是,有很多方法可以降低后者的能耗。IBM和英特尔已经试验过模仿实际神经元行为设计的处理器。IBM还测试了在相变存储器中执行神经网络计算,以避免重复访问RAM。现在,IBM又推出了另一种方法。该公司的新型NorthPole处理器综合了上述方法的一些理念,并将其与一种非常精简的计算运行
 制作莫比乌斯环,最少需要多长纸带?50年来的谜题被解开了Oct 07, 2023 pm 06:17 PM
制作莫比乌斯环,最少需要多长纸带?50年来的谜题被解开了Oct 07, 2023 pm 06:17 PM自己动手做过莫比乌斯带吗?莫比乌斯带是一种奇特的数学结构。要构造一个这样美丽的单面曲面其实非常简单,即使是小孩子也可以轻松完成。你只需要取一张纸带,扭曲一次,然后将两端粘在一起。然而,这样容易制作的莫比乌斯带却有着复杂的性质,长期吸引着数学家们的兴趣。最近,研究人员一直被一个看似简单的问题困扰着,那就是关于制作莫比乌斯带所需纸带的最短长度?布朗大学RichardEvanSchwartz谈到,对于莫比乌斯带来说,这个问题没有解决,因为它们是「嵌入的」而不是「浸入的」,这意味着它们不会相互渗透或自我


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

SublimeText3 英文版
推薦:為Win版本,支援程式碼提示!

SublimeText3漢化版
中文版,非常好用

WebStorm Mac版
好用的JavaScript開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

SublimeText3 Linux新版
SublimeText3 Linux最新版





