神经网络作为深度学习技术的基础已经在诸多应用领域取得了有效成果。在实践中,网络架构可以显著影响学习效率,一个好的神经网络架构能够融入问题的先验知识,确立网络训练,提高计算效率。目前,经典的网络架构设计方法包括人工设计、神经网络架构搜索(NAS)[1]、以及基于优化的网络设计方法 [2]。人工设计的网络架构如 ResNet 等;神经网络架构搜索则通过搜索或强化学习的方式在搜索空间中寻找最佳网络结构;基于优化的设计方法中的一种主流范式是算法展开(algorithm unrolling),该方法通常在有显式目标函数的情况下,从优化算法的角度设计网络结构。 这些方法在优化算法的角度设计网络结构时,从优化算法的角度设计网络结构。
现今有经典神经网络架构设计大多忽略了网络的万有逼近性——这是神经网络具备强大性能的关键因素之一。因此,这些设计方法在一定程度上失去了网络的先验性能保障。尽管两层神经网络在宽度趋于无穷的时候已具有万有逼近性质 [3],在实际中,我们通常只能考虑有限宽度的网络结构,这方面的表现分析的结果十分有限。实际上,启发性的人工设计,还是黑匣性质的神经网络架构搜索,都很难在网络设计中考虑万有逼近性质。基于优化的神经网络设计虽然相对更具解释性,但其通常需要一个明显的目标函数,这使得设计的网络结构种类有限,限制了其应用范围。如何系统性地设计工具有万有逼近性质的神经网络架构,仍然是一个重要的问题。
北京大学林宙辰教授团队提出了一种基于优化算法设计工具的神经网络架构,该方法通过将基于梯度的一阶优化算法与基于哈希的二阶优化算法相结合,提高了训练速度和收敛性能,并且增强了神经网络的鲁棒性保障。该神经网络模块也可用于现有基于模块化的网络设计方法,并且不断提高了模型的表现。最近,他们通过分析神经网络微分方程(NODE)的逼近性质,证明了跨层连接的神经网络具有万有近似性质,并利用提出的框架设计了ConvNext、ViT等变种网络,取得了超越baseline的结果。该论文被人工智能顶刊TPAMI接收。

- 论文:Designing Universally-Approximating Deep Neural Networks: A First-Order Optimization Approach
- 论文地址:https://ieeexplore.ieee.org/document/10477580
方法简介
传统的基于优化的神经网络设计方法常常从一个具有显式表达式的目标函数出发,采用特定的优化算法进行求解,再将优化结果映射为神经网络结构,例如著名的 LISTA-NN 就是利用 LISTA 算法求解 LASSO 问题所得到的显式表达式,将优化结果转化为神经网络结构 [4]。这种方法对于目标函数的显式表达式有着很强的依赖性,因此所得到的网络结构只能针对目标函数的显式表达式进行优化,存在着设计出不符合实际情况的假设的风险。 一些研究者尝试通过自定义目标函数,再利用算法展开等方法设计网络结构,但他们也需要如权重重绑定等实际情况下不一定符合假设的假设。因此,一些研究者提出使用基于神经网络的进化算法进行网络架构搜索,来获取更加合理的网络结构。
网络架构设计方案的更新格式应遵循从一阶优化算法到更近点算法的思路,进行逐步优化。例如,可以将欧拉角算法改为四元数算法,或者采用更加高效的迭代算法来近似求解。更新格式应考虑增加计算精度和提高运行效率。

其中 、
、 表示第k 步更新時的(步長)係數,再將梯度項替換為神經網路中的可學習模組T,即可得到L 層神經網路的骨架:
表示第k 步更新時的(步長)係數,再將梯度項替換為神經網路中的可學習模組T,即可得到L 層神經網路的骨架:

整體方法框架見圖1。

圖1 網路設計圖示
論文提出的方法可以啟發設計ResNet、DenseNet 等經典網絡,並且解決了傳統基於最佳化設計網絡架構的方法局限於特定目標函數的問題。
模組選取與架構細節
#該方法所設計的網路模組T 只要求有包含兩層網絡結構,即 ,作為其子結構,即可保證所設計的網絡具有萬有逼近性質,其中所表達的層的寬度是有限的(即不隨逼近精度的提高而成長),整個網路的萬有逼近性質不是靠加寬
,作為其子結構,即可保證所設計的網絡具有萬有逼近性質,其中所表達的層的寬度是有限的(即不隨逼近精度的提高而成長),整個網路的萬有逼近性質不是靠加寬 的層來獲得的。模組 T 可以是 ResNet 中廣泛運用的 pre-activation 區塊,也可以是 Transformer 中的注意力 前饋層的結構。 T 中的激活函數可以是 ReLU、GeLU、Sigmoid 等常用激活函數。也可以根據具體任務在中加入對應的歸一化層。另外,當
的層來獲得的。模組 T 可以是 ResNet 中廣泛運用的 pre-activation 區塊,也可以是 Transformer 中的注意力 前饋層的結構。 T 中的激活函數可以是 ReLU、GeLU、Sigmoid 等常用激活函數。也可以根據具體任務在中加入對應的歸一化層。另外,當 時,設計的網路是隱式網路[5],可以用不動點迭代的方法逼近隱格式,或採用隱式微分(implicit differentiation)的方法來求解梯度進行更新。
時,設計的網路是隱式網路[5],可以用不動點迭代的方法逼近隱格式,或採用隱式微分(implicit differentiation)的方法來求解梯度進行更新。
透過等價表示設計更多網路
#該方法不要求同一種演算法只能對應一種結構,相反,該方法可以利用最佳化問題的等價表示設計更多的網路架構,體現其靈活性。例如,線性化交替方向乘子法通常用於求解約束最佳化問題: 透過令
透過令 即可得到一種可啟發網路的更新迭代格式:
即可得到一種可啟發網路的更新迭代格式:

其啟發的網路結構可見圖2。

圖2 線性化交替方向乘子法啟發的網路結構
啟發的網路具有萬有逼近性質
#對此方法設計的網路架構,可以證明,在模組滿足先前條件以及優化演算法(在一般情況下)穩定、收斂的條件下,任意一階優化演算法啟發的神經網路在高維連續函數空間具有萬有逼近性質,並給出了逼近速度。論文首次在有限寬度設定下證明了具有一般跨層連接的神經網路的萬有逼近性質(先前研究基本集中在FCNN 和ResNet,見表1),論文主定理可簡略敘述如下:
主定理(簡單版):設 # A 為梯度型一階最佳化演算法。若演算法A 具有公式(1) 中的更新格式,且滿足收斂性條件(最佳化演算法的常用步長選取均符合收斂性條件。若在啟發網路中均為可學習的,則可以不需要該條件) ,則由演算法啟發的神經網路:
# A 為梯度型一階最佳化演算法。若演算法A 具有公式(1) 中的更新格式,且滿足收斂性條件(最佳化演算法的常用步長選取均符合收斂性條件。若在啟發網路中均為可學習的,則可以不需要該條件) ,則由演算法啟發的神經網路:

在連續(向量值)函數空間 #以及範數
#以及範數 下具有萬有逼近性質,其中可學習模組T 只要有包含兩層形如
下具有萬有逼近性質,其中可學習模組T 只要有包含兩層形如 的結構(σ 可以是常用的激活函數)作為其子結構都可以。
的結構(σ 可以是常用的激活函數)作為其子結構都可以。
常用的T 的結構如:
1)卷積網路中,pre-activation 區塊:BN-ReLU-Conv-BN -ReLU-Conv (z),
2)Transformer 中:Attn (z) MLP (z Attn (z)).
主定理的證明利用了NODE 的萬有逼近性質以及線性多步方法的收斂性質,核心是證明優化演算法啟發設計的網絡結構恰對應一種收斂的線性多步方法對連續的NODE 的離散化,從而啟發的網路「繼承」 了NODE 的逼近能力。在證明中,論文還給出了 NODE 逼近 d 維空間連續函數的逼近速度,解決了先前論文 [6] 的一個遺留問題。

表1 先前萬有逼近性質的研究基本上集中在FCNN 和ResNet
##實驗結果
論文利用所提出的網路架構設計框架設計了8 種明確網路和3 種隱式網路(稱為OptDNN),網路資訊見表2,並在嵌套環分離、函數逼近和影像分類等問題上進行了實驗。論文也以 ResNet, DenseNet, ConvNext 以及 ViT 為 baseline,利用所提出的方法設計了改進的 OptDNN,並在圖像分類的問題上進行實驗,考慮準確率和 FLOPs 兩個指標。

表2 所設計網路的資訊
首先,OptDNN 在巢狀環分離和函數逼近兩個問題上進行實驗,以驗證其萬有逼近性質。在函數逼近問題中,分別考慮了逼近 parity function 和 Talgarsky function,前者可表示為二分類問題,後者則是迴歸問題,這兩個問題都是淺層網路難以逼近的問題。 OptDNN 在嵌套環分離的實驗結果如圖3 所示,在函數逼近的實驗結果如圖3 所示,OptDNN 不僅取得了很好的分離/ 逼近結果,而且比作為baseline 的ResNet 取得了更大的分類間隔和更小的迴歸誤差,足以驗證OptDNN 的萬有逼近性質。

圖3 OptNN 逼近parity function

圖4 OptNN 逼近Talgarsky function
然後,OptDNN 分別在寬- 淺和窄- 深兩種設定下在CIFAR 數據集上進行了圖像分類任務的實驗,結果見表3 與4。實驗均在較強的資料增強設定下進行,可以看出,一些 OptDNN 在相同甚至更小的 FLOPs 開銷下取得了比 ResNet 更小的錯誤率。論文也在 ResNet 和 DenseNet 設定下進行了實驗,也取得了類似的實驗結果。

表3 OptDNN 在寬- 淺設定下的實驗結果

表4 OptDNN 在窄- 深設定下的實驗結果
論文進一步選取了先前表現較好的OptDNN-APG2 網絡,進一步在ConvNext 和ViT 的設定下在ImageNet 資料集上進行了實驗,OptDNN-APG2 的網路結構見圖5,實驗結果表5、6。 OptDNN-APG2 取得了超過等寬 ConvNext、ViT 的準確率,進一步驗證了此架構設計方法的可靠性。

圖5 OptDNN-APG2 的網路結構

表5 OptDNN-APG2 在ImageNet 上的效能比較

表6 OptDNN-APG2 與等寬(isotropic)的ConvNeXt 和ViT 的效能比較
最後,論文依照Proximal Gradient Descent 和FISTA 等演算法設計了3 個隱式網絡,並在CIFAR 資料集上和明確的ResNet 以及一些常用的隱式網絡進行了比較,實驗結果如表7。三個隱式網路都取得了與先進隱式網路相當的實驗結果,也說明了方法的靈活性。

表7 隱式網路的效能比較
總結
#神經網路架構設計是深度學習中的核心問題之一。論文提出了一個利用一階最佳化演算法設計具有萬有逼近性質保障的神經網路架構的統一框架,拓展了基於最佳化設計網路架構範式的方法。此方法可與現有大部分聚焦網路模組的架構設計方法結合,可以在幾乎不增加運算量的情況下設計出高效的模型。在理論方面,論文證明了收斂的最佳化演算法誘導的網路架構在溫和條件下即具有萬有逼近性質,並彌合了 NODE 和具有一般跨層連接網路的表示能力。該方法還有望與 NAS、 SNN 架構設計等領域結合,以設計更有效率的網路架構。
以上是一階最佳化演算法啟發,北大林宙辰團隊提出具有萬有逼近性質的神經網路架構的設計方法的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM
讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM科學家已經廣泛研究了人類和更簡單的神經網絡(如秀麗隱桿線蟲中的神經網絡),以了解其功能。 但是,出現了一個關鍵問題:我們如何使自己的神經網絡與新穎的AI一起有效地工作
 新的Google洩漏揭示了雙子AI的訂閱更改Apr 27, 2025 am 11:08 AM
新的Google洩漏揭示了雙子AI的訂閱更改Apr 27, 2025 am 11:08 AMGoogle的雙子座高級:新的訂閱層即將到來 目前,訪問Gemini Advanced需要$ 19.99/月Google One AI高級計劃。 但是,Android Authority報告暗示了即將發生的變化。 最新的Google P中的代碼
 數據分析加速度如何求解AI的隱藏瓶頸Apr 27, 2025 am 11:07 AM
數據分析加速度如何求解AI的隱藏瓶頸Apr 27, 2025 am 11:07 AM儘管圍繞高級AI功能炒作,但企業AI部署中潛伏的巨大挑戰:數據處理瓶頸。首席執行官慶祝AI的進步時,工程師努力應對緩慢的查詢時間,管道超載,一個
 Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM
Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM處理文檔不再只是在您的AI項目中打開文件,而是將混亂變成清晰度。諸如PDF,PowerPoints和Word之類的文檔以各種形狀和大小淹沒了我們的工作流程。檢索結構化
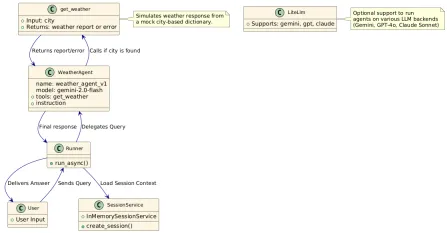 如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM
如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM利用Google的代理開發套件(ADK)的力量創建具有現實世界功能的智能代理!該教程通過使用ADK來構建對話代理,並支持Gemini和GPT等各種語言模型。 w
 在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM
在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM摘要: 小型語言模型 (SLM) 專為效率而設計。在資源匱乏、實時性和隱私敏感的環境中,它們比大型語言模型 (LLM) 更勝一籌。 最適合專注型任務,尤其是在領域特異性、控制性和可解釋性比通用知識或創造力更重要的情況下。 SLM 並非 LLMs 的替代品,但在精度、速度和成本效益至關重要時,它們是理想之選。 技術幫助我們用更少的資源取得更多成就。它一直是推動者,而非驅動者。從蒸汽機時代到互聯網泡沫時期,技術的威力在於它幫助我們解決問題的程度。人工智能 (AI) 以及最近的生成式 AI 也不例
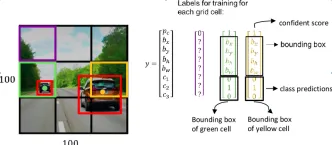 如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM
如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM利用Google雙子座的力量用於計算機視覺:綜合指南 領先的AI聊天機器人Google Gemini擴展了其功能,超越了對話,以涵蓋強大的計算機視覺功能。 本指南詳細說明瞭如何利用
 Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM2025年的AI景觀正在充滿活力,而Google的Gemini 2.0 Flash和Openai的O4-Mini的到來。 這些尖端的車型分開了幾週,具有可比的高級功能和令人印象深刻的基準分數。這個深入的比較


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

PhpStorm Mac 版本
最新(2018.2.1 )專業的PHP整合開發工具

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

MantisBT
Mantis是一個易於部署的基於Web的缺陷追蹤工具,用於幫助產品缺陷追蹤。它需要PHP、MySQL和一個Web伺服器。請查看我們的演示和託管服務。

Dreamweaver CS6
視覺化網頁開發工具






