機器學習中七種常用的線性降維技術總結

上篇文章中我們主要總結了非線性的降維技術，本文我們來總結常見的線性降維技術。

1、Principal Component Analysis (PCA)

PCA是一種廣泛應用的降維技術，可以將高維度資料集轉換為更易處理的低維表示，同時保留資料的關鍵特徵。透過辨識資料中方差最大的方向（主成分），PCA能夠將資料投影到這些方向上，實現降維的目標。

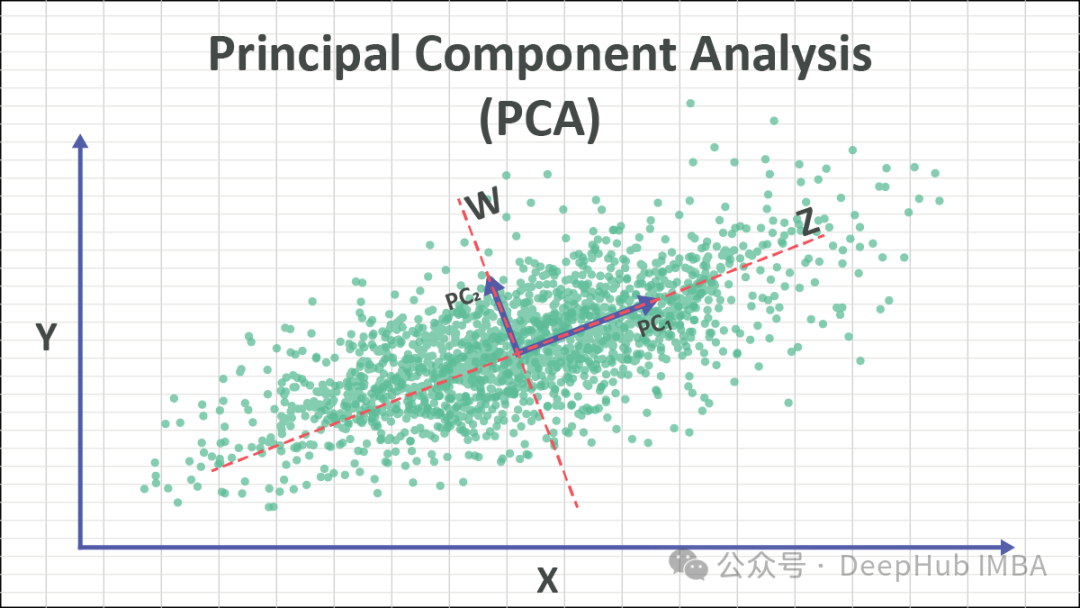
PCA的核心思想是將原始資料轉換到一個新的座標系，以最大化資料的變異數。這些新座標軸稱為主成分，由原始特徵線性組合而成。保留方差最大的主成分，實質上保留了資料的關鍵資訊。透過捨棄方差較小的主成分，可以實現降維的目的。

PCA 的步驟如下：

1. 標準化資料：將原始資料標準化處理，使得每個特徵的平均值為 0，變異數為 1。
2. 計算協方差矩陣：計算標準化後的資料的協方差矩陣。
3. 計算特徵值和特徵向量：對協方差矩陣進行特徵值分解，得到特徵值和對應的特徵向量。
4. 選擇主成分：依照特徵值的大小選擇前 k 個特徵向量作為主成分，其中 k 是降維後的維度。
5. 投影資料：將原始資料投影到選定的主成分上，得到降維後的資料集。

PCA可以用於資料降維、特徵提取和模式識別等任務。在使用PCA時，需要確保資料符合線性可分的基本假設，並進行必要的資料預處理和理解，以獲得準確的降維效果。

2、Factor Analysis (FA)

Factor Analysis (FA) is a statistical technique used to identify the underlying structure or factors among observed variables. It aims to uncover the latent factors that account for the shared variance among the observed variables, ultimately reducing them to a smaller number of unrelated variables.

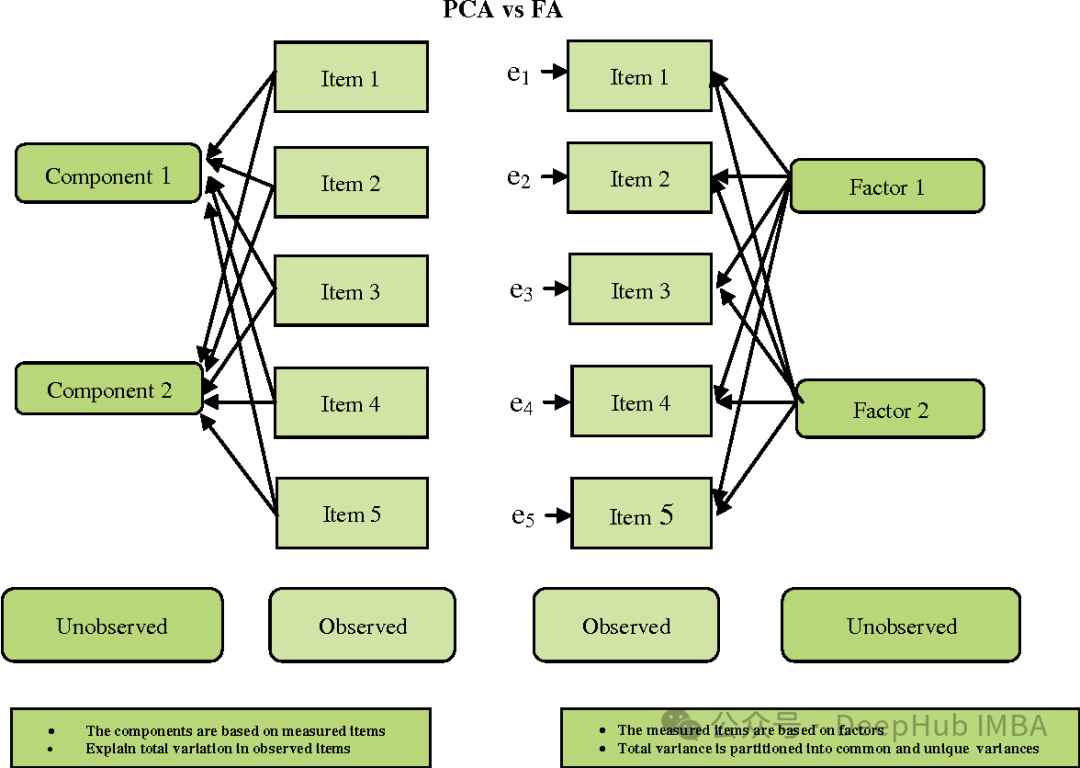
FA 和PCA 有些相似，但也有一些重要的區別：

1. #FA 和PCA 有些相似，但也有一些重要的區別：
3. #FA 和PCA 有些相似，但也有一些重要的區別：

#FA 和PCA 有些相似，但也有一些重要的區別：

目標：PCA 旨在找到最大變異數的方向，而F​​A 旨在找到潛在的變數(因素)，這些變數能夠解釋觀察到的變數之間的共同變異。

假設：PCA 假設觀察到的變數是觀察到的原始特徵，而 FA 假設觀察到的變數是潛在因素的線性組合和隨機誤差的總和。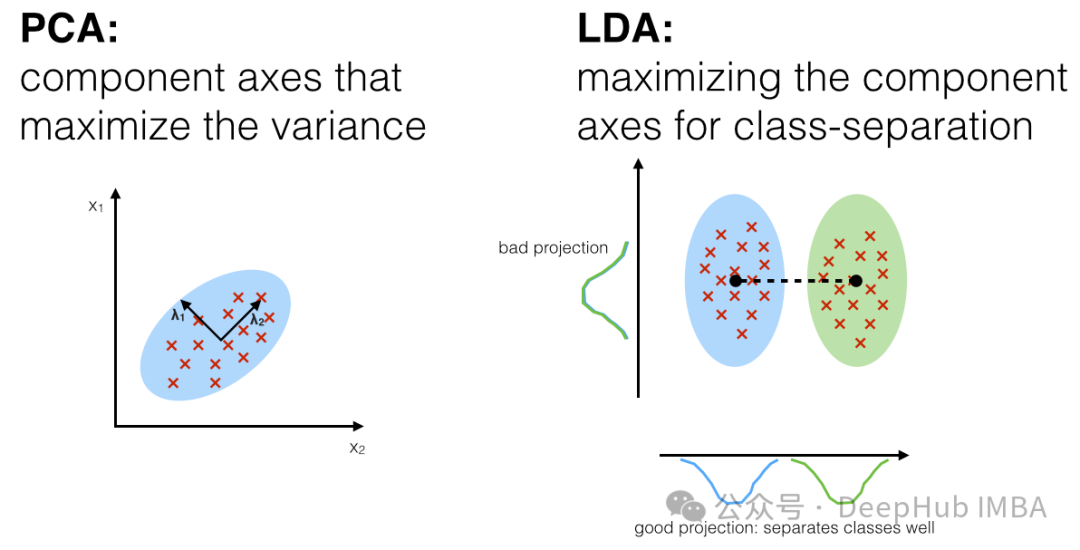

解釋性：PCA 往往更直接，因為它的主成分是原始特徵的線性組合。而 FA 的因素可能不太容易解釋，因為它們是觀察到的變數的線性組合，而非原始特徵。

旋轉：在 FA 中，因素通常會進行旋轉，以使它們更易於解釋。

######因子分析在心理學、社會科學和市場研究等領域廣泛應用。它有助於簡化資料集、發現潛在結構和減少測量誤差。但在選擇因子數量和旋轉方法時需慎重，以確保結果可解釋且有效。 ######3、Linear Discriminant Analysis，LDA######線性判別分析(Linear Discriminant Analysis，LDA)是一種用於降維和特徵提取的監督學習技術。它與主成分分析(PCA)不同，因為它不僅考慮了資料的變異數結構，還考慮了資料的類別資訊。 LDA 旨在找到一個投影方向，最大化不同類別之間的距離(類間散佈)，同時最小化同一類別內部的距離(類內散佈)。 ###############LDA 的主要步驟如下：###

1. 計算類別的平均值向量：對於每個類別，計算該類別下所有樣本的平均值向量。
2. 計算類別內散佈矩陣(Within-class scatter matrix)：對於每個類別，計算該類別下所有樣本與其平均值向量之間的散佈矩陣，並將它們求和。
3. 計算類間散佈矩陣(Between-class scatter matrix)：計算所有類別的平均值向量與總體平均值向量之間的散佈矩陣。
4. 計算特徵值和特徵向量：對於矩陣的逆矩陣乘以類間散佈矩陣，得到的矩陣進行特徵值分解，得到特徵值和特徵向量。
5. 選擇投影方向：選擇特徵值最大的前 k 個特徵向量作為投影方向，其中 k 是降維後的維度。
6. 投影資料：將原始資料投影到選定的投影方向上，得到降維後的資料。

LDA 的優點在於它考慮了資料的類別訊息，因此產生的投影能更好地區分不同類別之間的差異。它在模式識別、人臉辨識、語音辨識等領域中有著廣泛的應用。 LDA 在處理多類別和類別不平衡的情況下可能會遇到一些問題，需要特別注意。

4、Eigendecomposition

Eigendecomposition(特徵值分解)是一種用於對方陣進行分解的數學技術。它將一個方陣分解為一組特徵向量和特徵值的乘積形式。特徵向量表示了在轉換中不改變方向的方向，而特徵值表示了在轉換中沿著這些方向的縮放比例。

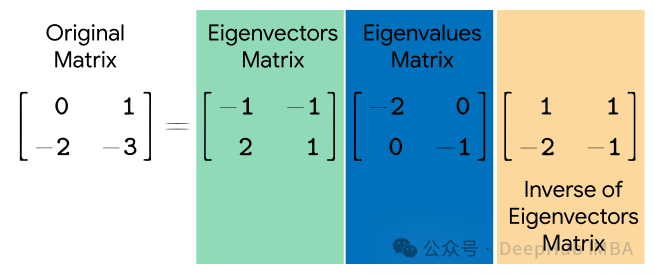
給定方陣AA，其特徵值分解表示為：

其中，Q是由A的特徵向量所組成的矩陣，Λ是對角矩陣，其對角線上的元素是A的特徵值。

特徵值分解有許多應用，包括主成分分析(PCA)、特徵臉辨識、譜聚類等。在PCA中，特徵值分解用於找到資料協方差矩陣的特徵向量，從而找到資料的主成分。在譜聚類中，特徵值分解用於找到相似性圖的特徵向量，從而進行聚類。特徵臉辨識利用了特徵值分解來辨識人臉影像中的重要特徵。

雖然特徵值分解在許多應用中非常有用，但並非所有的方陣都能進行特徵值分解。例如，奇異矩陣(singular matrix)或非方陣就不能進行特徵值分解。特徵值分解在大型矩陣計算上可能是非常耗時的。

5、Singular value decomposition (SVD)

奇異值分解(Singular Value Decomposition，SVD)是一種用於矩陣分解的重要技術。它將一個矩陣分解為三個矩陣的乘積形式，這三個矩陣分別是一個正交矩陣、一個對角矩陣和另一個正交矩陣的轉置。

給定一個m × n 的矩陣AA，其奇異值分解表示為：

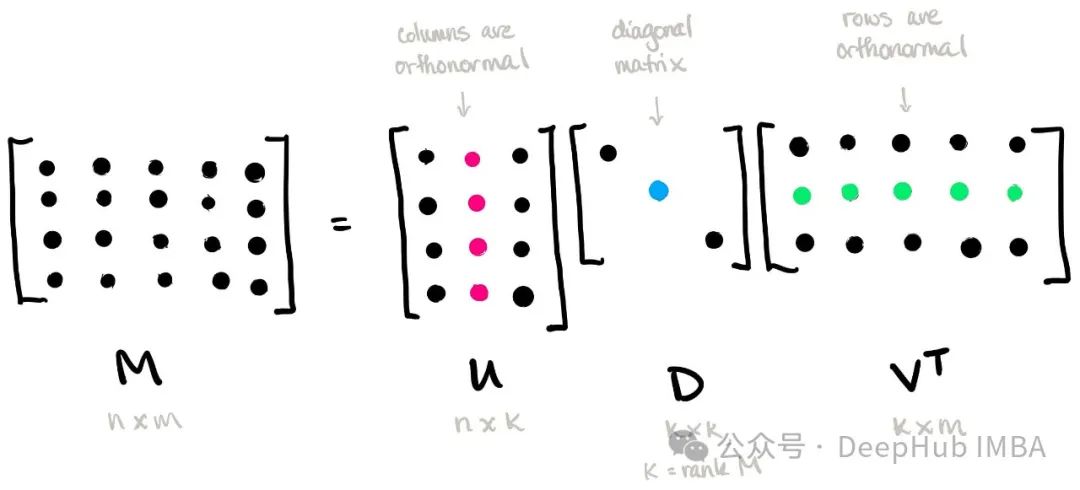
其中，U 是一個m × m 的正交矩陣，稱為左奇異向量矩陣;Σ 是一個m × n 的對角矩陣，其對角線上的元素稱為奇異值;VT 是一個n × n 的正交矩陣的轉置，稱為右奇異向量矩陣。

奇異值分解有廣泛的應用，包括資料壓縮、降維、矩陣逆求解、推薦系統等。在降維中，只保留奇異值較大的項，可以實現對資料的有效壓縮和表示。在推薦系統中，透過奇異值分解可以對使用者和項目之間的關係進行建模，從而提供個人化的推薦。

奇異值分解也可以用於矩陣逆求解，特別是對於奇異矩陣。保留奇異值較大的項，可以近似求解逆矩陣，從而避免了對奇異矩陣求逆的問題。

6、Truncated Singular Value Decomposition (TSVD)

截斷奇異值分解(Truncated Singular Value Decomposition，TSVD)是奇異值分解(SVD)的變體，它在計算中只保留最重要的奇異值和對應的奇異向量，從而實現資料的降維和壓縮。

給定一個m × n 的矩陣AA，其截斷奇異值分解表示為：

其中，Uk 是m × k 的正交矩陣，Σk 是一個k × k 的對角矩陣，VkT 是一個k × n 的正交矩陣的轉置，這些矩陣對應於保留最重要的k 個奇異值和對應的奇異向量。

TSVD 的主要优点在于它可以通过保留最重要的奇异值和奇异向量来实现数据的降维和压缩，从而减少了存储和计算成本。这在处理大规模数据集时尤其有用，因为可以显著减少所需的存储空间和计算时间。

TSVD 在许多领域都有应用，包括图像处理、信号处理、推荐系统等。在这些应用中，TSVD 可以用于降低数据的维度、去除噪声、提取关键特征等。

7、Non-Negative Matrix Factorization (NMF)

Non-Negative Matrix Factorization (NMF) 是一种用于数据分解和降维的技术，其特点是分解得到的矩阵和向量都是非负的。这使得 NMF 在许多应用中都很有用，特别是在文本挖掘、图像处理和推荐系统等领域。

给定一个非负矩阵 VV，NMF 将其分解为两个非负矩阵 WW 和 HH 的乘积形式：

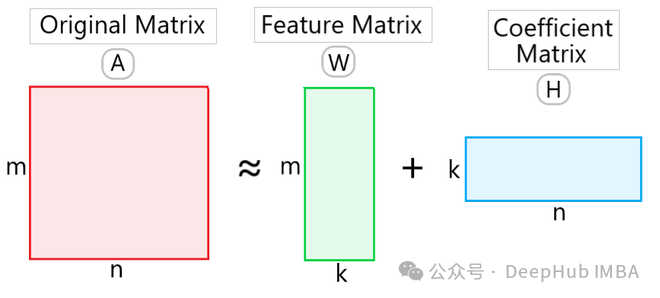
其中，W 是一个 m × k 的非负矩阵，称为基矩阵(basis matrix)或者特征矩阵(feature matrix)，H 是一个 k × n 的非负矩阵，称为系数矩阵(coefficient matrix)。这里的 k 是降维后的维度。

NMF 的优点在于它能够得到具有物理含义的分解结果，因为所有的元素都是非负的。这使得 NMF 在文本挖掘中能够发现潜在的主题，而在图像处理中能够提取出图像的特征。此外，NMF 还具有数据降维的功能，可以减少数据的维度和存储空间。

NMF 的应用包括文本主题建模、图像分割与压缩、音频信号处理、推荐系统等。在这些领域中，NMF 被广泛应用于数据分析和特征提取，以及信息检索和分类等任务中。

总结

线性降维技术是一类用于将高维数据集映射到低维空间的技术，其核心思想是通过线性变换来保留数据集的主要特征。这些线性降维技术在不同的应用场景中有其独特的优势和适用性，可以根据数据的性质和任务的要求选择合适的方法。例如，PCA适用于无监督的数据降维，而LDA适用于监督学习任务。

结合前一篇文章，我们介绍了10种非线性降维技术核7种线性降维技术，下面我们来做个总结

线性降维技术：基于线性变换将数据映射到低维空间，适用于线性可分的数据集;例如数据点分布在一个线性子空间上的情况;因为其算法简单，所以计算效率高，易于理解和实现;通常不能捕捉数据中的非线性结构，可能会导致信息丢失。

非线性降维技术：通过非线性变换将数据映射到低维空间;适用于非线性结构的数据集，例如数据点分布在流形上的情况;能够更好地保留数据中的非线性结构和局部关系，提供更好的可视化效果;计算复杂度较高，通常需要更多的计算资源和时间。

如果数据是线性可分的或者计算资源有限，可以选择线性降维技术。而如果数据包含复杂的非线性结构或者需要更好的可视化效果，可以考虑使用非线性降维技术。在实践中，也可以尝试不同的方法，并根据实际效果来选择最合适的降维技术。

以上是機器學習中七種常用的線性降維技術總結的詳細內容。更多資訊請關注PHP中文網其他相關文章！