機器學習中的十種非線性降維技術比較總結

降維是指在減少資料集特徵數量的同時，盡可能保留資料的主要資訊。降維演算法屬於無監督學習，透過未標記資料來訓練演算法。

儘管降維方法種類繁多，但它們都可以歸為兩大類:線性和非線性。

線性方法將資料從高維空間線性投影到低維空間(因此稱為線性投影)。例子包括PCA和LDA。

非線性方法是執行非線性降維的一種途徑，通常用於發現原始資料的非線性結構。當原始資料不容易線性分離時，非線性降維方法就顯得特別重要。在某些情況下，非線性降維也被稱為流形學習，這種方法能夠更有效地處理高維度數據，並幫助揭示數據的潛在結構。透過非線性降維，我們可以更好地理解數據之間的關係，發現數據中隱藏的模式和規律，為進一步的數據分析和應用提供有力支持。

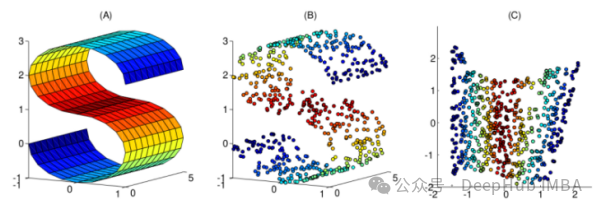
本文整理了10個常用的非線性降維技術，可以幫助你在日常工作中進行選擇

1、核PCA

#你們可能熟悉正常的PCA，這是一種線性降維技術。核PCA可以看作是常態主成分分析的非線性版本。

主成分分析和核主成分分析都可用於降維，但核PCA在處理線性不可分資料方面更為有效。核PCA的主要優勢在於將非線性可分的資料轉換為線性可分，同時減少資料維度。核PCA透過引入核技巧，能夠捕捉資料中的非線性結構，從而提高資料的分類性能。因此，核PCA在處理複雜資料集時具有更強的表現力和泛化能力。

我們先建立一個非常經典的資料：

import matplotlib.pyplot as plt plt.figure(figsize=[7, 5])  from sklearn.datasets import make_moons X, y = make_moons(n_samples=100, noise=None, random_state=0)  plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='plasma') plt.title('Linearly inseparable data')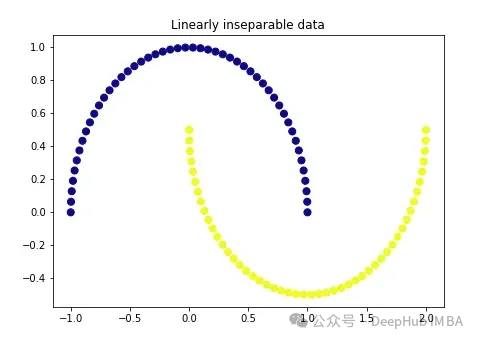

#這兩個顏色代表線性上不可分割的兩個類別。我們不可能在這裡畫一條直線把這兩類分開。

我們先使用常規PCA。

 import numpy as np from sklearn.decomposition import PCA  pca = PCA(n_components=1) X_pca = pca.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_pca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after linear PCA') plt.xlabel('PC1')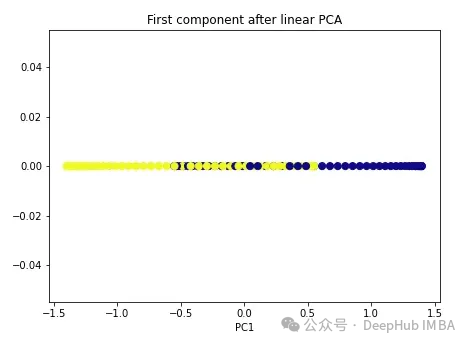

可以看到，這兩個類別仍然是線性不可分割的，現在我們試試看核PCA。

 import numpy as np from sklearn.decomposition import KernelPCA  kpca = KernelPCA(n_components=1, kernel='rbf', gamma=15) X_kpca = kpca.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_kpca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.axvline(x=0.0, linestyle='dashed', color='black', linewidth=1.2) plt.title('First component after kernel PCA') plt.xlabel('PC1')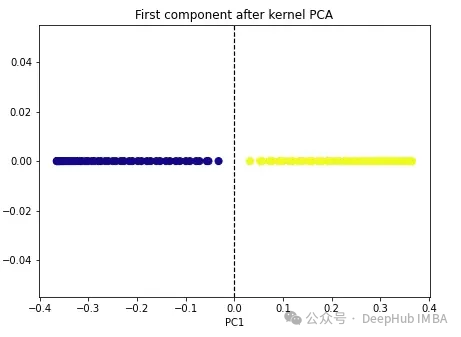

這兩個類別變成了線性可分的，核PCA演算法使用不同的核將資料從一種形式轉換為另一種形式。核PCA是一個兩步驟的過程。首先核函數暫時將原始資料投影到高維空間中，在高維空間中，類別是線性可分的。然後演算法將該資料投影回n_components超參數(我們想要保留的維數)中指定的較低維度。

sklearn中有四個核選項:linear’, ‘poly’, ‘rbf’ and ‘sigmoid’。如果我們將核指定為“線性”，則將執行正常的PCA。任何其他核將執行非線性PCA。 rbf(徑向基底函數)核是最常用的。

2、多維尺度變換(multidimensional scaling, MDS)

多維尺度變換是另一種非線性降維技術，它透過保持高維度和低維度資料點之間的距離來執行降維。例如，原始維度中距離較近的點在低維形式中也顯得較近。

要在Scikit-learn我們可以使用MDS()類別。

 from sklearn.manifold import MDS  mds = MDS(n_components, metric) mds_transformed = mds.fit_transform(X)

metric 超參數區分了兩種類型的MDS演算法:metric和non-metric。如果metric=True，則執行metric MDS。否則，執行non-metric MDS。

我們將兩種類型的MDS演算法應用於以下非線性資料。

 import numpy as np from sklearn.manifold import MDS  mds = MDS(n_components=1, metric=True) # Metric MDS X_mds = mds.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('Metric MDS') plt.xlabel('Component 1')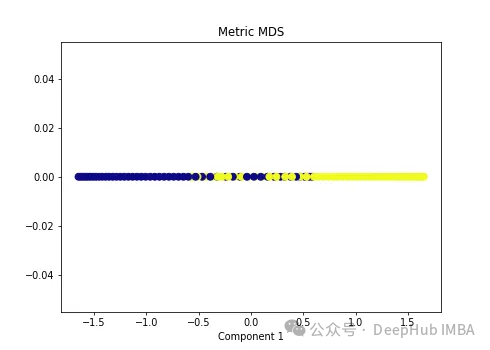

 import numpy as np from sklearn.manifold import MDS  mds = MDS(n_components=1, metric=False) # Non-metric MDS X_mds = mds.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('Non-metric MDS') plt.xlabel('Component 1')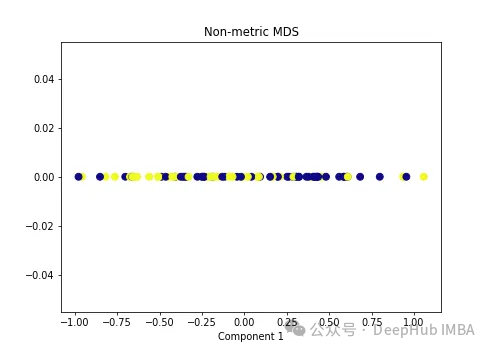

可以看到MDS后都不能使数据线性可分，所以可以说MDS不适合我们这个经典的数据集。

3、Isomap

Isomap(Isometric Mapping)在保持数据点之间的地理距离，即在原始高维空间中的测地线距离或者近似的测地线距离，在低维空间中也被保持。Isomap的基本思想是通过在高维空间中计算数据点之间的测地线距离(通过最短路径算法，比如Dijkstra算法)，然后在低维空间中保持这些距离来进行降维。在这个过程中，Isomap利用了流形假设，即假设高维数据分布在一个低维流形上。因此，Isomap通常在处理非线性数据集时表现良好，尤其是当数据集包含曲线和流形结构时。

 import matplotlib.pyplot as plt plt.figure(figsize=[7, 5])  from sklearn.datasets import make_moons X, y = make_moons(n_samples=100, noise=None, random_state=0)  import numpy as np from sklearn.manifold import Isomap  isomap = Isomap(n_neighbors=5, n_components=1) X_isomap = isomap.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_isomap[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying Isomap') plt.xlabel('Component 1')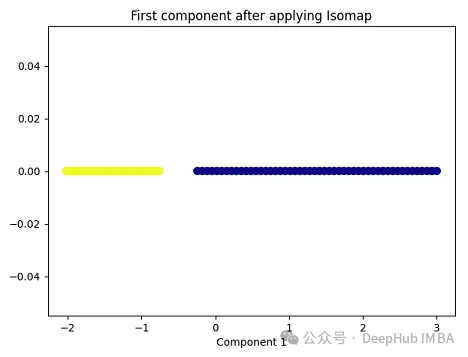

就像核PCA一样，这两个类在应用Isomap后是线性可分的!

4、Locally Linear Embedding(LLE)

与Isomap类似，LLE也是基于流形假设，即假设高维数据分布在一个低维流形上。LLE的主要思想是在局部邻域内保持数据点之间的线性关系，并在低维空间中重构这些关系。

 from sklearn.manifold import LocallyLinearEmbedding lle = LocallyLinearEmbedding(n_neighbors=5,n_components=1) lle_transformed = lle.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(lle_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying LocallyLinearEmbedding') plt.xlabel('Component 1')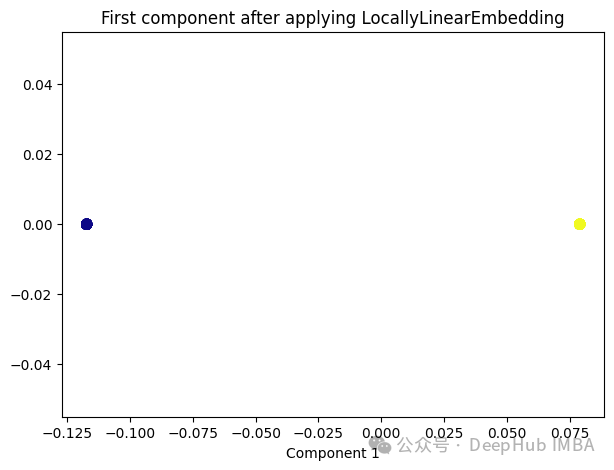

只有2个点，其实并不是这样，我们打印下这个数据

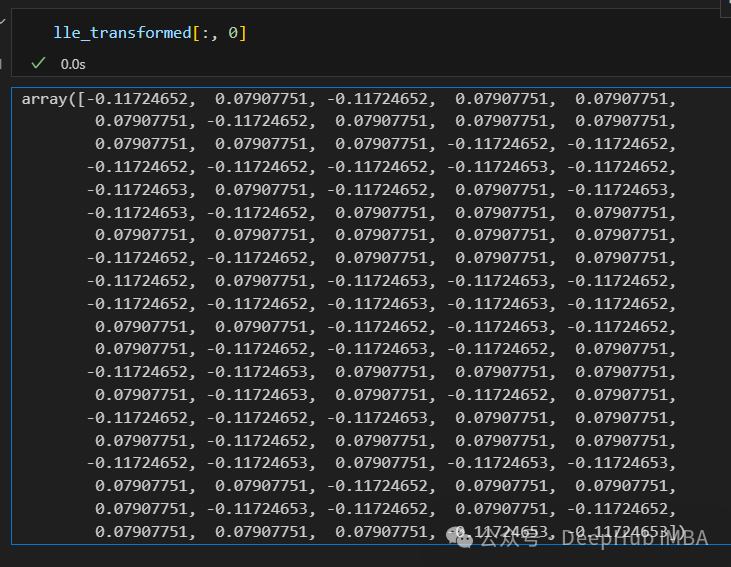
可以看到数据通过降维变成了同一个数字，所以LLE降维后是线性可分的，但是却丢失了数据的信息。

5、Spectral Embedding

Spectral Embedding是一种基于图论和谱理论的降维技术，通常用于将高维数据映射到低维空间。它的核心思想是利用数据的相似性结构，将数据点表示为图的节点，并通过图的谱分解来获取低维表示。

 from sklearn.manifold import SpectralEmbedding sp_emb = SpectralEmbedding(n_components=1, affinity='nearest_neighbors') sp_emb_transformed = sp_emb.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(sp_emb_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying SpectralEmbedding') plt.xlabel('Component 1')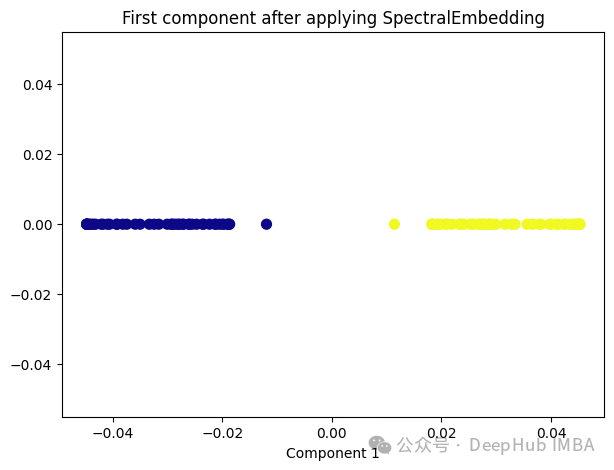

6、t-Distributed Stochastic Neighbor Embedding (t-SNE)

t-SNE的主要目标是保持数据点之间的局部相似性关系，并在低维空间中保持这些关系，同时试图保持全局结构。

from sklearn.manifold import TSNE tsne = TSNE(1, learning_rate='auto', init='pca') tsne_transformed = tsne.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(tsne_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying TSNE') plt.xlabel('Component 1')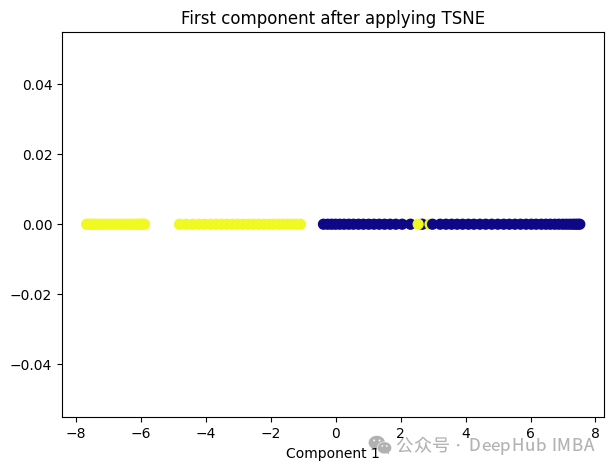

t-SNE好像也不太适合我们的数据。

7、Random Trees Embedding

Random Trees Embedding是一种基于树的降维技术，常用于将高维数据映射到低维空间。它利用了随机森林(Random Forest)的思想，通过构建多棵随机决策树来实现降维。

Random Trees Embedding的基本工作流程：

• 构建随机决策树集合：首先，构建多棵随机决策树。每棵树都是通过从原始数据中随机选择子集进行训练的，这样可以减少过拟合，提高泛化能力。
• 提取特征表示：对于每个数据点，通过将其在每棵树上的叶子节点的索引作为特征，构建一个特征向量。每个叶子节点都代表了数据点在树的某个分支上的位置。
• 降维：通过随机森林中所有树生成的特征向量，将数据点映射到低维空间中。通常使用降维技术，如主成分分析(PCA)或t-SNE等，来实现最终的降维过程。

Random Trees Embedding的优势在于它的计算效率高，特别是对于大规模数据集。由于使用了随机森林的思想，它能够很好地处理高维数据，并且不需要太多的调参过程。

RandomTreesEmbedding使用高维稀疏进行无监督转换，也就是说，我们最终得到的数据并不是一个连续的数值，而是稀疏的表示。所以这里就不进行代码展示了，有兴趣的看看sklearn的sklearn.ensemble.RandomTreesEmbedding

8、Dictionary Learning

Dictionary Learning是一种用于降维和特征提取的技术，它主要用于处理高维数据。它的目标是学习一个字典，该字典由一组原子(或基向量)组成，这些原子是数据的线性组合。通过学习这样的字典，可以将高维数据表示为一个更紧凑的低维空间中的稀疏线性组合。

Dictionary Learning的优点之一是它能够学习出具有可解释性的原子，这些原子可以提供关于数据结构和特征的重要见解。此外，Dictionary Learning还可以产生稀疏表示，从而提供更紧凑的数据表示，有助于降低存储成本和计算复杂度。

 from sklearn.decomposition import DictionaryLearning  dict_lr = DictionaryLearning(n_components=1) dict_lr_transformed = dict_lr.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(dict_lr_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying DictionaryLearning') plt.xlabel('Component 1')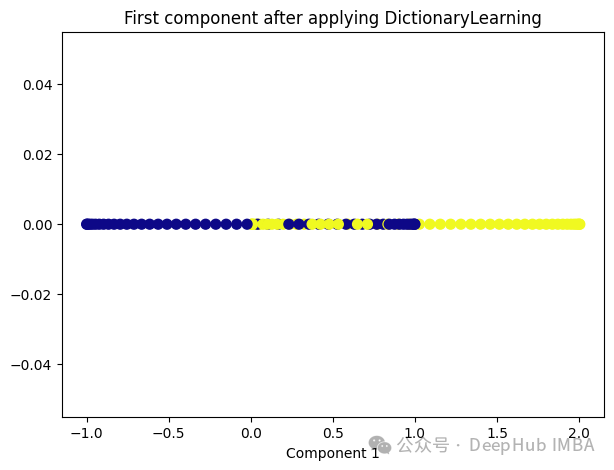

9、Independent Component Analysis (ICA)

Independent Component Analysis (ICA) 是一种用于盲源分离的统计方法，通常用于从混合信号中估计原始信号。在机器学习和信号处理领域，ICA经常用于解决以下问题：

• 盲源分离：给定一组混合信号，其中每个信号是一组原始信号的线性组合，ICA的目标是从混合信号中分离出原始信号，而不需要事先知道混合过程的具体细节。
• 特征提取：ICA可以被用来发现数据中的独立成分，提取数据的潜在结构和特征，通常在降维或预处理过程中使用。

ICA的基本假设是，混合信号中的各个成分是相互独立的，即它们的统计特性是独立的。这与主成分分析(PCA)不同，PCA假设成分之间是正交的，而不是独立的。因此ICA通常比PCA更适用于发现非高斯分布的独立成分。

 from sklearn.decomposition import FastICA  ica = FastICA(n_components=1, whiten='unit-variance') ica_transformed = dict_lr.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(ica_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying FastICA') plt.xlabel('Component 1')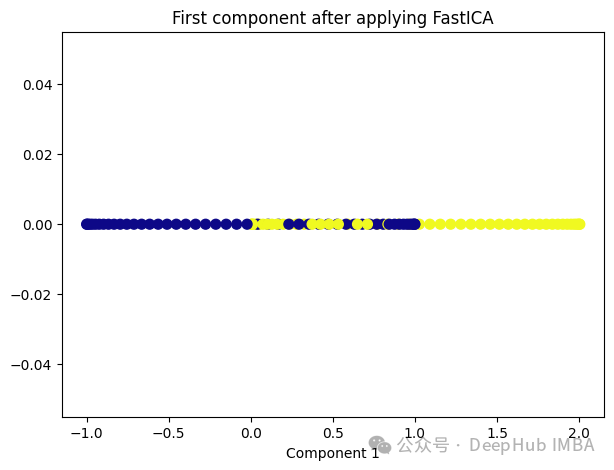

10、Autoencoders (AEs)

到目前为止，我们讨论的NLDR技术属于通用机器学习算法的范畴。而自编码器是一种基于神经网络的NLDR技术，可以很好地处理大型非线性数据。当数据集较小时，自动编码器的效果可能不是很好。

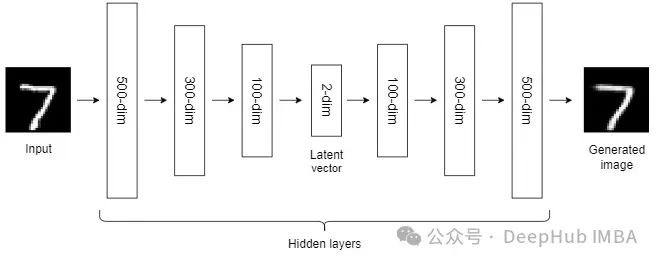
自编码器我们已经介绍过很多次了，所以这里就不详细说明了。

总结

非线性降维技术是一类用于将高维数据映射到低维空间的方法，它们通常适用于数据具有非线性结构的情况。

大多数NLDR方法基于最近邻方法，该方法要求数据中所有特征的尺度相同，所以如果特征的尺度不同，还需要进行缩放。

另外这些非线性降维技术在不同的数据集和任务中可能表现出不同的性能，因此在选择合适的方法时需要考虑数据的特征、降维的目标以及计算资源等因素。

以上是機器學習中的十種非線性降維技術比較總結的詳細內容。更多資訊請關注PHP中文網其他相關文章！