ICLR 2024 | 首個零階優化深度學習框架，MSU聯合LLNL提出DeepZero

本文是一篇關於提高零階最佳化的擴展性的研究，程式碼已開源，論文已被 ICLR 2024 接收。

今天我要介紹一篇題為「DeepZero: Scaling up Zeroth-Order Optimization for Deep Model Training」的論文，它由密西根州立大學和勞倫斯·利弗莫爾國家實驗室合作完成。這篇論文最近被ICLR 2024會議接收，研究團隊已經將程式碼開源。 該論文的主要目標是在深度學習模型訓練中擴展零階最佳化技術。零階優化是一種不依賴梯度資訊的最佳化方法，它可以更好地處理高維參數空間和複雜的模型結構。然而，現有的零階最佳化方法在處理深度學習模型時面臨規模和效率的挑戰。 為了解決這些挑戰，研究團隊提出了DeepZero框架。該框架透過引入新的採樣策略和自適應調整機制，能夠有效率地處理大規模深度學習模型的訓練。 DeepZero利用了零階最佳化的優勢，並結合了分散式運算和平行化技術，以加速訓練過

論文網址：https://arxiv.org/abs/2310.02025

• 計畫網址：https://www.optml-group.com/posts/deepzero_iclr24

1. 背景

• 零階（Zeroth-Order, ZO）優化已成為解決機器學習（Machine Learning）問題的熱門技術，特別是在一階（First-Order, FO）資訊難以或無法獲得的情況下：

• 物理和化學等學科：機器學習模型可能與複雜的模擬器或實驗相互作用，其中底層系統是不可求導的。

黑盒學習場景：當深度學習（Deep Learning）模型與第三方API 整合時，例如針對黑盒子深度學習模型的對抗性攻擊和防禦，以及語言模型服務的黑盒提示學習。

硬體限制

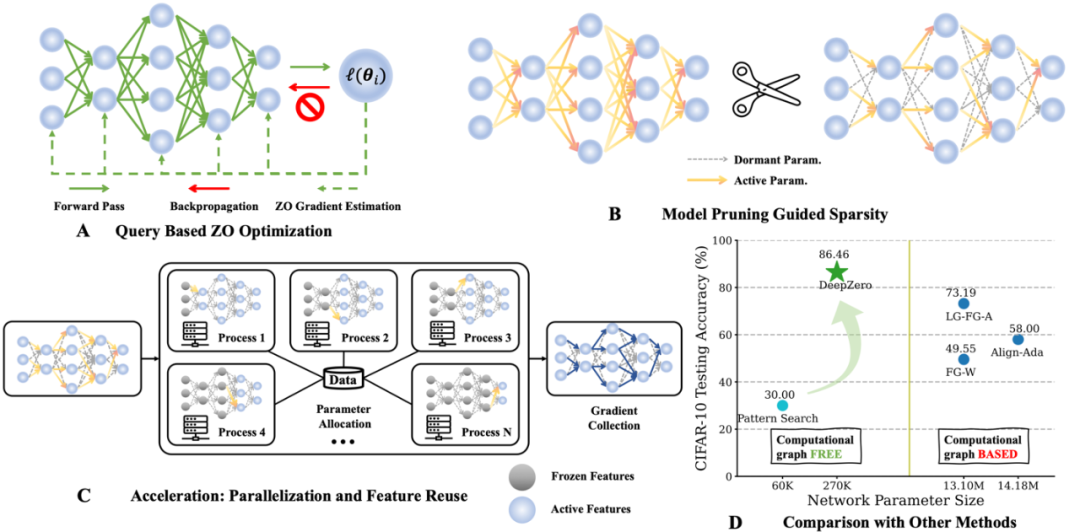
：用於計算一階梯度的原理性反向傳播（backpropagation）機制在硬體系統上實現深度學習模型時可能不受支持。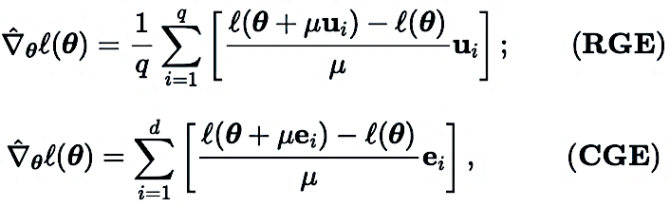

然而，目前零階最佳化的可擴展性仍然是一個未解決的問題：其使用主要限於相對較小規模的機器學習問題，如樣本級的對抗性攻擊生成。隨著問題維度的增加，傳統零階方法的準確性和效率會下降。這是因為基於零階有限差分的梯度估計是一階梯度的有偏估算，且在高維度空間中偏差更加明顯。這些挑戰激發了本文討論的核心問題：

如何擴展零階最佳化使其可以訓練深度學習模型？

2. 零階梯度估算：RGE 還是 CGE？

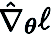
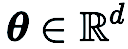
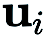
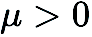零階最佳化器僅透過提交輸入和接收對應的函數值與目標函數進行互動。主要有兩種梯度估算方法：座標梯度估算（Coordinate Gradient Estimation, CGE）和隨機梯度估算（Random Gradient Estimation, RGE），如下所示：

#############其中###表示對最佳化變數###（例如，神經網路的模型參數）的一階梯度的估算。 ######在（RGE）中，###表示隨機擾動向量，例如，從標準高斯分佈中抽取；###是擾動大小（又稱平滑參數）；q 是用於獲得有限差分的隨機方向數。 ###

In (CGE), 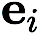represents the standard basis vector, 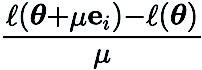provides the finite difference estimate of the partial derivative of 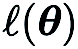at the corresponding coordinates.

Compared with CGE, RGE has the flexibility to reduce the number of function evaluations. Despite its high query efficiency, it is still uncertain whether RGE can provide satisfactory accuracy when training deep models from scratch. To this end, we conducted an investigation in which we trained small convolutional neural networks (CNN) of different sizes on CIFAR-10 using RGE and CGE. As shown in the figure below, CGE can achieve test accuracy comparable to first-order optimization training, and is significantly better than RGE. It is also more time efficient than RGE.

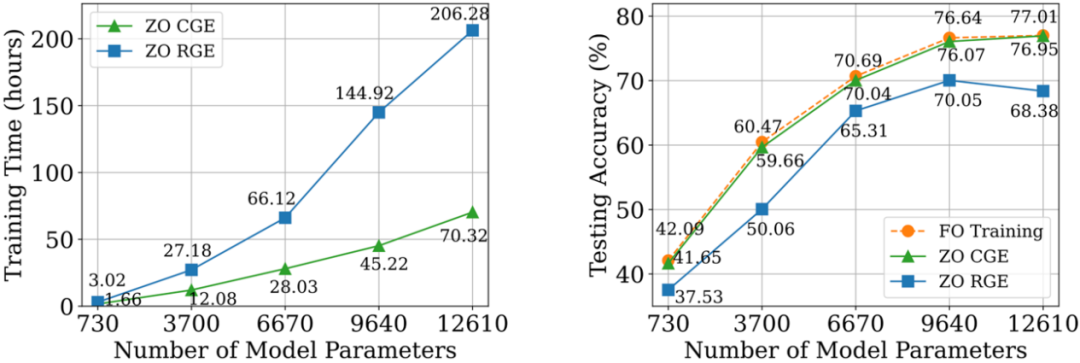
Based on the advantages of CGE over RGE in terms of accuracy and computational efficiency, We choose CGE as the preferred zero-order gradient estimator. However, the query complexity of CGE remains a bottleneck as it scales with model size.

3. Zero-order deep learning framework: DeepZero

As far as we know, previous work has not shown that ZO optimization is not effective when training deep neural networks (DNN). Can significantly reduce performance effectiveness. To overcome this obstacle, we developed DeepZero, a principled zero-order optimization deep learning framework that can extend zero-order optimization to neural network training from scratch.

a) Zero-Order Model Pruning (ZO-GraSP): A randomly initialized dense neural network often contains a high-quality sparse sub-network. However, most effective pruning methods include model training as an intermediate step. Therefore, they are not suitable for finding sparsity via zero-order optimization. To address the above challenges, we are inspired by a training-free pruning method called initialization pruning. Among such methods, Gradient Signal Preserving (GraSP) was chosen, which is a method to identify the sparsity prior of neural networks by randomly initializing the gradient flow of the network.

b) Sparse Gradient: To retain the accuracy benefits of training dense models, in CGE we incorporate gradient sparsity instead of weight sparsity. This ensures that we train a dense model in weight space rather than a sparse model. Specifically, we use ZO-GraSP to determine layer-wise pruning ratios (LPRs) that can capture the compressibility of DNNs, and then zero-order optimization can train densely by continuously iteratively updating some model parameter weights. Model where the sparse gradient ratio is determined by LPRs.

c)

Feature reuse: Since CGE perturbs each parameter element-wise, it can reuse the features immediately before the perturbation layer and perform the remaining forward propagation operations instead of starting from the input layer. Empirically, CGE with feature reuse can achieve more than 2x reduction in training time.

d)

Front-pass parallelization: CGE supports parallelization of model training. This decoupling property makes it possible to scale forward propagation across distributed machines, significantly increasing zero-order training speed.

4. Experimental analysis

a) Image classification

On the CIFAR-10 data set, we train DeepZero ResNet-20 is compared with two variants trained by first-order optimization:

(1) Dense ResNet-20 trained by first-order optimization

(2) Dense ResNet-20 trained by first-order optimization Optimized training of the sparse ResNet-20

obtained through FO-GraSP is shown in the figure below. Although in the 80% to 99% sparse interval, compared with (1), the model trained using DeepZero is still accurate degree gap. This highlights the challenges of ZO optimization for deep model training, where high sparsity implementations are desired. It is worth noting that DeepZero outperforms (2) in the 90% to 99% sparsity interval,

demonstrating the superiority of gradient sparsity over weight sparsity in DeepZero.

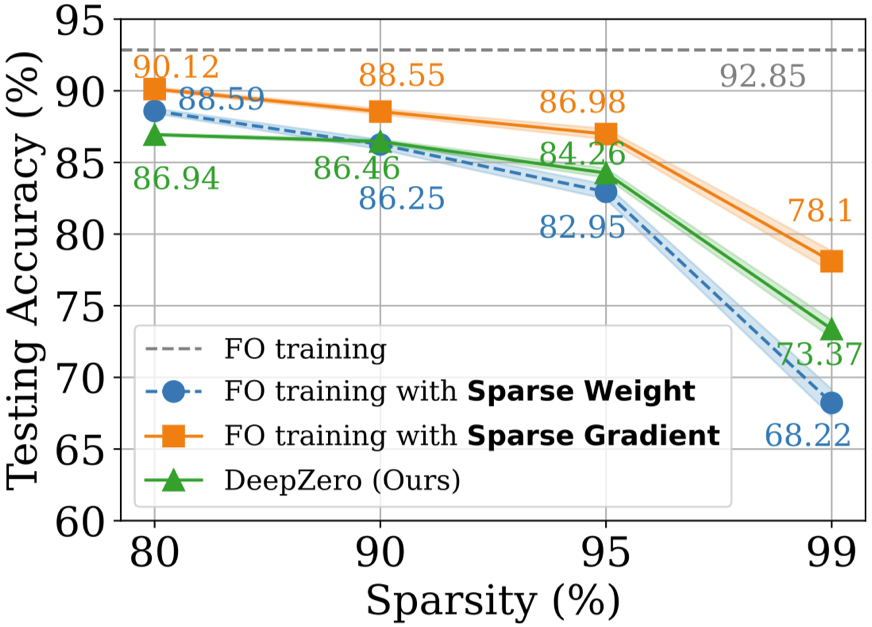
b) Black box defense

The black-box defense problem occurs when the owner of a model is unwilling to share model details with the defender. This poses a challenge to existing robustness enhancement algorithms that directly enhance white-box models using first-order optimization training. To overcome this challenge, ZO-AE-DS is proposed, which introduces an AutoEncoder (AE) between the white-box denoising smoothing (DS) defense operation and the black-box image classifier to solve ZO Dimensional challenges of training. ZO-AE-DS has the disadvantage of being difficult to scale to high-resolution datasets (e.g., ImageNet) because using AE compromises the fidelity of images input to a black-box image classifier and results in poorer defense performance. In contrast, DeepZero can directly learn defensive operations integrated with a black-box classifier, without the need for an autoencoder. As shown in the table below, DeepZero consistently outperforms ZO-AE-DS across all input perturbation radii in terms of Certified Accuracy (CA).

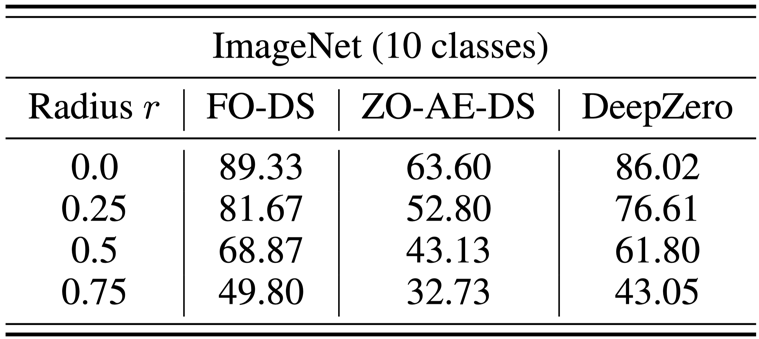
#c) Deep learning coupled with simulation

Numerical methods are indispensable in providing simulations of physical information, but they themselves There are challenges: discretization inevitably produces numerical errors. The feasibility of correcting neural networks through cyclic interactive training with an iterative Partial Differential Equation (PDE) solver is called Solver-in-the-Loop (SOL). While existing work focuses on using or developing differentiable simulators for model training, we extend SOL by leveraging DeepZero to enable use with non-differentiable or black-box simulators. The following table compares the test error correction performance of ZO-SOL (implemented by DeepZero) with three different differentiable methods:

(1) SRC (low-fidelity simulation without error correction);

(2) NON (non-interactive training, performed outside the simulation loop using pre-generated low- and high-fidelity simulation data);

(3) FO-SOL (given differentiable simulations time, used for the first-order training of SOL).

The error for each test simulation is calculated as the mean absolute error (MAE) of the corrected simulation compared to the high-fidelity simulation. Results show that ZO-SOL implemented via DeepZero still outperforms SRC and NON and closes the performance gap with FO-SOL even with only query-based simulator access. The performance of ZO-SOL compared to NON highlights the promise of ZO-SOL when there is black-box simulator integration.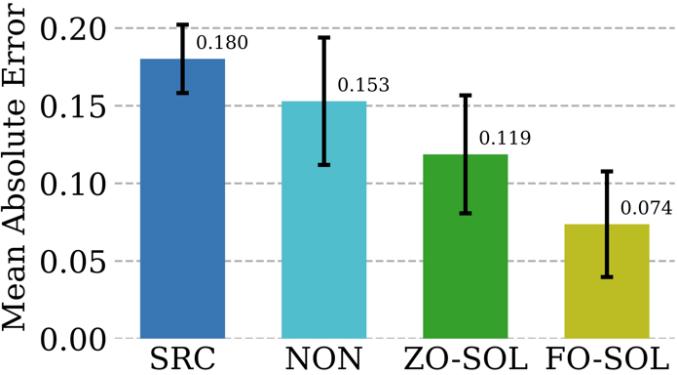

5. Summary and Discussion

This paper introduces a zero-order optimization deep learning framework (DeepZero) for deep network training ). Specifically, DeepZero integrates coordinate gradient estimation, gradient sparsity brought by zero-order model pruning, feature reuse, and front-pass parallelization into a unified training process. Leveraging these innovations, DeepZero has demonstrated efficiency and effectiveness in tasks including image classification and a variety of practical black-box deep learning scenarios. Additionally, the applicability of DeepZero to other areas is explored, such as applications involving non-differentiable physical entities, and training on devices where computational graphs and computations of backpropagation are not supported.

Introduction to the author

Zhang Yimeng, a PhD student in computer science at the OPTML Laboratory of Michigan State University, her research interests include Generative AI, Multi-Modality, Computer Vision, Safe AI, Efficient AI.

以上是ICLR 2024 | 首個零階優化深度學習框架，MSU聯合LLNL提出DeepZero的詳細內容。更多資訊請關注PHP中文網其他相關文章！