
求導鍊式法則是機器學習中的重要數學工具之一。它被廣泛用於線性迴歸、邏輯迴歸、神經網路等演算法。這個法則是微積分中鍊式法則的應用,幫助我們計算函數對某個變數的導數。
複合函數f(x)由多個簡單函數組成,每個簡單函數都對x有導數。根據鍊式法則,f(x)對x的導數可以透過簡單函數的導數相乘再相加得到。
形式化的表示為:如果y=f(u)且u=g(x),那麼y對x的導數dy/dx=f'(u)*g '(x)。
這個公式表明,透過了解簡單函數對x的導數和它們的組合方式,我們可以計算複合函數對x的導數。
求導鍊式法則在最佳化演算法中扮演關鍵角色,特別是在梯度下降等最佳化演算法中。它被用於更新模型參數以最小化損失函數。鍊式法則的核心思想是,如果一個函數是由多個簡單函數組合而成,那麼這個函數對某個變數的導數可以透過每個簡單函數對變數的導數乘積來得到。在機器學習中,這項法則被廣泛應用於計算損失函數對模型參數的梯度。這種方法的有效性使得我們能夠透過反向傳播演算法有效地訓練深度神經網路。
在機器學習中,我們經常需要對參數進行最佳化,這涉及到求解損失函數對參數的導數。而損失函數通常是由多個簡單函數組合而成的複合函數,因此我們需要使用鍊式法則來計算損失函數對參數的導數。
假設我們有一個簡單的線性迴歸模型,模型的輸出y是輸入x的線性組合,也就是y=Wx b,其中W和b是模型的參數。如果我們有一個損失函數L(y,t),其中t是真實標籤,我們可以透過鍊式法則計算損失函數對模型參數的梯度:
dL/dW= dL/dy*dy/dW
dL/db=dL/dy*dy/db
其中,dL/dy是損失函數輸出的導數,dy/dW和dy/db是模型的輸出對參數的導數。透過這個公式,我們可以計算出損失函數對模型參數的梯度,進而使用梯度下降等優化演算法更新模型的參數以最小化損失函數。
在更複雜的模型中,如神經網絡,鍊式法則同樣被廣泛應用。神經網路通常由多個非線性層和線性層組成,每個層都有自己的參數。為了優化模型的參數以最小化損失函數,我們需要使用鍊式法則計算損失函數對每個參數的梯度。
總之,求導鍊式法則是機器學習中非常重要的數學工具之一,它可以幫助我們計算複合函數對某個變數的導數,進而用於最佳化模型的參數以最小化損失函數。
以上是機器學習中的鍊式求導法則的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 7強大的AI提示每個項目經理現在需要掌握May 08, 2025 am 11:39 AM
7強大的AI提示每個項目經理現在需要掌握May 08, 2025 am 11:39 AM聊天機器人像Chatgpt這樣的聊天機器人舉例說明了生成的AI,為項目經理提供了功能強大的工具來簡化工作流程並確保項目按計劃和預算範圍內保持。 但是,在製作正確的提示時有效使用鉸鏈。 精確,細節
 通過AI本身的有益協助,定義難以捉摸的AGI的含義不明的含義May 08, 2025 am 11:37 AM
通過AI本身的有益協助,定義難以捉摸的AGI的含義不明的含義May 08, 2025 am 11:37 AM定義人工智能(AGI)的挑戰是重大的。 AGI進步的主張通常缺乏明確的基準,其定義是針對預定的研究方向而定制的。本文探討了一種新穎的定義方法
 IBM認為2025展示watsonx.data在生成AI中的作用May 08, 2025 am 11:32 AM
IBM認為2025展示watsonx.data在生成AI中的作用May 08, 2025 am 11:32 AMIBM WATSONX.DATA:簡化企業AI數據堆棧 IBM將WATSONX.DATA定位為企業的關鍵平台,旨在加速精確而可擴展的生成AI解決方案。 這是通過簡化投訴來實現的
 人形機器人機器的崛起即將到來。May 08, 2025 am 11:29 AM
人形機器人機器的崛起即將到來。May 08, 2025 am 11:29 AM在AI和材料科學領域的突破所推動的機器人技術的快速進步已準備好迎來人類機器人的新時代。 多年來,工業自動化一直是主要重點,但是機器人的功能迅速exp
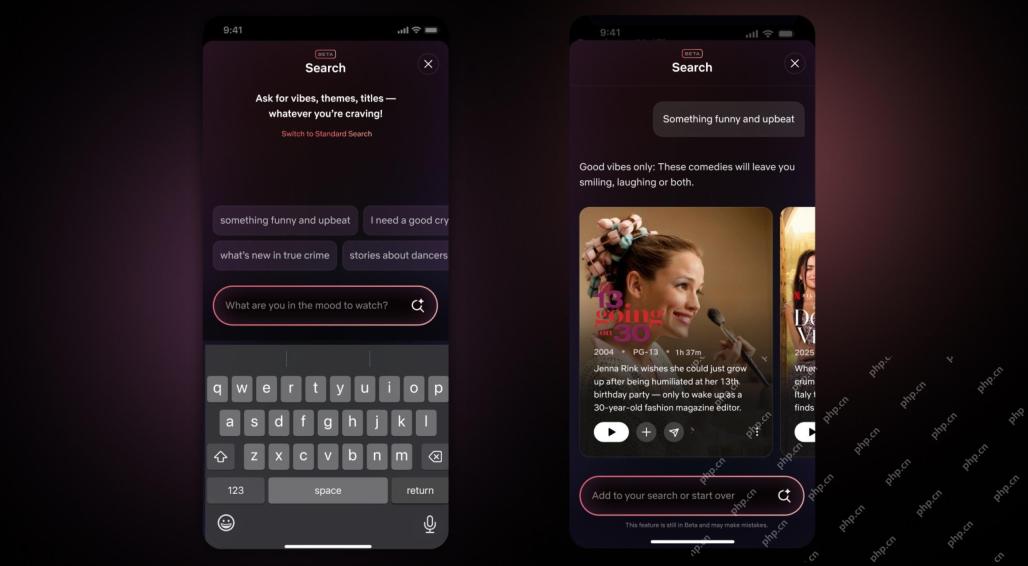 Netflix重新修改界面 - 首次亮相AI搜索工具和類似Tiktok的設計May 08, 2025 am 11:25 AM
Netflix重新修改界面 - 首次亮相AI搜索工具和類似Tiktok的設計May 08, 2025 am 11:25 AMNetflix 界面十年來最大更新:更智能、更個性化,擁抱多元內容 Netflix 週三宣布對其用戶界面進行十年來最大規模的改版,不僅外觀煥然一新,還增加了更多關於每個節目的信息,並引入了更智能的 AI 搜索工具,能夠理解模糊的概念(例如“氛圍”),以及更靈活的結構,以便更好地展示公司在新興的視頻遊戲、直播活動、體育賽事和其他新型內容方面的興趣。 為了緊跟潮流,新的移動端豎屏視頻組件將使粉絲更容易滾動瀏覽預告片和片段,觀看完整節目或與他人分享內容。這讓人聯想起無限滾動且非常成功的短視頻網站 Ti
 在AGI之前很久:三個AI里程碑會挑戰您May 08, 2025 am 11:24 AM
在AGI之前很久:三個AI里程碑會挑戰您May 08, 2025 am 11:24 AM人工智能通用智能(AGI)的討論日益增多,促使許多人思考當人工智能超越人類智能時會發生什麼。這個時刻是近在咫尺還是遙遙無期,取決於你問誰,但我認為這並非我們應該關注的最重要的里程碑。哪些更早的人工智能里程碑會影響到每個人?哪些里程碑已經實現?以下是我認為已經發生的三件事。 人工智能超越人類弱點 在2022年的電影《社交困境》中,人文科技中心(Center for Humane Technology)的崔斯坦·哈里斯指出,人工智能已經超越了人類的弱點。這是什麼意思?這意味著人工智能已經能夠運用人類
 Venkat Achanta在Transunion的平台轉型和AI野心May 08, 2025 am 11:23 AM
Venkat Achanta在Transunion的平台轉型和AI野心May 08, 2025 am 11:23 AMTransunion的首席技術官Ranganath Achanta在2021年末加入公司後加入公司以來,率先進行了重大的技術轉變。
 當對AI的信任躍升時,生產力會隨之而來May 08, 2025 am 11:11 AM
當對AI的信任躍升時,生產力會隨之而來May 08, 2025 am 11:11 AM建立信任至關重要,對於成功採用業務的AI是至關重要的。 考慮到業務流程中的人類因素,這尤其如此。 像其他任何人一樣,員工對AI及其實施引起了人們的關注。 德勤研究人員是SC


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

SublimeText3 Linux新版
SublimeText3 Linux最新版

WebStorm Mac版
好用的JavaScript開發工具

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境

MantisBT
Mantis是一個易於部署的基於Web的缺陷追蹤工具,用於幫助產品缺陷追蹤。它需要PHP、MySQL和一個Web伺服器。請查看我們的演示和託管服務。

SublimeText3漢化版
中文版,非常好用





