
基於物理資訊的神經網路(PINN)是一種結合實體模型和神經網路的方法。透過將物理方法融入神經網路中,PINN可以學習非線性系統的動力學行為。相較於傳統的基於實體模型的方法,PINN具有更高的靈活性和可擴展性。它可以自適應地學習複雜的非線性動力學系統,並同時滿足物理規範的要求。本文將介紹PINN的基本原理,並提供一些實際應用範例。
PINN的基礎是將物理方法融入神經網絡,以學習系統的動力學行為。具體來說,我們可以將物理方法表示為以下形式:
F(u(x),\frac{\partial u}{\partial x},x,t) =0
我們的目標是透過學習系統狀態變化u(x)的時間演化以及系統週邊的邊界條件,來實現對系統行為的理解。為了達到這個目標,我們可以利用神經網路模擬狀態變化u(x)的發展,並使用自動微分技術計算狀態變化的梯度。同時,我們也可以使用物理方法來約束神經網路與狀態變化之間的關係。這樣,我們就能夠更好地理解系統的狀態演化和預測未來的變化。
具體而言,我們可以使用如下的損失函數來訓練PINN:
L_{pinn}=L_{資料} L_{物理}
其中L_{data}是資料遺失,用來模擬已經知道的狀態變化值。通常,我們可以使用均方誤差來確定義L_{data}:
L_{data}=\frac{1}{N}\sum_{i=1}^{ N}(u_i-u_{data,i})^2
其中$N$是資料集中的樣本數,u_i是神經網路預測的狀態變化值,u_{data ,i}是資料集中對應的真實狀態變化值。
L_{physics}是物理約束損失,使用於保證神經網路和狀態變化滿足物理方法。通常,我們可以使用殘差數來確定義L_{物理}:
L_{物理}=\frac{1}{N}\sum_{i=1}^{ N}(F(u_i,\frac{\partial u_i}{\partial x},x_i,t_i))^2
其中F是物理方法,\frac{\partial u_i}{\partial x}是神經網路預測的狀態變化量的坡度,x_i和t_i是類似本i的空間和時間座標。
透過最小化L_{pinn},我們可以同時模擬資料和滿足物理方法,從而學習系統的動力學行為。
現在我們來看一些現實的PINN的示範。其中一個典型的例子是學習Navier-Stokes方法的動力學行為。 Navier-Stokes方法描述了流體的運動行為,它可以寫成如下的形式:
#\rho(\frac{\partial u}{\partial t} u\cdot\nabla u)=-\nabla p \mu\nabla^2u f
其中\rho是流體的密度,u是流體的速度,p是流體的壓力,\mu是流體的密度,f是外部力。我們的目標是學習流體的速度和壓力的時間演化,以及在流體邊界上的邊界條件。
為了實現這個目標,我們可以將Navier-Stokes方法填入神經網路中,以方便學習速度和壓力的時間演化。具體而言,我們可以使用以下的損失敗數來訓練PINN:
L_{pinn}=L_{資料} L_{物理}
##其中L_{data}和L_{physics}的定義與前文相同。我們可以使用流體力學模型產生一組包含速度和壓力的狀態變數數據,然後使用PINN來模擬狀態變化並滿足Navier-Stokes方法。這樣,我們就可以以學習流動體的動力學行為,包括濕流、渦旋和邊界層等現象,而無需先確定正義複雜的物理模型或手動推導解析。
另一個例子是學習非線性波運動方法的運動學行為。非線性波運動方法描述了波運動在介紹中的傳播行為,它可以寫成如下的形式:
#\frac{\partial^2u}{\partial t^2} -c^2\nabla^2u f(u)=0
其中u是波速的幅度,c是波速,f(u)是非線性質的項目。我們的目標是學習波動態的時間演化和在介紹邊界上的邊界條件。
為了實現這個目標,我們可以將非線性波過程納入神經網路中,以方便學習波運動的時代演化。具體而言,我們可以使用如下的損毀數來訓練PINN:
L_{pinn}=L_{資料} L_{物理}
其中L_{data}和L_{physics}的定義與前文相同。我們可以使用數值方法產生一組包含波幅和台階的狀態變化數據,然後用PINN來模擬狀態變化量和滿足非線性波動方法。這樣,我們就可以學習波動在介質中的時間演化,包括波包的形狀變化、折射和反射等現象,而無需先定義複雜的物理模型或手動推導解析。
#######總之,基於物理資訊的神經網路是一種結合物理模型和神經網路的方法,它可以適應地球學習複雜的非線動力學系統,同時保持對物理規律的嚴格滿足。 PINN已被廣泛應用於流體力學、聲學、結構力學等領域,並取得了一些顯著的結果。未來,隨著神經網路和自動化微分技術的不發展,PINN將有希望成為更大更強更通用的工具,用於解決各種非線性動力學問題。
以上是物理資訊驅動的神經網路介紹的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM
解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM二元神经网络(BinaryNeuralNetworks,BNN)是一种神经网络,其神经元仅具有两个状态,即0或1。相对于传统的浮点数神经网络,BNN具有许多优点。首先,BNN可以利用二进制算术和逻辑运算,加快训练和推理速度。其次,BNN减少了内存和计算资源的需求,因为二进制数相对于浮点数来说需要更少的位数来表示。此外,BNN还具有提高模型的安全性和隐私性的潜力。由于BNN的权重和激活值仅为0或1,其模型参数更难以被攻击者分析和逆向工程。因此,BNN在一些对数据隐私和模型安全性有较高要求的应用中具
 探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM
探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM在时间序列数据中,观察之间存在依赖关系,因此它们不是相互独立的。然而,传统的神经网络将每个观察看作是独立的,这限制了模型对时间序列数据的建模能力。为了解决这个问题,循环神经网络(RNN)被引入,它引入了记忆的概念,通过在网络中建立数据点之间的依赖关系来捕捉时间序列数据的动态特性。通过循环连接,RNN可以将之前的信息传递到当前观察中,从而更好地预测未来的值。这使得RNN成为处理时间序列数据任务的强大工具。但是RNN是如何实现这种记忆的呢?RNN通过神经网络中的反馈回路实现记忆,这是RNN与传统神经
 计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PM
计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PMFLOPS是计算机性能评估的标准之一,用来衡量每秒的浮点运算次数。在神经网络中,FLOPS常用于评估模型的计算复杂度和计算资源的利用率。它是一个重要的指标,用来衡量计算机的计算能力和效率。神经网络是一种复杂的模型,由多层神经元组成,用于进行数据分类、回归和聚类等任务。训练和推断神经网络需要进行大量的矩阵乘法、卷积等计算操作,因此计算复杂度非常高。FLOPS(FloatingPointOperationsperSecond)可以用来衡量神经网络的计算复杂度,从而评估模型的计算资源使用效率。FLOP
 模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM
模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM模糊神经网络是一种将模糊逻辑和神经网络结合的混合模型,用于解决传统神经网络难以处理的模糊或不确定性问题。它的设计受到人类认知中模糊性和不确定性的启发,因此被广泛应用于控制系统、模式识别、数据挖掘等领域。模糊神经网络的基本架构由模糊子系统和神经子系统组成。模糊子系统利用模糊逻辑对输入数据进行处理,将其转化为模糊集合,以表达输入数据的模糊性和不确定性。神经子系统则利用神经网络对模糊集合进行处理,用于分类、回归或聚类等任务。模糊子系统和神经子系统之间的相互作用使得模糊神经网络具备更强大的处理能力,能够
 改进的RMSprop算法Jan 22, 2024 pm 05:18 PM
改进的RMSprop算法Jan 22, 2024 pm 05:18 PMRMSprop是一种广泛使用的优化器,用于更新神经网络的权重。它是由GeoffreyHinton等人在2012年提出的,并且是Adam优化器的前身。RMSprop优化器的出现主要是为了解决SGD梯度下降算法中遇到的一些问题,例如梯度消失和梯度爆炸。通过使用RMSprop优化器,可以有效地调整学习速率,并且自适应地更新权重,从而提高深度学习模型的训练效果。RMSprop优化器的核心思想是对梯度进行加权平均,以使不同时间步的梯度对权重的更新产生不同的影响。具体而言,RMSprop会计算每个参数的平方
 浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM
浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM深度学习在计算机视觉领域取得了巨大成功,其中一项重要进展是使用深度卷积神经网络(CNN)进行图像分类。然而,深度CNN通常需要大量标记数据和计算资源。为了减少计算资源和标记数据的需求,研究人员开始研究如何融合浅层特征和深层特征以提高图像分类性能。这种融合方法可以利用浅层特征的高计算效率和深层特征的强表示能力。通过将两者结合,可以在保持较高分类准确性的同时降低计算成本和数据标记的要求。这种方法对于那些数据量较小或计算资源有限的应用场景尤为重要。通过深入研究浅层特征和深层特征的融合方法,我们可以进一
 蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM
蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM模型蒸馏是一种将大型复杂的神经网络模型(教师模型)的知识转移到小型简单的神经网络模型(学生模型)中的方法。通过这种方式,学生模型能够从教师模型中获得知识,并且在表现和泛化性能方面得到提升。通常情况下,大型神经网络模型(教师模型)在训练时需要消耗大量计算资源和时间。相比之下,小型神经网络模型(学生模型)具备更高的运行速度和更低的计算成本。为了提高学生模型的性能,同时保持较小的模型大小和计算成本,可以使用模型蒸馏技术将教师模型的知识转移给学生模型。这种转移过程可以通过将教师模型的输出概率分布作为学生
 SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PM
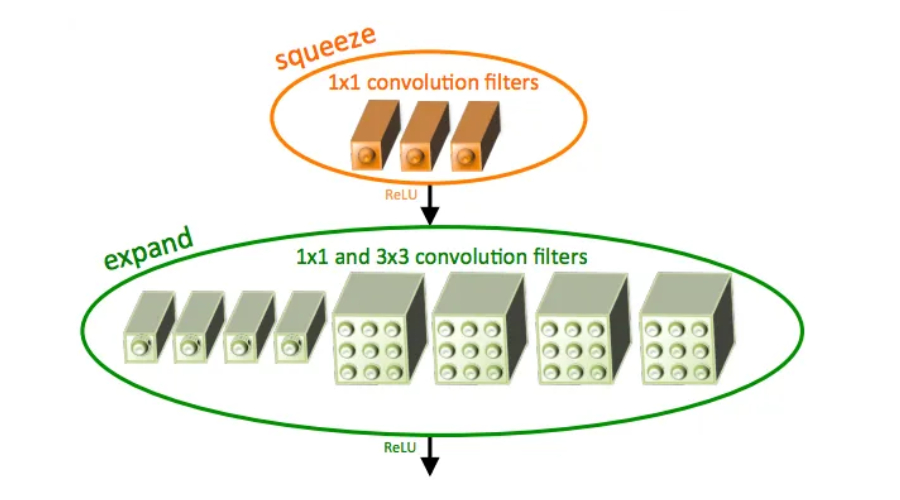
SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PMSqueezeNet是一种小巧而精确的算法,它在高精度和低复杂度之间达到了很好的平衡,因此非常适合资源有限的移动和嵌入式系统。2016年,DeepScale、加州大学伯克利分校和斯坦福大学的研究人员提出了一种紧凑高效的卷积神经网络(CNN)——SqueezeNet。近年来,研究人员对SqueezeNet进行了多次改进,其中包括SqueezeNetv1.1和SqueezeNetv2.0。这两个版本的改进不仅提高了准确性,还降低了计算成本。SqueezeNetv1.1在ImageNet数据集上的精度


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

MinGW - Minimalist GNU for Windows
這個專案正在遷移到osdn.net/projects/mingw的過程中,你可以繼續在那裡關注我們。 MinGW:GNU編譯器集合(GCC)的本機Windows移植版本,可自由分發的導入函式庫和用於建置本機Windows應用程式的頭檔;包括對MSVC執行時間的擴展,以支援C99功能。 MinGW的所有軟體都可以在64位元Windows平台上運作。

SublimeText3 英文版
推薦:為Win版本,支援程式碼提示!

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境





