
在機器學習任務中,損失函數是評估模型表現的重要指標,用於衡量模型預測結果與真實結果之間的差異。交叉熵是一種常見的損失函數,廣泛應用於分類問題。它透過計算模型預測結果與真實結果之間的差異來衡量模型的準確性。稀疏交叉熵是交叉熵的擴展形式,主要用於解決分類問題中的類別不平衡情況。在選擇損失函數時,需要考慮資料集的特徵和模型的目標。交叉熵適用於一般的分類問題,而稀疏交叉熵較適用於處理類別不平衡的情況。選擇合適的損失函數可以提高模型的效能和泛化能力,進而提高機器學習任務的效果。
一、交叉熵
交叉熵是分類問題中常用的損失函數,用來測量模型預測與真實結果之間的差距。它是一種衡量預測結果與真實結果差異的有效指標。
H(p,q)=-\sum_{i=1}^{n}p_i\log(q_i)
其中,p代表真實結果的機率分佈,q代表模型預測結果的機率分佈,n代表類別數。較小的交叉熵值表示模型預測與真實結果之間的差距較小。
交叉熵的優點是可以直接最佳化模型的預測機率分佈,因此可以得到更精確的分類結果。此外,交叉熵有一個很好的性質,就是當模型的預測結果與真實結果完全一致時,交叉熵的值為0。因此,交叉熵可以作為模型訓練過程中的評估指標,用來監控模型的表現。
二、稀疏交叉熵
稀疏交叉熵是交叉熵的擴展形式,用於解決分類問題中的類別不平衡問題。在分類問題中,有些類別可能會比其他類別更常見,這會導致模型更容易預測常見類別,而對於不常見的類別則預測不準確。為了解決這個問題,可以使用稀疏交叉熵作為損失函數,它會對不同類別的預測結果進行加權,使得模型更關注不常見的類別。
稀疏交叉熵的定義如下:
#H(p,q)=-\sum_{i=1}^{n} \alpha_ip_i\log(q_i)
其中,p表示真實結果的機率分佈,q表示模型預測結果的機率分佈,n表示類別的數量,\alpha是權重向量,用於調整不同類別的權重。如果某個類別很常見,那麼它的權重就會比較小,模型就會更關注不常見的類別。
稀疏交叉熵的優點是可以解決分類問題中的類別不平衡問題,使得模型更關注不常見的類別。此外,稀疏交叉熵也可以作為模型訓練過程中的評估指標,用來監控模型的表現。
三、如何選擇交叉熵和稀疏交叉熵
在選擇交叉熵和稀疏交叉熵時,需要考慮資料集的特點以及模型的目標。
如果資料集中的類別相對平衡,那麼可以使用交叉熵作為損失函數。交叉熵可以直接優化模型的預測機率分佈,因此可以得到更精確的分類結果。此外,交叉熵也可以作為模型訓練過程中的評估指標,用來監控模型的表現。
如果資料集中的類別不平衡,那麼可以考慮使用稀疏交叉熵作為損失函數。稀疏交叉熵可以解決分類問題中的類別不平衡問題,使得模型更關注不常見的類別。此外,稀疏交叉熵也可以作為模型訓練過程中的評估指標,用來監控模型的表現。
在選擇稀疏交叉熵時,需要根據資料集中不同類別的權重來設定權重向量\alpha。一般來說,可以根據不同類別的樣本數量來設定權重,使得樣本數量較少的類別的權重較大,樣本數量較多的類別的權重較小。在實踐中,可以透過交叉驗證等方法來確定權重向量的值。
要注意的是,在選擇損失函數時,還需要考慮模型的目標。例如,在一些模型中,需要最佳化的是分類準確率而不是交叉熵或稀疏交叉熵。因此,在選擇損失函數時,需要綜合考慮資料集的特性和模型的目標,選擇最適合的損失函數來評估模型的效能。
總之,交叉熵和稀疏交叉熵都是常見的損失函數,可以用來分類問題。在選擇損失函數時,需要考慮資料集的特性和模型的目標,選擇最適合的損失函數來評估模型的效能。同時,在實務中,還需要透過交叉驗證等方法來確定損失函數的參數值,以獲得更好的效能。
以上是如何選擇機器學習任務中的交叉熵和稀疏交叉熵?的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM
Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM處理文檔不再只是在您的AI項目中打開文件,而是將混亂變成清晰度。諸如PDF,PowerPoints和Word之類的文檔以各種形狀和大小淹沒了我們的工作流程。檢索結構化
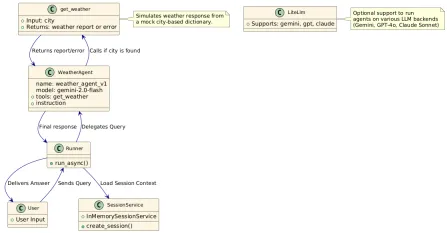 如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM
如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM利用Google的代理開發套件(ADK)的力量創建具有現實世界功能的智能代理!該教程通過使用ADK來構建對話代理,並支持Gemini和GPT等各種語言模型。 w
 在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM
在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM摘要: 小型語言模型 (SLM) 專為效率而設計。在資源匱乏、實時性和隱私敏感的環境中,它們比大型語言模型 (LLM) 更勝一籌。 最適合專注型任務,尤其是在領域特異性、控制性和可解釋性比通用知識或創造力更重要的情況下。 SLM 並非 LLMs 的替代品,但在精度、速度和成本效益至關重要時,它們是理想之選。 技術幫助我們用更少的資源取得更多成就。它一直是推動者,而非驅動者。從蒸汽機時代到互聯網泡沫時期,技術的威力在於它幫助我們解決問題的程度。人工智能 (AI) 以及最近的生成式 AI 也不例
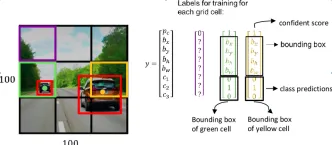 如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM
如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM利用Google雙子座的力量用於計算機視覺:綜合指南 領先的AI聊天機器人Google Gemini擴展了其功能,超越了對話,以涵蓋強大的計算機視覺功能。 本指南詳細說明瞭如何利用
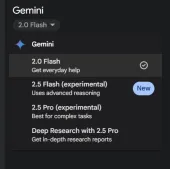 Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM2025年的AI景觀正在充滿活力,而Google的Gemini 2.0 Flash和Openai的O4-Mini的到來。 這些尖端的車型分開了幾週,具有可比的高級功能和令人印象深刻的基準分數。這個深入的比較
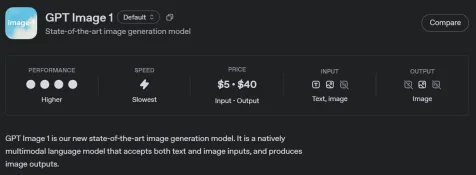 如何使用OpenAI GPT-Image-1 API生成和編輯圖像Apr 27, 2025 am 09:16 AM
如何使用OpenAI GPT-Image-1 API生成和編輯圖像Apr 27, 2025 am 09:16 AMOpenai的最新多模式模型GPT-Image-1徹底改變了Chatgpt和API的形像生成。 本文探討了其功能,用法和應用程序。 目錄 了解gpt-image-1 gpt-image-1的關鍵功能
 如何使用清潔行執行數據預處理? - 分析VidhyaApr 27, 2025 am 09:15 AM
如何使用清潔行執行數據預處理? - 分析VidhyaApr 27, 2025 am 09:15 AM數據預處理對於成功的機器學習至關重要,但是實際數據集通常包含錯誤。清潔行提供了一種有效的解決方案,它使用其Python軟件包來實施自信的學習算法。 它自動檢測和
 AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM
AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM經常使用“ AI-Ready勞動力”一詞,但是在供應鏈行業中確實意味著什麼? 供應鏈管理協會(ASCM)首席執行官安倍·埃什肯納齊(Abe Eshkenazi)表示,它表示能夠評論家的專業人員


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

Atom編輯器mac版下載
最受歡迎的的開源編輯器

SAP NetWeaver Server Adapter for Eclipse
將Eclipse與SAP NetWeaver應用伺服器整合。

Dreamweaver Mac版
視覺化網頁開發工具

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

WebStorm Mac版
好用的JavaScript開發工具





