如何函數中的自變數的取值範圍

如何函數中的自變數的取值範圍

(1)、解析式為整數的，自變數可取任意實數；

解析式中的分式，自變數應取非零實數值。

(3)、對於解析式是二次根式或偶次根式的情況，我們需要將自變數取被開方數不小於0的實數。這樣才能保證解析式有意義且可求解。

(4)、對於函數解析式複雜的複合函數，應全面考慮，確保解析式中的各個元素都有意義。在進行計算之前，我們需要仔細分析每個函數的定義域和值域，以確保整個複合函數的解析式是有意義的。這樣可以避免在計算過程中出現錯誤或無法確定的情況。

在解類似y=1/x √(3x-1)的方程式時，我們需要考慮函數的實際意義，並決定自變數的取值範圍。對於這個方程，它的自變數x的取值範圍應滿足x≥1/3.2，以確保函數在實際意義上有意義。這樣，我們可以更好地解決問題並得到正確的結果。

函數變數與其他變數等整數類似，本身沒有實際意義，只是用來取代目標。函數變數包括自變數和因變數。自變量是在一定取值範圍內（定義域）任意取值的變量，而因變量則是根據函數法則在自變量取值後得到的變量。

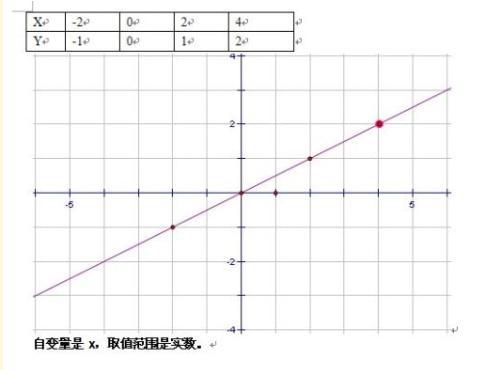
#擴充資料：

自變數的取值範圍指的是函數中使其有意義的自變數取值的全體。在數學中，我們定義了函數的自變數的取值範圍，以確保函數在這個範圍內是有意義的。這個範圍可以是實數集、整數集、有理數集或其他特定的數值範圍，取決於函數的定義和要求。

自變數的取值範圍的決定方法：

首先，我們需要考慮自變數的取值範圍，以確保解析式有意義。如果解析式是整式，那麼自變數可以是任意實數。而如果解析式是分數形式，我們需要確保分母不為零，因此自變數的值範圍就是所有使分母不為零的實數。透過合理選擇自變數的取值範圍，我們能夠確保解析式的有效性。

當解析式中存在平方根時，需要確保被開方數不小於零的實數，這樣才能得到有效的解。而當函數解析式用來表示實際問題時，自變數的取值必須使實際問題有意義，以確保結果的合理性。這樣，我們可以根據這兩個原則來決定自變數的值範圍，從而得到正確的解答。

自變數的取值範圍可以是無限的，有限的，或是單獨一個（或幾個）數。當一個函數解析式中有多個代數式時，函數的自變數的取值範圍應該是各個代數式中自變數取值範圍的公共部分。

函數變數與實際問題：

在解決實際問題的過程中，我們常常會遇到變數和常數的概念。變數和常數往往是相對的，它們的身份可以在不同的研究過程中相互轉換。然而，在處理實際問題時，我們需要注意區分變數和常數的不同。變數是可以改變的，而常數是固定不變的。因此，我們需要根據具體情況來決定何時使用變數和常數，並在解謎過程中靈活運用它們。

接下來，我們可以嘗試尋找變數之間的聯繫，並學習如何使用函數來表示它們。透過這種方式，我們能夠更好地解決謎題，找到通關的方法。

在解決實際問題時，利用函數的圖像是非常關鍵的。我們需要正確理解橫軸和縱軸的意義，了解函數圖象的性質，並且能夠精確地辨識和運用圖象來解決問題。透過這種方法，我們能夠更好地理解函數的特徵和行為，從而更有效地解決各種實際問題。

參考資料：搜狗百科—函數變數

在函數式中怎樣自變數的取值範圍

一、內容綜述：

1.函數的相關概念：

一般情況下，我們在某個變化過程中會牽涉到兩個變數x和y。如果對於x在某個確定範圍內的每個具體值，都有一個唯一對應的y值與之對應，那麼我們稱y是x的函數，而x則稱為自變數。

對於函數的意義，應從以下幾個面向去理解：

我們在研究某個變化過程中，探究兩個變項之間的函數關係。在不同的研究過程中，變數和常數可以互相轉換，即常數和變數是相對於某個過程而言的。這種相互轉換的靈活性使得我們能夠更好地理解和分析變數之間的關係。

(2) 變數x的取值範圍是由允許的每個值組成的。 (3) 變數x和y之間有確定的對應關係，即對於x的每個允許值，都存在唯一的y值與之對應。

怎麼理解相同的函數：

函數的概念可以理解為，當變數x與變數y之間存在著一種特殊的對應關係時（即對應法則），在變數x的取值範圍內，每個x值都對應到唯一的y值，那麼變數y就是變數x的函數。簡言之，函數的概念包含以下兩個要點：

(1)y與x之間的函數關係式；

(2)函數關係式中自變數x的取值範圍。

這就是說，相同的函數必須要以上兩個面向都滿足，即函數關係式相同（或變形後相同），自變數x的取值範圍也相同，否則，就不是相同的函數。而其中函數關係式相同與否比較容易注意到，自變數x的值範圍有時容易忽視，這點請同學注意。

下列函數中，與y=x表示是同一函數關係的是（ ）。

解謎方法：首先，我們需要將四個函數的解析式進行簡化，並與y=x進行比較，看看是否相同。然後，我們需要確定每個函數中自變數x的取值範圍，並將其與y=x的解析式和自變數x的取值範圍進行比較。只有當這兩個條件都滿足時，才是相同的函數。

解：函數y=x，其自變數x的取值範圍為全體實數。

， 其自變數x的取值範圍是x≥0的一切實數。

，其自變數x的取值範圍是x≠0的一切實數。

，其自變數x的取值範圍是一切實數。

，其自變數x的取值範圍是一切實數。

很明顯，只有選項（C）的解析式與y=x的值範圍相同，所以正確答案應該是（C）。

2.函數自變數的取值範圍

函數自變數的取值範圍的原則是：

(1)解析式是整數，自變數可以取一切實數。

解析式是一個分式，因此在決定自變數的取值時，需要避免使分母等於零。這是因為分母為零會導致分式無法計算。要確保解析式的分母不為零，從而得到有效的解答。

對於解析式為無理式的情況，我們需要注意以下兩點： 1. 若是二次根式，被開方式的值應大於或等於零。因此，我們需要找到自變數的取值範圍，使得被開方式大於或等於零。 2. 如果是三次根式，自變數可以取一切實數。這意味著我們可以選擇任何實數作為自變數的取值。 這些注意事項將有助於我們正確解析無理式並確定自變數的取值範圍。

如果解析式是由以上幾種形式綜合而成，那麼自變數的取值範圍就需要同時滿足它們各自的條件。這樣，我們就能更好地解決問題了。

3.函數值

與函數值有關的問題可以轉換為代數式的值。

4.函數的圖象

函數圖象實現了數與形的相互轉換。

以上是如何函數中的自變數的取值範圍的詳細內容。更多資訊請關注PHP中文網其他相關文章！