常用的迴歸演算法及其特點在機器學習中的應用
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB轉載
- 2023-11-29 17:29:26949瀏覽
迴歸是統計學中最有力的工具之一,機器學習監督學習演算法分為分類演算法和迴歸演算法兩種。迴歸演算法用於連續型分佈預測,可以預測連續型資料而不僅僅是離散的類別標籤。
迴歸分析在機器學習領域中廣泛應用,例如預測商品銷售、交通流量、房價以及天氣狀況等
迴歸演算法是一種常用的機器學習演算法,用於建立自變數X和因變數Y之間的關係。從機器學習的角度來看,它用於建立一個演算法模型(函數),以實現屬性X和標籤Y之間的映射關係。在學習過程中,演算法試圖找到最佳的參數關係,以使擬合程度最好
在迴歸演算法中,演算法(函數)的最終結果是一個連續的資料值。輸入值(屬性值)是一個d維度的屬性/數值向量
一些常用的迴歸演算法包括線性迴歸、多項式迴歸、決策樹迴歸、Ridge迴歸、Lasso迴歸、ElasticNet迴歸等等
本文將介紹一些常見的迴歸演算法,以及它們各自的特點
- #線性迴歸
- #多項式迴歸
- 支援向量機迴歸
- 決策樹迴歸
- 隨機森林迴歸
- #LASSO 回歸
- Ridge 回歸
- ElasticNet 回歸
- ##XGBoost 回歸
- 局部加權線性迴歸
線性迴歸通常是人們學習機器學習和資料科學的第一個演算法。線性迴歸是一種線性模型,它假設輸入變數 (X) 和單一輸出變數 (y) 之間存在線性關係。一般來說,有兩種情況:
單變數線性迴歸是一種建模方法,用於分析單一輸入變數(即單一特徵變數)與單一輸出變數之間的關係
多變量線性迴歸(也稱為多元線性迴歸):它對多個輸入變數(多個特徵變數)和單一輸出變數之間的關係進行建模。
關於線性迴歸的幾個關鍵點:
- #快速且易於建模
- 當要建模的關係不是非常複雜且您沒有大量資料時,它特別有用。
- 非常直覺的理解與解釋。
- 它對異常值非常敏感。
當我們想要為非線性可分資料建立模型時,多項式迴歸是最受歡迎的選擇之一。它類似於線性迴歸,但使用變數 X 和 y 之間的關係來找到繪製適合資料點的曲線的最佳方法。
關於多項式迴歸的幾個關鍵點:
- #能夠對非線性可分資料進行建模;線性迴歸不能做到這一點。一般來說,它更加靈活,可以對一些相當複雜的關係進行建模。
- 完全控制特徵變數的建模(要設定的指數)。
- 需要精心設計。需要一些數據知識才能選擇最佳指數。
- 如果指數選擇不當,則容易過度擬合。
支援向量機在分類問題中是眾所周知的。 SVM 在迴歸中的使用稱為支持向量迴歸(SVR)。 Scikit-learn在 SVR()中內建了這種方法。
關於支援向量迴歸的幾個關鍵點:
- #它對異常值具有穩健性,並且在高維空間中有效
- 它具有出色的泛化能力(能夠正確適應新的、以前看不見的數據)
- #如果特徵數遠大於樣本數,則容易過度擬合
決策樹是一種用於分類和迴歸的非參數監督學習方法。目標是創建一個模型,透過學習從資料特徵推斷出的簡單決策規則來預測目標變數的值。一棵樹可以看成是分段常數近似。
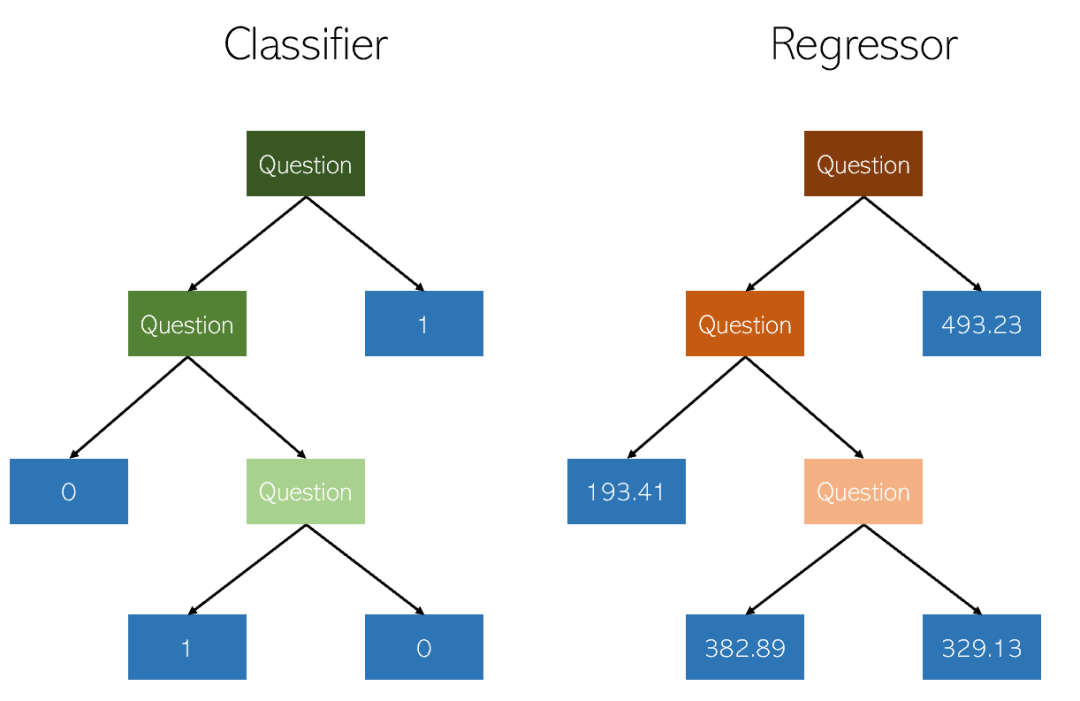
關於決策樹的幾個關鍵點:
- 易於理解和解釋。樹可以可視化。
- 適用於分類值和連續值
- 使用DT(即預測資料)的成本與用於訓練樹的資料點數量成對數
- 決策樹的預測既不平滑也不連續(如上圖所示為分段常數近似)
五、隨機森林迴歸
隨機森林迴歸與決策樹迴歸基本上非常相似。它是一種元估計器,可以在資料集的各個子樣本上擬合多個決策樹,並透過平均來提高預測準確性和控制過擬合
##隨機森林迴歸器在迴歸問題中的表現可能會優於決策樹,也可能不如決策樹(儘管在分類問題中通常更好),這是由於樹構造演算法本身存在微妙的過擬合和欠擬合的權衡
關於隨機森林迴歸的幾點:
- 減少決策樹中的過度擬合並提高準確性。
- 它也適用於分類值和連續值。
- 需要大量運算能力和資源,因為它適合許多決策樹來組合它們的輸出。
LASSO迴歸是一種變體的收縮線性迴歸。收縮是將數據值收縮到中心點作為平均值的過程。這種迴歸類型非常適用於具有嚴重多重共線性(特徵之間高度相關)的模型
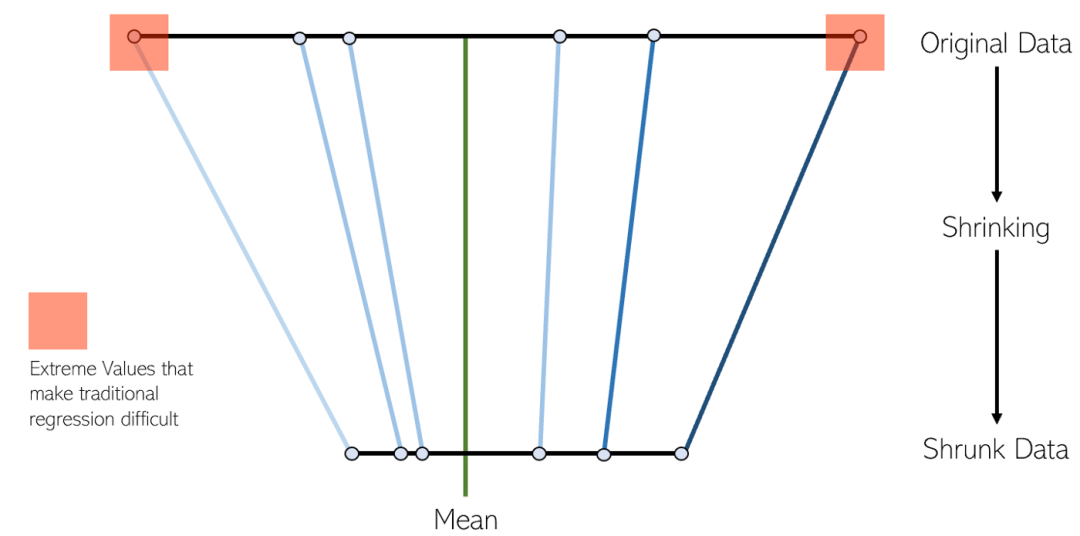
#關於Lasso 迴歸的幾點:
- 它最常用於消除自動變數和選擇特徵。
- 它非常適合顯示重度多重共線性(特徵彼此之間高度相關)的模型。
- LASSO 迴歸利用L1 正規化
- #LASSO 迴歸被認為比Ridge 更好,因為它只選擇了一些特徵並將其他特徵的係數降低到零。
嶺迴歸(Ridge regression)和LASSO迴歸非常相似,因為這兩種技巧都採用了收縮方法。 Ridge和LASSO回歸都非常適合具有嚴重多重共線性問題(即特徵之間高度相關)的模型。它們之間的主要差異在於Ridge使用L2正規化,這意味著沒有一個係數會像LASSO迴歸中那樣變為零(而是接近零)
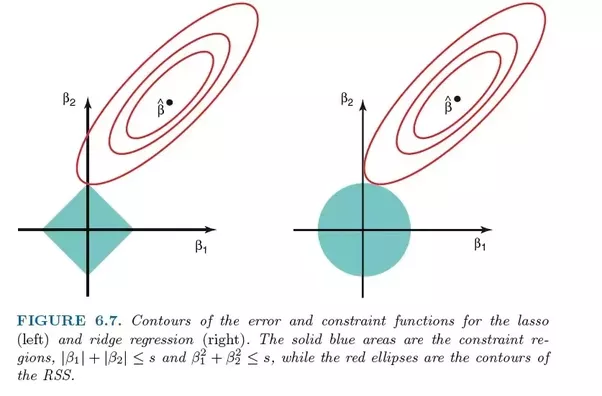
關於嶺迴歸的幾點:
- #它非常適合顯示重度多重共線性(特徵相互之間高度相關)的模型。
- 嶺迴歸使用 L2 正規化。貢獻較小的特徵將具有接近零的係數。
- 由於 L2 正規化的性質,嶺迴歸被認為比 LASSO 更差。
ElasticNet 是另一個使用 L1 和 L2 正規化訓練的線性迴歸模型。它是 Lasso 和 Ridge 回歸技術的混合體,因此它也非常適合顯示重度多重共線性(特徵相互之間高度相關)的模型。
在權衡Lasso和Ridge之間時,一個實際的優勢是Elastic-Net可以在旋轉下繼承Ridge的一些穩定性
九、 XGBoost 迴歸XGBoost 是梯度提升演算法的一種高效且有效的實作。梯度提升是一類可用於分類或迴歸問題的整合機器學習演算法
XGBoost是一個開源函式庫,最初由陳天奇在他於2016年的論文《XGBoost: A Scalable Tree Boosting System》中開發。此演算法的設計旨在具有高效和效率的運算能力
A few points about XGBoost:
- ##XGBoost does not perform well on sparse and unstructured data.
- The algorithm is designed to be computationally efficient and efficient, but the training time is still quite long for large data sets.
- It is sensitive to outliers.
In Local Weights Linear Regression (Local Weights Linear Regression), we are also performing linear regression. However, unlike ordinary linear regression, locally weighted linear regression is a local linear regression method. By introducing weights (kernel functions), when making predictions, only some samples that are close to the test points are used to calculate the regression coefficients. Ordinary linear regression is global linear regression, which uses all samples to calculate the regression coefficient
Advantages, Disadvantages & Applicable Scenarios
##The advantage is to prevent under-fitting through kernel function weighting, but the disadvantage is also obvious that K needs to be debugged. When multiple linear regression is overfitting, you can try Gaussian kernel local weighting to prevent overfitting.11. Bayesian Ridge Regression
The linear regression model solved using the Bayesian inference method is called Bayesian linear regressionBayesian linear regression is a method that treats the parameters of a linear model as random variables and calculates the posterior through the prior. Bayesian linear regression can be solved by numerical methods, and under certain conditions, posterior or related statistics in analytical form can also be obtained
Bayesian linear regression has a Bayesian statistical model The basic properties of it can solve the probability density function of weight coefficients, conduct online learning and model hypothesis testing based on Bayes factor (Bayes factor)
Advantages and Disadvantages&Applicable Scenarios
#The advantage of Bayesian regression is that it has the ability to adapt to data, reuse data and prevent overfitting. In the estimation process, regularization terms can be introduced. For example, by introducing the L2 regularization term in Bayesian linear regression, Bayesian ridge regression can be realized.
The disadvantage is the learning process overhead Too big. When the number of features is less than 10, you can try Bayesian regression.
以上是常用的迴歸演算法及其特點在機器學習中的應用的詳細內容。更多資訊請關注PHP中文網其他相關文章!

