Transformer 已經在自然語言處理、電腦視覺和時間序列預測等領域的各種學習任務中取得成功。雖然取得了成功,但是這些模型仍然面臨嚴重的可擴展性限制。原因是對注意力層的精確計算導致了二次(在序列長度上)的運行時間和記憶體複雜性。這為將Transformer模型擴展到更長的上下文長度帶來了根本性的挑戰
業界已經探索了各種方法來解決二次時間注意力層的問題,其中一個值得注意的方向是近似注意力層中的中間矩陣。實現這一點的方法包括透過稀疏矩陣、低秩矩陣進行近似,或兩者的結合。
然而,這些方法並不能為注意力輸出矩陣的近似提供端對端的保證。這些方法旨在更快地逼近注意力的各個組成部分,但沒有一種方法能提供完整點積注意力的端到端逼近。這些方法還不支援使用因果掩碼,而因果掩碼是現代Transformer架構的重要組成部分。最近的理論邊界表明,在一般情況下,不可能在次二次時間內對注意力矩陣進行分項近似
不過,最近一項名為KDEFormer 的研究表明,在註意力矩陣項有界的假設條件下,它能在次二次時間內提供可證明的近似值。從理論上講,KDEFormer 的運行時大約為 ;它採用核密度估計(kernel density estimation,KDE) 來近似列範數,允許計算對注意力矩陣的列進行採樣的機率。然而,目前的 KDE 演算法缺乏實際效率,即使在理論上,KDEFormer 的運行時與理論上可行的 O (n) 時間演算法之間也有差距。在文中,作者證明了在同樣的有界條目假設下,近線性時間的
;它採用核密度估計(kernel density estimation,KDE) 來近似列範數,允許計算對注意力矩陣的列進行採樣的機率。然而,目前的 KDE 演算法缺乏實際效率,即使在理論上,KDEFormer 的運行時與理論上可行的 O (n) 時間演算法之間也有差距。在文中,作者證明了在同樣的有界條目假設下,近線性時間的 演算法是可能的。不過,他們的演算法還涉及使用多項式方法來逼近 softmax,很可能不切實際。
演算法是可能的。不過,他們的演算法還涉及使用多項式方法來逼近 softmax,很可能不切實際。
而在本文中,來自耶魯大學、Google研究院等機構的研究者提供了一種兩全其美的演算法,既實用高效,又是能實現最佳近線性時間保證。此外,該方法還支援因果掩碼,這在先前的工作中是不可能實現的。

請點擊以下連結查看論文:https://arxiv.org/abs/2310.05869
#本文提出了一種名為「超級注意力(HyperAttention)」的近似注意力機制,旨在應對大型語言模型中使用長上下文所帶來的計算挑戰。最近的研究表明,在最壞的情況下,除非注意力矩陣的條目有界或矩陣的穩定秩較低,否則二次時間是必要的
重寫內容如下:研究者引入了兩個參數來衡量:(1)最大列範數歸一化注意力矩陣,(2)刪除大條目後,非歸一化注意力矩陣中行範數的比例。他們使用這些細粒度參數來反映問題的難易度。只要上述參數很小,即使矩陣具有無界條目或較大的穩定秩,也能夠實現線性時間採樣演算法
超級關注(HyperAttention)具有模組化設計的特點,可以輕鬆整合其他快速底層實現,尤其是FlashAttention。根據經驗,採用LSH演算法來識別大型條目時,超級關注優於現有方法,並且與FlashAttention等最先進解決方案相比,速度有了顯著提高。研究人員在各種不同長度的上下文資料集上驗證了超級關注的效能
例如,HyperAttention 讓ChatGLM2 在32k 上下文長度上的推理時間快了50%,而困惑度從5.6 增加到6.3。在更大的上下文長度(例如 131k)和因果掩碼情況下,HyperAttention 在單一注意力層上速度提升了 5 倍。
方法概覽
點積注意涉及處理三個輸入矩陣: Q (queries) 、K (key)、V (value) ,大小均為nxd,其中n 是輸入序列中的token 數,d 是潛在表徵的維度。這一過程的輸出結果如下:

這裡,矩陣 A := exp (QK^T) 被定義為 QK^T 的元素指數。 D 是一個 n×n 對角矩陣,由 A 各行總和導出, 這裡 。在這種情況下,矩陣 A 被稱為「注意力矩陣」,(D^-1 ) A 被稱為「softmax 矩陣」。值得注意的是,直接計算注意力矩陣 A 需要 Θ(n²d)運算,而儲存它需要消耗 Θ(n²)記憶體。因此,直接計算 Att 需要 Ω(n²d)的運行時和 Ω(n²)的記憶體。
。在這種情況下,矩陣 A 被稱為「注意力矩陣」,(D^-1 ) A 被稱為「softmax 矩陣」。值得注意的是,直接計算注意力矩陣 A 需要 Θ(n²d)運算,而儲存它需要消耗 Θ(n²)記憶體。因此,直接計算 Att 需要 Ω(n²d)的運行時和 Ω(n²)的記憶體。
研究者目標是有效率地近似輸出矩陣 Att,同時保留其頻譜特性。他們的策略包括為對角縮放矩陣 D 設計一個近線性時間的高效估計器。此外,他們透過子取樣快速逼近 softmax 矩陣 D^-1A 的矩陣乘積。更具體地說,他們的目標是找到一個具有有限行數 的取樣矩陣
的取樣矩陣 以及一個對角矩陣
以及一個對角矩陣 # ,從而滿足誤差的算子規範的以下約束:
# ,從而滿足誤差的算子規範的以下約束:

#研究者表明,透過基於V 的行規範定義採樣矩陣S,可以高效解式(1) 中註意力近似問題的矩陣乘法部分。更具挑戰性的問題是:如何獲得對角矩陣 D 的可靠近似值。在最近的成果中,Zandieh 有效地利用了快速 KDE 求解器來獲得 D 的高品質近似值。研究者簡化了 KDEformer 程序,並證明均勻取樣足以實現所需的頻譜保證,而無需基於內核密度的重要性取樣。這項重大簡化使他們開發了一種實用的、可證明的線性時間演算法。
與先前的研究不同,本文方法並不需要有界條目或有界穩定秩。此外,即使注意力矩陣中的條目或穩定秩很大,但為分析時間複雜度而引入的細粒度參數仍可能很小。
因此,HyperAttention 的速度有了顯著提高,在序列長度為 n= 131k 時,前向和後向傳播速度提高了 50 倍以上。在處理因果遮罩時,該方法仍能大幅提高 5 倍的速度。此外,當此方法應用於預先訓練的 LLM (如 chatqlm2-6b-32k )並在長語境基準資料集 LongBench 上進行評估時,即使不需要微調,也能保持與原始模型接近的效能水準。研究者也對特定任務進行了評估,他們發現總結和程式碼完成任務比問題解答任務對近似注意力層的影響更大。
演算法
為了在近似Att 時獲得頻譜保證,本文第一步是對矩陣D 的對角線項進行1 ± ε 近似。隨後,根據 V 的平方行ℓ₂-norms,透過取樣逼近 (D^-1)A 和 V 之間的矩陣乘積。
近似 D 的過程包括兩個步驟。首先,使用植根於 Hamming 排序 LSH 的演算法來識別注意力矩陣中的主要條目,如定義 1 所示。第二步是隨機選擇一小部分 K。本文將證明,在矩陣 A 和 D 的某些溫和假設條件下,這種簡單的方法可以建立估計矩陣的頻譜邊界。研究者的目標是找到一個足夠精確的近似矩陣 D,滿足:

本文的假設是,softmax 矩陣的列範數呈現相對均勻的分佈。更精確地說,研究者假設任意 i ∈ [n] t 存在某個 #,使得
#,使得 。
。
演算法的第一步是使用 Hamming 排序 LSH (sortLSH) 將鍵和查詢雜湊到大小均勻的桶中,從而識別注意力矩陣 A 中的大型條目。演算法 1 詳細介紹了這個過程,圖 1 直觀地說明了這個過程。

演算法 1 的功能是傳回一個稀疏掩碼,用於隔離注意力矩陣的主要條目。在得到該遮罩之後,研究人員可以在演算法 2 中計算矩陣 D 的近似值,該近似值滿足公式 (2) 中的頻譜保證。此演算法的實現方式是將掩碼對應的注意力值與注意力矩陣中隨機選擇的一組列相結合。這篇論文中的演算法可以被廣泛應用,透過使用預先定義的遮罩來指定注意力矩陣中主要條目的位置,可以有效地使用它。此演算法的主要保證在定理1 中給出


#整合近似對角線 與近似
與近似 與值矩陣 V 之間矩陣乘積的子程式。因此,研究者引入了 HyperAttention,這是一種高效能演算法,可以在近似線性時間內近似公式(1)中具有頻譜保證的注意力機制。演算法 3 將定義注意力矩陣中主導條目的位置的遮罩 MH 作為輸入。這個掩碼可以使用 sortLSH 演算法(演算法 1)生成,也可以是一個預先定義的掩碼,類似於 [7] 中的方法。研究者假定大條目遮罩 M^H 在設計上是稀疏的,且其非零條目數是有界的
與值矩陣 V 之間矩陣乘積的子程式。因此,研究者引入了 HyperAttention,這是一種高效能演算法,可以在近似線性時間內近似公式(1)中具有頻譜保證的注意力機制。演算法 3 將定義注意力矩陣中主導條目的位置的遮罩 MH 作為輸入。這個掩碼可以使用 sortLSH 演算法(演算法 1)生成,也可以是一個預先定義的掩碼,類似於 [7] 中的方法。研究者假定大條目遮罩 M^H 在設計上是稀疏的,且其非零條目數是有界的 。
。
如圖 2 所示,本文方法是基於一個重要的觀察結果。屏蔽注意力 M^C⊙A 可以分解成三個非零矩陣,每個矩陣的大小是原始注意力矩陣的一半。完全位於對角線下方的 A_21 塊是未屏蔽注意力。因此,我們可以使用演算法 2 近似來計算其行和。
圖2 中顯示的兩個對角線區塊 #和
#和 是因果注意力,其大小只有原來的一半。為了處理這些因果關係,研究者採用遞歸方法,將它們進一步分割成更小的區塊,並重複這個過程。演算法 4 中給出了這一過程的偽代碼。
是因果注意力,其大小只有原來的一半。為了處理這些因果關係,研究者採用遞歸方法,將它們進一步分割成更小的區塊,並重複這個過程。演算法 4 中給出了這一過程的偽代碼。

實驗及結果
#研究者透過擴展現有大語言模型來處理long range 序列,進而對演算法進行基準測試。所有實驗都在單一 40GB 的 A100 GPU 上運行,並使用 FlashAttention 2 進行精確的注意力計算。
為了保持原意不變,需要將內容改寫成中文,不需要出現原句子
研究者首先在两个预训练 LLM 上评估 HyperAttention,选择了实际应用中广泛使用的具有不同架构的两个模型:chatglm2-6b-32k 和 phi-1.5。
在操作中,他们通过替换为 HyperAttention 来 patch 最终的ℓ注意力层,其中ℓ的数量可以从 0 到每个 LLM 中所有注意力层的总数不等。请注意,两个模型中的注意力都需要因果掩码,并且递归地应用算法 4 直到输入序列长度 n 小于 4,096。对于所有序列长度,研究者将 bucket 大小 b 和采样列数 m 均设置为 256。他们从困惑度和加速度两个方面评估了这类 monkey patched 模型的性能。
同时研究者使用了一个长上下文基准数据集的集合 LongBench,它包含了 6 个不同的任务,即单 / 多文档问答、摘要、小样本学习、合成任务和代码补全。他们选择了编码序列长度大于 32,768 的数据集的子集,并且如果长度超过 32,768,则进行剪枝。接着计算每个模型的困惑度,即下一个 token 预测的损失。为了突出长序列的可扩展性,研究者还计算所有注意力层的总加速,无论是由 HyperAttention 还是 FlashAttention 执行。
上图3显示的结果如下,即使chatglm2-6b-32k经过了HyperAttention的monkey patch,仍然显示出合理的困惑度。例如,替换了20层后,困惑度大约增加了1,并在达到24层之前继续缓慢增加。注意力层的运行时提升了大约50%。如果替换了所有层,困惑度将上升到12,并且运行速度提高了2.3倍。phi-1.5模型也表现出类似的情况,但随着HyperAttention数量的增加,困惑度会线性增长

此外,研究者还对 LongBench 数据集上的 monkey patched chatglm2-6b-32k 进行了性能评估,并计算了单/多文档问答、摘要、小样本学习、合成任务和代码补全等各自任务的评估分数。评估结果如下表 1 所示
虽然替换 HyperAttention 通常会导致性能下降,但他们观察到它的影响会基于手头任务发生变化。例如,摘要和代码补全相对于其他任务具有最强的稳健性。

显著的一点是,当半数注意力层(即 14 层)被 patch 之后,研究者证实了大多数任务的性能下降幅度不会超过 13%。尤其是摘要任务,其性能几乎保持不变,表明该任务对注意力机制中的部分修改具有最强的稳健性。当 n=32k 时,注意力层的计算速度提升了 1.5 倍。
单个自注意力层
研究者进一步探索了序列长度从 4,096 到 131,072 不等时,HyperAttention 的加速度。他们测量了当使用 FlashAttention 计算或通过 HyperAttention 加速时,前向和前向 后向操作的挂钟时间。此外还测量了有或没有因果掩码时的挂钟时间。所有输入 Q、K 和 V 的长度相同,维数固定为 d = 64,注意力头数量为 12。
他们在HyperAttention中选择与前文相同的参数。如图4所示,没有应用因果掩码时,HyperAttention的速度提升了54倍,而使用因果掩码后,速度提升了5.4倍。尽管因果掩码和非掩码的时间困惑度相同,但因果掩码的实际算法(算法1)需要额外的操作,例如分区Q、K和V、合并注意力输出,从而导致实际运行时的增加。当序列长度n增加时,加速度会更高
研究者认为,这些结果不仅适用于推理,还可以用于训练或微调LLM以适应更长的序列,这为自注意力的扩展开辟了新的可能

以上是全新近似注意力機制HyperAttention:對長上下文友善、LLM推理加速50%的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM
AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM經常使用“ AI-Ready勞動力”一詞,但是在供應鏈行業中確實意味著什麼? 供應鏈管理協會(ASCM)首席執行官安倍·埃什肯納齊(Abe Eshkenazi)表示,它表示能夠評論家的專業人員
 一家公司如何悄悄地努力改變AIApr 26, 2025 am 11:12 AM
一家公司如何悄悄地努力改變AIApr 26, 2025 am 11:12 AM分散的AI革命正在悄悄地獲得動力。 本週五在德克薩斯州奧斯汀,Bittensor最終遊戲峰會標誌著一個關鍵時刻,將分散的AI(DEAI)從理論轉變為實際應用。 與閃閃發光的廣告不同
 NVIDIA釋放NEMO微服務以簡化AI代理開發Apr 26, 2025 am 11:11 AM
NVIDIA釋放NEMO微服務以簡化AI代理開發Apr 26, 2025 am 11:11 AM企業AI面臨數據集成挑戰 企業AI的應用面臨一項重大挑戰:構建能夠通過持續學習業務數據來保持準確性和實用性的系統。 NeMo微服務通過創建Nvidia所描述的“數據飛輪”來解決這個問題,允許AI系統通過持續接觸企業信息和用戶互動來保持相關性。 這個新推出的工具包包含五個關鍵微服務: NeMo Customizer 處理大型語言模型的微調,具有更高的訓練吞吐量。 NeMo Evaluator 提供針對自定義基準的AI模型簡化評估。 NeMo Guardrails 實施安全控制,以保持合規性和適當的
 AI為藝術與設計的未來描繪了一幅新圖片Apr 26, 2025 am 11:10 AM
AI為藝術與設計的未來描繪了一幅新圖片Apr 26, 2025 am 11:10 AMAI:藝術與設計的未來畫卷 人工智能(AI)正以前所未有的方式改變藝術與設計領域,其影響已不僅限於業餘愛好者,更深刻地波及專業人士。 AI生成的藝術作品和設計方案正在迅速取代傳統的素材圖片和許多交易性設計活動中的設計師,例如廣告、社交媒體圖片生成和網頁設計。 然而,專業藝術家和設計師也發現AI的實用價值。他們將AI作為輔助工具,探索新的美學可能性,融合不同的風格,創造新穎的視覺效果。 AI幫助藝術家和設計師自動化重複性任務,提出不同的設計元素並提供創意輸入。 AI支持風格遷移,即將一種圖像的風格應用
 Zoom如何徹底改變與Agent AI的合作:從會議到里程碑Apr 26, 2025 am 11:09 AM
Zoom如何徹底改變與Agent AI的合作:從會議到里程碑Apr 26, 2025 am 11:09 AMZoom最初以其視頻會議平台而聞名,它通過創新使用Agentic AI來引領工作場所革命。 最近與Zoom的CTO XD黃的對話揭示了該公司雄心勃勃的願景。 定義代理AI 黃d
 對大學的存在威脅Apr 26, 2025 am 11:08 AM
對大學的存在威脅Apr 26, 2025 am 11:08 AMAI會徹底改變教育嗎? 這個問題是促使教育者和利益相關者的認真反思。 AI融入教育既提出了機遇和挑戰。 正如科技Edvocate的馬修·林奇(Matthew Lynch)所指出的那樣
 原型:美國科學家正在國外尋找工作Apr 26, 2025 am 11:07 AM
原型:美國科學家正在國外尋找工作Apr 26, 2025 am 11:07 AM美國科學研究和技術發展或將面臨挑戰,這或許是由於預算削減導致的。據《自然》雜誌報導,2025年1月至3月期間,美國科學家申請海外工作的數量比2024年同期增加了32%。此前一項民意調查顯示,75%的受訪研究人員正在考慮前往歐洲和加拿大尋找工作。 過去幾個月,數百項NIH和NSF的撥款被終止,NIH今年的新撥款減少了約23億美元,下降幅度接近三分之一。洩露的預算提案顯示,特朗普政府正在考慮大幅削減科學機構的預算,削減幅度可能高達50%。 基礎研究領域的動盪也影響了美國的一大優勢:吸引海外人才。 35
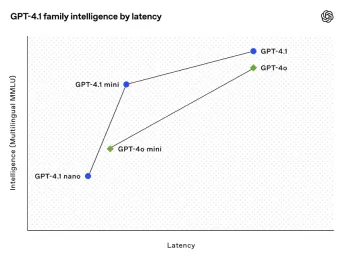 所有有關打開AI最新的GPT 4.1家庭的信息 - 分析VidhyaApr 26, 2025 am 10:19 AM
所有有關打開AI最新的GPT 4.1家庭的信息 - 分析VidhyaApr 26, 2025 am 10:19 AMOpenai推出了強大的GPT-4.1系列:一個專為現實世界應用設計的三種高級語言模型家族。 這種巨大的飛躍提供了更快的響應時間,增強的理解和大幅降低了成本


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

SublimeText3漢化版
中文版,非常好用

記事本++7.3.1
好用且免費的程式碼編輯器

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

SAP NetWeaver Server Adapter for Eclipse
將Eclipse與SAP NetWeaver應用伺服器整合。






