
基於時間序列的異常檢測問題,需要具體程式碼範例
時間序列資料是在時間上按照一定的順序記錄的數據,例如股票價格、氣溫變化、交通流量等。在實際應用中,對於時間序列資料的異常檢測具有重要的意義。異常值可以是與正常數據不一致的極端值、雜訊、錯誤數據,或是某種特定情況下的突發事件。異常檢測能夠幫助我們發現這些異常情況,從而採取相應的措施。
針對時間序列的異常檢測問題,常用的方法有很多,包括統計方法、機器學習方法和深度學習方法。本文將介紹兩種基於統計方法和機器學習方法的時間序列異常檢測演算法,並提供相應的程式碼範例。
一、基於統計方法的異常檢測演算法
1.1 均值-方差法
均值-方差法是最簡單的異常檢測方法之一。其基本想法是根據時間序列資料的平均值和變異數來判斷是否異常。若資料點與平均值的偏離程度大於一定的閾值(例如3倍標準差),則判斷為異常。
以下是使用Python實現均值-方差法進行時間序列異常檢測的程式碼範例:
import numpy as np
def detect_outliers_mean_std(data, threshold=3):
mean = np.mean(data)
std = np.std(data)
outliers = []
for i in range(len(data)):
if abs(data[i] - mean) > threshold * std:
outliers.append(i)
return outliers
# 示例数据
data = [1, 2, 3, 4, 5, 20, 6, 7, 8, 9]
# 检测异常值
outliers = detect_outliers_mean_std(data)
print("异常数据索引:", outliers)運行結果:
異常資料索引:[5]
1.2 箱型圖法
箱型圖法是另一種常用的異常檢測方法。它是基於數據的四分位數(上下四分位數、中位數)來判斷異常值。根據中位數(Q2)以及上下四分位數(Q1、Q3),可以計算出上下邊界,如果資料點超出這個邊界,則判斷為異常。
以下是使用Python實現箱型圖法進行時間序列異常檢測的程式碼範例:
import numpy as np
import seaborn as sns
def detect_outliers_boxplot(data):
q1 = np.percentile(data, 25)
q3 = np.percentile(data, 75)
iqr = q3 - q1
outliers = []
for i in range(len(data)):
if data[i] < q1 - 1.5 * iqr or data[i] > q3 + 1.5 * iqr:
outliers.append(i)
return outliers
# 示例数据
data = [1, 2, 3, 4, 5, 20, 6, 7, 8, 9]
# 绘制箱型图
sns.boxplot(data=data)
# 检测异常值
outliers = detect_outliers_boxplot(data)
print("异常数据索引:", outliers)運行結果:
異常資料索引:[5]
二、基於機器學習方法的異常檢測演算法
2.1 孤立森林演算法
#孤立森林演算法是一種基於無監督學習的異常檢測方法。它利用決策樹的分割方法來判斷資料點的異常程度。孤立森林演算法假設異常點在特徵空間上具有更低的密度,因此在建立決策樹時,異常點的路徑長度將更短。
以下是使用Python實作孤立森林演算法進行時間序列異常檢測的程式碼範例:
from sklearn.ensemble import IsolationForest
def detect_outliers_isolation_forest(data):
model = IsolationForest(contamination=0.1, random_state=0)
model.fit(data.reshape(-1, 1))
outliers = model.predict(data.reshape(-1, 1))
return np.where(outliers == -1)[0]
# 示例数据
data = [1, 2, 3, 4, 5, 20, 6, 7, 8, 9]
# 检测异常值
outliers = detect_outliers_isolation_forest(data)
print("异常数据索引:", outliers)運行結果:
異常資料索引:[5]
2.2 時間序列分解法
時間序列分解法是一種基於傳統統計方法的異常檢測方法,它將時間序列資料分解成趨勢、季節性和殘差三個部分,透過分析殘差來判斷異常點。
以下是使用Python實現時間序列分解法進行時間序列異常檢測的程式碼範例:
import statsmodels.api as sm
def detect_outliers_time_series(data):
decomposition = sm.tsa.seasonal_decompose(data, model='additive')
residuals = decomposition.resid
outliers = []
for i in range(len(residuals)):
if abs(residuals[i]) > 2 * np.std(residuals):
outliers.append(i)
return outliers
# 示例数据
data = [1, 7, 3, 4, 5, 20, 6, 7, 8, 9]
# 检测异常值
outliers = detect_outliers_time_series(data)
print("异常数据索引:", outliers)運行結果:
異常資料索引:[1, 5]
結語
基於時間序列的異常檢測問題是一個非常重要且實際的問題。本文介紹了兩種常用的異常檢測方法,包括基於統計方法的均值-方差法和箱型圖法,以及基於機器學習方法的孤立森林演算法和時間序列分解法。透過以上的程式碼範例,讀者可以了解如何使用Python實現這些演算法,並應用於實際的時間序列資料中進行異常檢測。希望本文對讀者對時間序列異常檢測有幫助。
以上是基於時間序列的異常檢測問題的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 如何使用C#编写时间序列预测算法Sep 19, 2023 pm 02:33 PM
如何使用C#编写时间序列预测算法Sep 19, 2023 pm 02:33 PM如何使用C#编写时间序列预测算法时间序列预测是一种通过分析过去的数据来预测未来数据趋势的方法。它在很多领域,如金融、销售和天气预报中有广泛的应用。在本文中,我们将介绍如何使用C#编写时间序列预测算法,并附上具体的代码示例。数据准备在进行时间序列预测之前,首先需要准备好数据。一般来说,时间序列数据应该具有足够的长度,并且是按照时间顺序排列的。你可以从数据库或者
 如何使用XGBoost和InluxDB进行时间序列预测Apr 04, 2023 pm 12:40 PM
如何使用XGBoost和InluxDB进行时间序列预测Apr 04, 2023 pm 12:40 PMXGBoost是一个流行的开源机器学习库,可用于解决各种预测问题。人们需要了解如何使用它与InfluxDB进行时间序列预测。 译者 | 李睿审校 | 孙淑娟XGBoost是一个开源的机器学习库,它实现了优化的分布式梯度增强算法。XGBoost使用并行处理实现快速性能,很好地处理缺失值,在小型数据集上执行良好,并防止过拟合。所有这些优点使XGBoost成为回归问题(例如预测)的一种流行解决方案。预测是各种业务目标的关键任务,例如预测分析、预测维护、产品规划、预算等。许多预测或预测问题都涉及到时间序
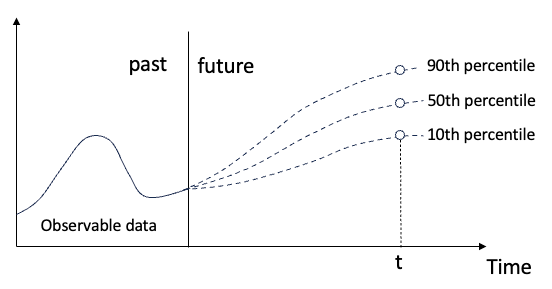 用于时间序列概率预测的分位数回归May 07, 2024 pm 05:04 PM
用于时间序列概率预测的分位数回归May 07, 2024 pm 05:04 PM不要改变原内容的意思,微调内容,重写内容,不要续写。“分位数回归满足这一需求,提供具有量化机会的预测区间。它是一种统计技术,用于模拟预测变量与响应变量之间的关系,特别是当响应变量的条件分布命令人感兴趣时。与传统的回归方法不同,分位数回归侧重于估计响应变量变量的条件量值,而不是条件均值。”图(A):分位数回归分位数回归概念分位数回归是估计⼀组回归变量X与被解释变量Y的分位数之间线性关系的建模⽅法。现有的回归模型实际上是研究被解释变量与解释变量之间关系的一种方法。他们关注解释变量与被解释变量之间的关
 时间序列预测+NLP大模型新作:为时序预测自动生成隐式PromptMar 18, 2024 am 09:20 AM
时间序列预测+NLP大模型新作:为时序预测自动生成隐式PromptMar 18, 2024 am 09:20 AM今天我想分享一个最新的研究工作,这项研究来自康涅狄格大学,提出了一种将时间序列数据与自然语言处理(NLP)大模型在隐空间上对齐的方法,以提高时间序列预测的效果。这一方法的关键在于利用隐空间提示(prompt)来增强时间序列预测的准确性。论文标题:S2IP-LLM:SemanticSpaceInformedPromptLearningwithLLMforTimeSeriesForecasting下载地址:https://arxiv.org/pdf/2403.05798v1.pdf1、问题背景大模型
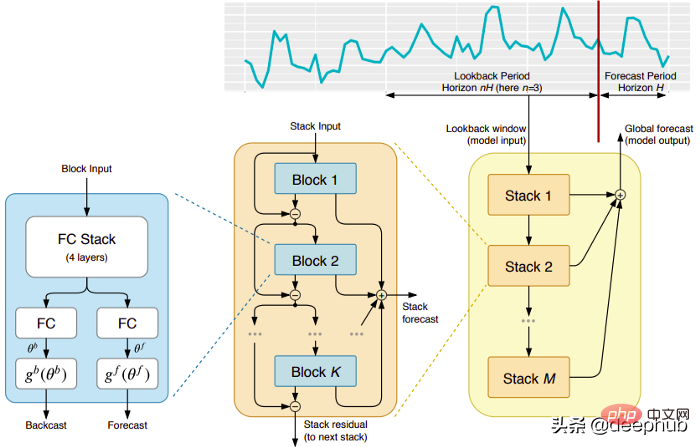 五个时间序列预测的深度学习模型对比总结May 05, 2023 pm 05:16 PM
五个时间序列预测的深度学习模型对比总结May 05, 2023 pm 05:16 PMMakridakisM-Competitions系列(分别称为M4和M5)分别在2018年和2020年举办(M6也在今年举办了)。对于那些不了解的人来说,m系列得比赛可以被认为是时间序列生态系统的一种现有状态的总结,为当前得预测的理论和实践提供了经验和客观的证据。2018年M4的结果表明,纯粹的“ML”方法在很大程度上胜过传统的统计方法,这在当时是出乎意料的。在两年后的M5[1]中,最的高分是仅具有“ML”方法。并且所有前50名基本上都是基于ML的(大部分是树型模型)。这场比赛看到了LightG
 如何用PHP实现异常检测与欺诈分析Jul 30, 2023 am 09:42 AM
如何用PHP实现异常检测与欺诈分析Jul 30, 2023 am 09:42 AM如何用PHP实现异常检测与欺诈分析摘要:随着电子商务的发展,欺诈成为一个不可忽视的问题。本文介绍了如何用PHP实现异常检测与欺诈分析。通过收集用户交易数据和行为数据,结合机器学习算法,在系统中实时监测和分析用户行为,识别潜在的欺诈行为,并采取相应措施应对。关键词:PHP、异常检测、欺诈分析、机器学习一、引言随着电子商务的快速发展,人们在互联网上进行交易的数量
 2022年十个用于时间序列分析的Python库推荐Apr 13, 2023 am 08:22 AM
2022年十个用于时间序列分析的Python库推荐Apr 13, 2023 am 08:22 AM时间序列是数据点的序列,通常由在一段时间间隔内进行的连续测量组成。时间序列分析是使用统计技术对时间序列数据进行建模和分析,以便从中提取有意义的信息并做出预测的过程。时间序列分析是一个强大的工具,可以用来从数据中提取有价值的信息,并对未来的事件做出预测。它可以用来识别趋势、季节模式和变量之间的其他关系。时间序列分析还可以用来预测未来的事件,如销售、需求或价格变动。如果你正在使用Python处理时间序列数据,那么有许多不同的库可以选择。所以在本文中,我们将整理Python中最流行处理时间序列的库。S
 Python中的ARMA模型详解Jun 10, 2023 pm 03:26 PM
Python中的ARMA模型详解Jun 10, 2023 pm 03:26 PMPython中的ARMA模型详解ARMA模型是统计学中一类重要的时间序列模型,它可以用于对时间序列数据的预测和分析。Python中提供了丰富的库和工具箱,可以方便地运用ARMA模型进行时间序列建模。本文将详细介绍Python中的ARMA模型。一、什么是ARMA模型ARMA模型是由自回归模型(AR模型)和移动平均模型(MA模型)组成的时间序列模型。其中,AR模


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

PhpStorm Mac 版本
最新(2018.2.1 )專業的PHP整合開發工具

Atom編輯器mac版下載
最受歡迎的的開源編輯器

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

Dreamweaver Mac版
視覺化網頁開發工具





