自己動手做過莫比烏斯帶嗎?


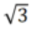 的縱橫比構造出來。例如,如果帶子長度為 1 厘米,它的寬度必須大於
的縱橫比構造出來。例如,如果帶子長度為 1 厘米,它的寬度必須大於 厘米。
厘米。 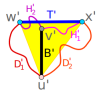
以上是製作莫比烏斯環,最少需要多長紙帶? 50年來的謎題被解開了的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 最新的最佳及時工程技術的年度彙編Apr 10, 2025 am 11:22 AM
最新的最佳及時工程技術的年度彙編Apr 10, 2025 am 11:22 AM對於那些可能是我專欄新手的人,我廣泛探討了AI的最新進展,包括體現AI,AI推理,AI中的高科技突破,及時的工程,AI培訓,AI,AI RE RE等主題
 歐洲的AI大陸行動計劃:Gigafactories,Data Labs和Green AIApr 10, 2025 am 11:21 AM
歐洲的AI大陸行動計劃:Gigafactories,Data Labs和Green AIApr 10, 2025 am 11:21 AM歐洲雄心勃勃的AI大陸行動計劃旨在將歐盟確立為人工智能的全球領導者。 一個關鍵要素是建立了AI Gigafactories網絡,每個網絡都有大約100,000個高級AI芯片 - 2倍的自動化合物的四倍
 微軟的直接代理商故事是否足以創造更多的粉絲?Apr 10, 2025 am 11:20 AM
微軟的直接代理商故事是否足以創造更多的粉絲?Apr 10, 2025 am 11:20 AM微軟對AI代理申請的統一方法:企業的明顯勝利 微軟最近公告的新AI代理能力清晰而統一的演講給人留下了深刻的印象。 與許多技術公告陷入困境不同
 向員工出售AI策略:Shopify首席執行官的宣言Apr 10, 2025 am 11:19 AM
向員工出售AI策略:Shopify首席執行官的宣言Apr 10, 2025 am 11:19 AMShopify首席執行官TobiLütke最近的備忘錄大膽地宣布AI對每位員工的基本期望是公司內部的重大文化轉變。 這不是短暫的趨勢。這是整合到P中的新操作範式
 IBM啟動具有完整AI集成的Z17大型機Apr 10, 2025 am 11:18 AM
IBM啟動具有完整AI集成的Z17大型機Apr 10, 2025 am 11:18 AMIBM的Z17大型機:集成AI用於增強業務運營 上個月,在IBM的紐約總部,我收到了Z17功能的預覽。 以Z16的成功為基礎(於2022年推出並證明持續的收入增長
 5 Chatgpt提示取決於別人並完全相信自己Apr 10, 2025 am 11:17 AM
5 Chatgpt提示取決於別人並完全相信自己Apr 10, 2025 am 11:17 AM解鎖不可動搖的信心,消除了對外部驗證的需求! 這五個CHATGPT提示將指導您完全自力更生和自我感知的變革轉變。 只需複制,粘貼和自定義包圍
 AI與您的思想危險相似Apr 10, 2025 am 11:16 AM
AI與您的思想危險相似Apr 10, 2025 am 11:16 AM人工智能安全與研究公司 Anthropic 最近的一項[研究]開始揭示這些複雜過程的真相,展現出一種令人不安地與我們自身認知領域相似的複雜性。自然智能和人工智能可能比我們想像的更相似。 窺探內部:Anthropic 可解釋性研究 Anthropic 進行的研究的新發現代表了機制可解釋性領域的重大進展,該領域旨在反向工程 AI 的內部計算——不僅僅觀察 AI 做了什麼,而是理解它在人工神經元層面如何做到這一點。 想像一下,試圖通過繪製當有人看到特定物體或思考特定想法時哪些神經元會放電來理解大腦。 A
 龍翼展示高通的邊緣動力Apr 10, 2025 am 11:14 AM
龍翼展示高通的邊緣動力Apr 10, 2025 am 11:14 AM高通的龍翼:企業和基礎設施的戰略飛躍 高通公司通過其新的Dragonwing品牌在全球範圍內積極擴展其範圍,以全球為目標。 這不僅僅是雷布蘭


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

SecLists
SecLists是最終安全測試人員的伙伴。它是一個包含各種類型清單的集合,這些清單在安全評估過程中經常使用,而且都在一個地方。 SecLists透過方便地提供安全測試人員可能需要的所有列表,幫助提高安全測試的效率和生產力。清單類型包括使用者名稱、密碼、URL、模糊測試有效載荷、敏感資料模式、Web shell等等。測試人員只需將此儲存庫拉到新的測試機上,他就可以存取所需的每種類型的清單。

SublimeText3 英文版
推薦:為Win版本,支援程式碼提示!

Dreamweaver CS6
視覺化網頁開發工具





