
在Python中,主要使用兩種搜尋演算法。其中,第一個是線性搜索,第二個是二分搜索。
這兩種技術主要用於從給定數組或給定列表中搜尋元素。在搜尋元素時,任何類型的演算法都可以遵循兩種方法。其中一種是遞歸方法,另一種是迭代方法。讓我們討論兩種方法中的兩種演算法並解決類似的問題。
線性搜尋
線性搜尋技術也稱為順序搜尋。 「順序搜尋」這個名稱的含義絕對是由該搜尋演算法遵循的過程來證明的。它是一種方法或技術,用於在 Python 中查找數組或列表中的元素。
它被認為是所有其他搜尋演算法中最簡單和最容易的。,這個演算法的唯一缺點是效率不高。這就是為什麼不經常使用線性搜尋的主要原因。
演算法
Step 1 - 它僅透過將所需元素與給定數組中存在的每個元素進行比較來按順序搜尋元素。
-
##步驟2 - 如果找到所需的元素,將基礎元素的索引或位置顯示給使用者。
- ##Step 3
- 如果陣列中不存在該元素,則會通知使用者未找到該元素。這樣,演算法就處理完了。
一般來說,線性搜尋演算法對於小於或等於100的小型陣列或小型列表來說比較合適且高效,因為它會檢查並比較每個元素。
- 如果所需的要素定位到倉庫的最後位置,會耗費更多的時間。
- # ###例### 在下面的範例中,我們將學習使用線性搜尋在記憶體中尋找元素的過程。
上述程式的輸出如下:
雷雷範例(遞迴)
在下面的範例中,我們將學習使用增量方法在陣列中進行線性搜尋的過程。
雷雷 ###輸出###上述程式的輸出如下:
雷雷二分查找
二分查找演算法與線性查找演算法相當不同。它遵循完全不同的過程來搜尋陣列中的元素。它通常只考慮陣列陣列。
如果陣列在某些情況下沒有排序,則對搜尋陣列進行排序,然後開始二分演算法的過程。一旦陣列被二分搜尋考慮演算法,它首先被排序,然後演算法被陣列分配。
演算法
##步驟1
- 對叢集進行排序是第一步。 ##Step 2- - 陣列排序後,陣列被視為兩半。一半是從排序數組的第一個元素到中間元素,後半部是從排序數組的中間元素之後的元素到最後一個元素。
-
##Step 3
- 將鍵元素(要搜尋的元素稱為鍵元素)與排序數組的中間元素進行比較。 -
Step 4
- 如果鍵元素小於或等於排序數組的中間元素,則後半部元素將進一步忽略,因為鍵元素小於中間元素。因此,該元素肯定必須出現在第一個元素和中間元素之間。 -
##Step 6 - 如果鍵元素大於中間元素,則忽略已排序數組的前半部分,並考慮從中間元素到最後一個元素的元素。
##Step 7 - 在這些元素中,再次將關鍵元素與減半數組的中間元素進行比較,並重複相同的過程。如果關鍵元素大於減半數組的中間元素,則忽略前半部。
第8步 - 如果关键元素小于或等于被分割数组的中间元素,则被分割数组的后半部分将被忽略。通过这种方式,元素将在数组的任意一半中进行搜索。
因此,与线性搜索相比,复杂度减少了一半或更多,因为有一半的元素将在第一步中被移除或不被考虑。二分搜索的最佳情况时间复杂度为“O(1)”。二分搜索的最坏情况时间复杂度为“O(logn)”。这就是二分搜索算法的工作原理。让我们考虑一个例子,并应用二分搜索算法来找出数组中的关键元素。
Example
In this example, we are going to learn about the process of searching an element in an array using Binary search in recursive approach.
def recursive_binary(arr, first, last, key_element):
if first <= last:
mid = (first + last) // 2
if arr[mid] == key_element:
return mid
elif arr[mid] > key_element:
return recursive_binary(arr, first, mid - 1, key_element)
elif arr[mid] < key_element:
return recursive_binary(arr, mid + 1, last, key_element)
else:
return -1
arr = [20, 40, 60, 80, 100]
key = 80
max_size = len(arr)
result = recursive_binary(arr, 0, max_size - 1, key)
if result != -1:
print("The element", key, "is present at index", (result), "in the position", (result + 1))
else:
print("The element is not present in the array")
Output
上述程序的输出如下:
The element 80 is found at the index 3 and in the position 4
Example
In this example, we are going to learn about the process of searching an element in an array using Binary search in iterative approach.
def iterative_binary(arr, last, key_element):
first = 0
mid = 0
while first <= last:
mid = (first + last) // 2
if arr[mid] < key_element:
first = mid + 1
elif arr[mid] > key_element:
last = mid - 1
else:
return mid
return -1
arr = [20, 40, 60, 80, 100]
key = 80
max_size = len(arr)
result = iterative_binary(arr, max_size - 1, key)
if result != -1:
print("The element", key, "is present at index", (result), "in the position", (result + 1))
else:
print("The element is not present in the array")
Output
上述程序的输出如下:
The element 80 is found at the index 3 and in the position 4
这是二分搜索算法的工作原理。根据时间复杂度的概念,我们可以肯定二分搜索算法比线性搜索算法更高效,时间复杂度在其中起着重要的作用。通过使用这种类型的算法,可以搜索数组中的元素。尽管用于解决问题的过程不同,但结果不会波动。这是使用多种算法检查输出一致性的一个优点。
以上是Python程式在數組中搜尋元素的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 PyCharm社区版支持的插件足够吗?Feb 20, 2024 pm 04:42 PM
PyCharm社区版支持的插件足够吗?Feb 20, 2024 pm 04:42 PMPyCharm社区版支持的插件足够吗?需要具体代码示例随着Python语言在软件开发领域的应用越来越广泛,PyCharm作为一款专业的Python集成开发环境(IDE),备受开发者青睐。PyCharm分为专业版和社区版两个版本,其中社区版是免费提供的,但其插件支持相对专业版有所限制。那么问题来了,PyCharm社区版支持的插件足够吗?本文将通过具体的代码示例
 PyCharm高级教程:利用PyInstaller将代码打包为EXE格式Feb 20, 2024 am 09:34 AM
PyCharm高级教程:利用PyInstaller将代码打包为EXE格式Feb 20, 2024 am 09:34 AMPyCharm是一款功能强大的Python集成开发环境,提供了丰富的功能和工具来帮助开发者提高效率。其中,PyInstaller是一个常用的工具,可以将Python代码打包为可执行文件(EXE格式),方便在没有Python环境的机器上运行。在本篇文章中,我们将介绍如何在PyCharm中使用PyInstaller将Python代码打包为EXE格式,并提供具体的
 Python元编程:赋予你编程超能力的工具Feb 19, 2024 pm 04:45 PM
Python元编程:赋予你编程超能力的工具Feb 19, 2024 pm 04:45 PMpython元编程是一种强大的技术,它允许你对Python语言本身进行操作,赋予你编程超能力。元编程可以通过使用元类和装饰器来实现。元类是一种特殊的类,它负责创建其他类。装饰器是一种函数,它可以修改另一个函数的行为。元编程的一个常见用途是创建自定义的类。例如,你可以创建一个元类,它可以生成具有特定属性和方法的类。元编程还可以用于修改类的方法行为。例如,你可以创建一个装饰器,它可以对函数的输入和输出进行验证。元编程是一项强大的技术,它可以让你做很多有趣和有用的事情。如果你想成为一名更强大的Pyth
 Python程序:从字符串的右侧修剪字符串Sep 08, 2023 pm 06:21 PM
Python程序:从字符串的右侧修剪字符串Sep 08, 2023 pm 06:21 PM在Python中,我们有一个预定义的函数rstrip()来删除右侧的字符。这意味着它将删除字符串右侧的空格。让我们举一个例子来理解如何从字符串的左侧修剪。在给定的字符串“WIRELESS”中移除右侧字符串LESS并将结果值得到为“WIRE”。在给定的字符串“kingdom”中,删除右侧的字符串dom,得到结果值为“king”。语法以下示例中使用的语法为−isspace()这是Python中预定义的方法,用于允许字符中的空白、换行符或空格。rstrip("parameterasastri
 Geany你是最后知道的!Feb 03, 2024 pm 09:24 PM
Geany你是最后知道的!Feb 03, 2024 pm 09:24 PM我们来了解一下吧:Geany是一个小巧的使用GTK+2开发的跨平台的开源集成开发环境,以GPL许可证分发源代码,是免费的自由软件。当前版本:1.31。该软件小巧、启动迅速,界面简洁,功能简单。它支持基本的语法高亮、代码自动完成、调用提示、插件扩展。支持文件类型:C,CPP,Java,Python,PHP,HTML,DocBook,Perl,LateX和Bash脚本。对于写多种语言的程序员来说,拥有Geany可以说是非常的方便了。知道了这么多,是不是迫不及待想要去尝试一下呢?下面让我们开始进行下载
 使用海龟绘制柱状图的Python程序Aug 20, 2023 pm 04:57 PM
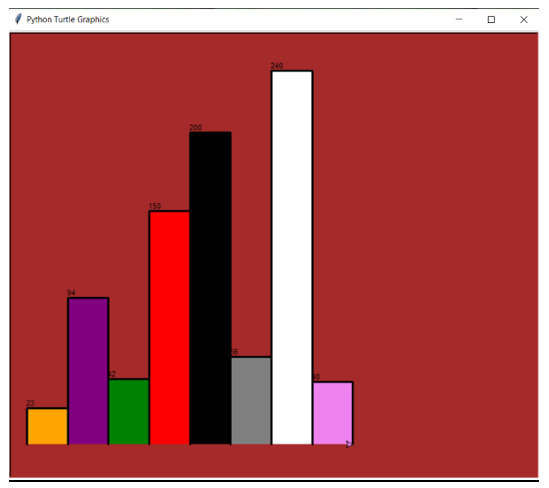
使用海龟绘制柱状图的Python程序Aug 20, 2023 pm 04:57 PM数据的图形表示提供了对数据复杂子结构的增强理解,帮助我们轻松解释隐藏的模式和趋势。想象一下,如果我们可以通过编程绘制类似的关系,那将是多么方便?Python提供了一个丰富的模块,专门用于执行此类操作,它被称为“turtle”。“turtle”模块是Python内置的库,允许我们在“turtle图形屏幕”上绘制图形。在本文中,我们将使用这个turtle模块创建一个条形图。理解Turtle模块Theturtlemoduleusesavirtualturtleobjecttocreategraphic
 Python程序以删除字典中的空值为例Sep 03, 2023 pm 04:45 PM
Python程序以删除字典中的空值为例Sep 03, 2023 pm 04:45 PM字典被称为集合数据类型。它们以键值对的形式存储数据。它们是有序的且可变的,即它们遵循特定的顺序并被索引。我们可以更改键的值,因此它是可操纵的或可更改的。字典不支持数据重复。每个键可以有多个与其关联的值,但单个值不能有多个键。我们可以使用字典来执行许多操作。整个机制取决于存储的值。在本文中,我们将讨论可用于从字典中删除“空值”的技术。在开始主要操作之前,我们必须对字典中的值处理有一个深入的了解。让我们快速浏览一下本文的概述。本文分为两部分-第1st部分将重点介绍“空值”的概念及其意义。在第2nd部
 Python程序提取网格匹配字符串Sep 09, 2023 pm 10:21 PM
Python程序提取网格匹配字符串Sep 09, 2023 pm 10:21 PM模式识别是一个重要的编程概念。它允许我们检索满足特定条件或匹配特定序列的特定数据。这一原理在语言和图像处理等各个领域都有帮助。字符串匹配帮助我们从大量数据中提取有意义的信息。在本文中,我们将讨论从给定字符串列表中提取网格匹配字符串的类似概念。网格匹配的重点是提取等长的“相似”字符串,我们来详细讨论这个问题。理解问题主要概念是提取遵循特定模式的相似字符串。网格字符串包含丢失的字符,并且应该提取与网格的隐藏模式匹配的那些字符串。让我们通过一个例子来理解这一点-输入输出场景Input:lis1=[&q


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

MantisBT
Mantis是一個易於部署的基於Web的缺陷追蹤工具,用於幫助產品缺陷追蹤。它需要PHP、MySQL和一個Web伺服器。請查看我們的演示和託管服務。

SublimeText3漢化版
中文版,非常好用

Dreamweaver CS6
視覺化網頁開發工具

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

DVWA
Damn Vulnerable Web App (DVWA) 是一個PHP/MySQL的Web應用程序,非常容易受到攻擊。它的主要目標是成為安全專業人員在合法環境中測試自己的技能和工具的輔助工具,幫助Web開發人員更好地理解保護網路應用程式的過程,並幫助教師/學生在課堂環境中教授/學習Web應用程式安全性。 DVWA的目標是透過簡單直接的介面練習一些最常見的Web漏洞,難度各不相同。請注意,該軟體中






