一個數位連線遊戲?
- PHPz轉載
- 2023-09-16 10:53:011490瀏覽
數位連接是一種邏輯謎題,涉及在網格中找到連接數字的路徑。
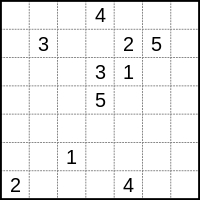
Numberlink謎題的一個簡單範例Numberlink謎題的解答
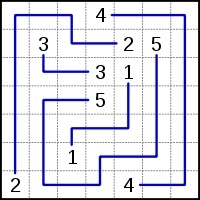
規則 -玩家必須用單一連續線(或路徑)將網格上的所有匹配數字配對。線條不能分叉或交叉,數字必須位於每條線的末端(即不在中間)。只有當問題具有唯一解並且網格中的所有單元格都填充時,才認為問題設計良好,儘管一些Numberlink設計師不規定這一點。
遊戲 - 考慮一個n×n的方塊陣列。其中一些方塊為空,有些方塊是實心的,有些非實心方塊被整數1、2、3、...標記。每個整數在棋盤上佔據兩個不同的方塊。玩家的任務是僅使用水平和垂直移動,透過簡單的路徑連接棋盤上每個整數的兩個出現。不允許兩條不同的路徑相交。任何路徑都不能包含任何實心方塊(任何路徑上都不允許出現實心方塊)。最後,所有非實心方塊必須由路徑填入。
演算法 - 要準備一個給定棋盤大小n×n的有效隨機謎題,我們首先在棋盤上產生隨機的簡單互不相交的路徑。如果有幾個孤立的方塊仍然在所有生成的路徑之外,將這些孤立的方塊標記為實心(禁止)。然後,我們將路徑的端點和實心方塊的清單作為謎題。
因此,我們先產生一個解答,然後從解答中解出謎題。路徑和實心方塊將n×n棋盤分割成若干部分。我們使用並查集資料結構來產生這個分割。資料結構處理棋盤上n^2個方塊的子集。
解釋
隨機在棋盤上找到方塊(i, j)和(k, l),使得:(a)(i, j)和(k , l)是彼此的鄰居,且(b)(i, j)和(k, l)都不屬於到目前為止產生的任何路徑。如果在整個棋盤上找不到這樣一枚方塊,則返回失敗 /* 在這裡,(i, j)和(k, l)是要建造的新路徑的前兩個方塊。 *
將包含(i, j)和(k, l)的兩個並查集樹合併。
重複下列步驟,直到目前路徑無法延伸:將(i, j)重新命名為(k, l)。隨機找到(i, j)的鄰居方塊(k, l),使得:(a)(k, l)不屬於到目前為止生成的任何路徑(包括當前路徑)(b)部分構建的當前路徑上( i, j)的唯一鄰居是(k, l)。
如果找不到這樣的鄰居方塊(k, l),則路徑無法進一步延伸,因此跳出循環
否則,將包含(i, j)和(k, l)的兩個並查集樹合併。
設定新路徑的起始方塊和終點方塊的標誌。
返回成功
#
| || || || || || || 4 | | || || || || || 3 || | | || || 2 || 2 || || || 3 | | || || || || X || || 1 | | || || 6 || || || 7 || 7 | | 5 || 4 || || X || || X || 1 | | || 5 || || 6 || || || |
輸出
上表的解###
| 4 || 4 || 4 || 4 || 4 || 4 || 4 | | 4 || 1 || 1 || 1 || 1 || 3 || 3 | | 4 || 1 || 2 || 2 || 1 || 1 || 3 | | 4 || 1 || 1 || 1 || X || 1 || 1 | | 4 || 4 || 6 || 1 || 1 || 7 || 7 | | 5 || 4 || 6 || X || 1 || X || 1 | | 5 || 5 || 6 || 6 || 1 || 1 || 1 |###範例###
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
struct _node *parent;
int rank;
int path_number;
int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
int i, j;
for (i=0;i<n;i++){
for (j=0;j<n;j++){
node *np;
np = (node *)malloc(sizeof(node));
np->rank = 0;
np->parent = NULL;
np->path_number = 0;
np->endpoint = 0;
arr[i][j] = np;
}
}
}
/*#############Input:a node Output:the set pointer of the set the node belongs to######描述### - 取得一個節點並傳回設定的指針。 */###
node *findset(node *n) {
if (n->parent != NULL)
n = n->parent;
return n;
}
void setunion(node *x, node *y) {
x = findset(x);
y = findset(y);
if (x->rank > y->rank)
y->parent = x;
else {
x->parent = y;
if(x->rank == y->rank)
y->rank++;
}
}
int neighbour(int n, node ***arr) {
int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
int k = rand()%(n*n);
while (ct < (n*n)) {
k %= (n*n);
i1 = k/n;
j1 = k%n;
if (arr[i1][j1]->path_number==0) {
int kk = rand()%4;
int cc = 0;
switch (kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 4: if(cc==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 5: if(cc==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 6: if(cc==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 7: if(cc==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
}
}
if(flag==1)
break;
ct++;
k++;
}
if(ct<n*n) {
k2= (i2*n)+j2;
return k*(n*n)+k2;
} else {
return -1;
}
}
int checkneigh(int k1, int k2, int n, node ***arr) {
int i= k2/n;
int j= k2%n;
int ii= k1/n;
int jj= k1%n;
int ct=0;
if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
ct++;
if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
ct++;
if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
ct++;
if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
ct++;
if(ct>1)
return 0;
else
return 1;
}
int valid_next(int k, int n, node ***arr) {
int i1, i2, j1, j2, a, b, kk, stat,ct=0;
int flag=0;
i1= k/n;
j1= k%n;
kk= rand()%4;
switch(kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 4: if(ct==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 5: if(ct==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 6: if(ct==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 7: if(ct==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
}
//printf("flag- %d</p><p>",flag);
if(flag==0)
return -1;
if(flag) {
//printf("value sent- %d</p><p>", i2*n + j2);
return (i2*n)+j2;
}
}
int addpath(node ***arr, int n, int ptno) {
int a,b,k1,k2;
int i1,j1,i2,j2;
k2= neighbour( n, arr);
if(k2==-1) //no valid pair found to start with
return 0;
k1= k2/(n*n);
k2= k2%(n*n);
//printf("%d %d</p><p>",k1,k2);
i1= k1/n;
j1= k1%n;
i2= k2/n;
j2= k2%n;
arr[i1][j1]->endpoint= 1;
arr[i2][j2]->path_number= ptno;
arr[i1][j1]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1, n2);
while(1) {
i1= i2;
j1= j2;
k1= (i1*n)+j1;
k2= valid_next(k1,n,arr);
if(k2==-1) {
arr[i1][j1]->endpoint= 1;
break;
}
i2=k2/n;
j2=k2%n;
arr[i2][j2]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1,n2);
}
return 1;
}
void printtable(node ***arr, int n) {
int i,j;
printf("Table to be solved:</p><p>");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->endpoint ==1){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else if(arr[i][j]->path_number==0)
printf("| X |");
else
printf("| |");
}
printf("</p><p>");
}
printf("</p><p></p><p>The solution to the above table:</p><p>");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->path_number != 0){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else
printf("| X |");
}
printf("</p><p>");
}
}
int main(void) {
srand((unsigned int) time (NULL));
int i, j;
int ct = 1;
int n = 7;
node*** pointers= (node ***)malloc(n*sizeof(node **));
for (i=0; i<n; i++)
pointers[i] = (node **)malloc(n*sizeof(node *));
initboard(pointers, n);
while(1) {
i = addpath(pointers, n, ct);
if (i==0) {
break;
} else {
ct++;
}
}
printtable(pointers,n);
return 0;
}###以上是一個數位連線遊戲?的詳細內容。更多資訊請關注PHP中文網其他相關文章!

