在C程式中,將下列內容翻譯為中文:3D中兩個平面的夾角
- 王林轉載
- 2023-08-25 16:41:10784瀏覽
這裡我們將看到如何計算三維空間中兩個平面之間的角度。平面是 P1 和 P2。 Pi 的方程式如下-
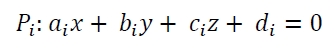
如果角度為“A”,則遵循此規則-
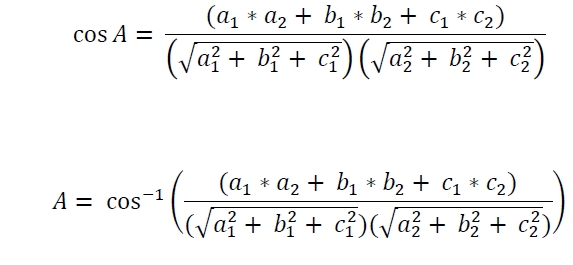
範例
#include <iostream>
#include <cmath>
using namespace std;
class Plane{
private:
double a, b, c, d;
public:
Plane(double a = 0, double b = 0, double c = 0, double d = 0){
this->a = a;
this->b = b;
this->c = c;
this->d = d;
}
double friend angle(Plane p1, Plane p2);
};
double angle(Plane p1, Plane p2){
double nume = (p1.a * p2.a) + (p1.b * p2.b) + (p1.c * p2.c);
double deno1 = (p1.a * p1.a) + (p1.b * p1.b) + (p1.c * p1.c);
double deno2 = (p2.a * p2.a) + (p2.b * p2.b) + (p2.c * p2.c);
return (180.0 / 3.14159) * acos(nume/ (sqrt(deno1) * sqrt(deno2)));
}
int main() {
Plane p1(2.0, 2.0, -3.0, -5.0), p2(3.0, -3.0, 5.0, -6.0);
cout << "Angle: " << angle(p1, p2) << " degree";
}輸出
Angle: 123.697 degree#
以上是在C程式中,將下列內容翻譯為中文:3D中兩個平面的夾角的詳細內容。更多資訊請關注PHP中文網其他相關文章!
陳述:
本文轉載於:tutorialspoint.com。如有侵權,請聯絡admin@php.cn刪除

