思考、思考、思考不停歇，思考樹ToT「軍訓」LLM

GPT 和 PaLM 等大型語言模型在處理數學、符號、常識和知識推理等任務時變得越來越熟練。也許令人驚訝的是，所有這些進展的基礎仍然是生成文本的原始自回歸機制。它逐一 token 地進行決策，並以從左到右的方式產生文字。這樣簡單的機制是否足以建構一個通用問題求解器的語言模型呢？如果不行，哪些問題將挑戰當前的範式，以及應該採用什麼樣的替代機制呢？

有關人類認知的文獻提供了一些線索來回答這些問題。關於「雙過程（dual process）」模型的研究表明，人們在進行決策時有兩種模式：一種是快速、自動、無意識的模式（System 1），另一種是緩慢、深思熟慮、有意識的模式（System 2）。這兩種模式以前與機器學習中使用的各種數學模型聯繫在一起。例如，對人類和其他動物的強化學習的研究探討了他們進行聯想式的「無模型」學習或更深思熟慮的「基於模型」的規劃的情況。語言模型的簡單聯想式token 級選擇也類似於“System 1”，因此可能受益於更深思熟慮的“System 2”規劃過程的增強，該過程保持並探索當前選擇的多種替代方案，而不僅僅是選擇一個。此外，它會評估其當前狀態，並積極地展望或回溯以進行更全局的決策。

為了設計這樣一個規劃過程，普林斯頓大學、 Google DeepMind 的研究者選擇先回顧一下人工智慧（和認知科學）的起源，汲取Newell、Shaw 和Simon 在上世紀50 年代探索的規劃過程的靈感。 Newell 和他的同事將問題解決描述為對組合式問題空間的搜索，這個空間被表示為一棵樹。因此，他們提出了適用於語言模型的思考樹（ToT）框架，用於通用問題求解。

#論文連結：https://arxiv.org/pdf/2305.10601 .pdf

專案地址：https://github.com/ysymyth/tree-of-thought-llm

如圖1 所示，現有的方法透過對連續語言序列進行取樣來解決問題，而ToT 則積極地維護一棵思考樹，其中每個思維都是一個連貫的語言序列，作為解決問題的中間步驟（表1）。

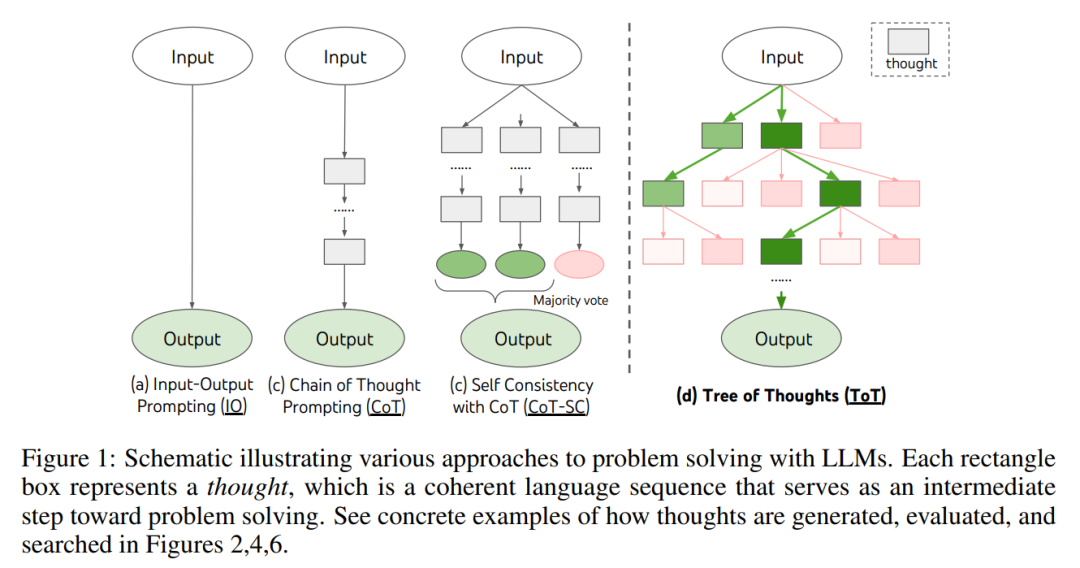
這樣一個高階語意單元讓LM 能夠透過深思熟慮的推理過程來自我評估不同中間思維對解決問題的進展貢獻（圖2、4、6）。透過 LM 的自我評估和深思熟慮來實現搜尋啟發式是一種新穎的方法，因為以前的搜尋啟發式要么是編程的，要么是學習得來的。

#最後，研究者將這種基於語言的生成和評估多樣化思維的能力與搜尋演算法相結合，例如廣度優先搜尋（BFS）或深度優先搜尋（DFS），這些演算法允許對思維樹進行系統性的探索，並具備展望和回溯功能。

在實驗階段，研究者設定了三項任務，即24 點遊戲、創意寫作和填字遊戲（表1），這些問題對現有的LM 推理方法來說頗具挑戰性，即使對GPT-4 來說也不例外。這些任務要求具備演繹、數學、常識、詞彙推理能力，以及融入系統性規劃或搜尋的方式。實驗結果表明，ToT 在這三個任務上取得了優越的成績，因為它具備足夠的通用性和靈活性，可以支持不同層次的思維、不同生成和評估思維的方式，以及適應不同問題性質的不同搜尋演算法。透過系統性的實驗消融分析，作者也探討了這些選擇如何影響模型效能，並討論了未來訓練和使用 LM 的方向。

思考樹：利用語言模型進行深思熟慮的問題求解

一個真正的問題求解過程涉及反複使用可用信息來啟動探索，進而揭示更多信息，直到最終發現實現解決方案的方法。 —— Newell 等

對人類問題求解的研究表明，人類透過搜尋一個組合式問題空間來解決問題。這可以看作一棵樹，其中節點表示部分解，分支對應修改它們的運算子。選擇哪個分支是由啟發式決定的，這些啟發式幫助導航問題空間並引導問題解決者朝著解決方案的方向前進。這個觀點突顯了使用語言模型來解決通用問題的現有方法的兩個關鍵缺點：1）局部上，它們不探索思考過程中的不同延續 —— 樹的分支。 2）全局上，它們不包括任何類型的規劃、展望或回溯來幫助評估這些不同的選擇 —— 這種啟發式引導的搜尋似乎是人類問題求解的特徵。

為了解決這些問題，作者引入了思維樹（ToT），這是一種讓語言模型能夠在思維路徑上探索多種推理方式的範式（圖1 (c )）。 ToT 將任何問題框架化為對樹的搜索，其中每個節點是一個狀態 s = [x, z_1・・・i ]，表示帶有輸入和迄今為止的思維序列的部分解。 ToT 的具體實例包括回答以下四個問題：

• 1. 如何將中間過程分解為思考步驟；
• ##2 . 如何從每個狀態生成潛在思維；
• 3. 如何啟發式地評估狀態；
• 4. 使用什麼搜尋演算法。

1. 思維分解。雖然 CoT 在沒有明確分解的情況下對思維進行連貫的取樣，但 ToT 利用問題屬性來設計和分解中間思維步驟。如表 1 所示，根據不同的問題，思考可以是幾個單字（填字遊戲），一個等式（24 點遊戲），或是一段寫作計畫（創意寫作）。一般來說，思維應該足夠“小（small）”，以便LM 能產生預期多樣化的樣本（如生成太“大（big）”而不連貫一本書），但思維又應該足夠“大”，以便LM 可以評估其解決問題的前景（例如，產生一個token 通常太小而無法評估）。

2. 思維產生器 G (p_θ， s, k)。給定樹狀態 s = [x, z_1・・・i]，該研究利用兩種策略來為下一步思維 step 產生 k 個候選對象。

3. 狀態評估器 V (p_θ， S)。給定不同狀態的邊界，狀態評估器評估它們在解決問題方面的進展，以確定哪些狀態應該繼續探索，以及以何種順序進行探索。雖然啟發式是解決搜尋問題的標準方法，但它們通常要么是編製的（例如 DeepBlue），要么是需要學習的（例如 AlphaGo）。本文提出第三種替代方法，透過使用語言來有意地推理狀態。在適用的情況下，這種深思熟慮的啟發式方法可能比程式規則更靈活，比學習模型更有效。

與思維生成器類似，考慮兩種策略來單獨或一起評估狀態：

• （1）獨立評估每個狀態
• （2）跨狀態投票

#這兩個策略，可以多次提示LM 來整合價值或投票結果，用時間、資源、成本換得更可靠、穩健的啟發式。

4. 搜尋演算法。最後，在 ToT 框架內，可以根據樹狀結構即插即用不同的搜尋演算法。本文探討了兩個相對簡單的搜尋演算法，並將更進階的演算法留作以後進行研究：

• （1）廣度優先搜尋（BFS）(演算法1 )
• （2）深度優先搜尋（DFS）(演算法2)

從概念上講，ToT 作為語言模型解決一般問題的方法有幾個好處：

• （1）通用性。 IO、CoT、CoT- sc 和自我細化可以看作 ToT 的特殊情況（即深度和廣度有限的樹；圖 1）；
• ##（2）模組化。基本的 LM 以及思考分解、生成、評估和搜尋過程都可以獨立變化；
• （3）適應性。可以適應不同的問題屬性、LM 能力和資源限制；
• （4）便捷性。無需額外的訓練，只需要一個預先訓練的 LM 就足夠了。

實驗結果

研究提出了三個任務，即便使用最先進的語言模型GPT-4，透過標準的IO prompting 或思維鏈（CoT）prompting 進行採樣，這些任務仍然具有挑戰性。

24 點數學遊戲 

#給定四個數字，玩家需要在限定的時間內使用這四個數字和基本數學運算符號（加號、減號、乘號、除號）來建立一個表達式，使其結果為24。例如，給定數字：4、6、8、2，一個可能的解法是：(8 ÷ (4 - 2)) × 6 = 24。

如表 2 所示，使用 IO、CoT 和 CoT-SC prompting 方法在任務上表現不佳，僅實現了 7.3%、4.0% 和 9.0% 的成功率。相比之下，b（breadth） = 1 的 ToT 已經實現了 45% 的成功率，而 b = 5 時則達到了 74%。他們還考慮了 IO/CoT 的 oracle 設置，透過使用 k 個樣本中的最佳值來計算成功率 (1 ≤ k ≤ 100)。

為了將IO/CoT（k 個最佳結果）與ToT 進行比較，研究者考慮在ToT 中計算每個任務中訪問的樹節點數量，其中b = 1・・・5，並將5 個成功率映射在圖3 (a) 中，將IO/CoT（k 個最佳結果）視為在賭博機中存取k 個節點。毫不奇怪，CoT 比 IO 更具擴展性，而最好的 100 個 CoT 樣本實現了 49% 的成功率，但仍遠遠不及在 ToT 中探索更多節點（b > 1）。

#下圖3 (b) 分解了CoT 和ToT 樣本在任務失敗時的情況。值得注意的是，大約 60% 的 CoT 樣本在產生第一步，相當於生成前三個單字 (例如 “4 9”) 後就已經失敗了。這讓直接從左到右解碼的問題更加凸顯了。

#創意寫作

研究者也發明了一個創意寫作任務，輸入4 個隨機句子，輸出一篇包含四段的連貫文章，每段分別以4 個輸入句子結尾。這樣的任務是開放式和探索性的，挑戰了創造性思考和高階規劃。

下圖5 (a) 顯示了GPT-4 在100 個任務中的平均分數，其中ToT (7.56) 比IO (6.19) 和CoT (6.93) 生成了更連貫的段落。雖然這樣的自動度量可能會有噪聲，但圖5 (b) 證實，人類在100 passage 對中有41 對更喜歡ToT 而不是CoT，而只有21 對更喜歡CoT 而不是ToT (其他38 對被發現“相似連貫”)。

最後，迭代優化演算法在該自然語言任務上取得了更好效果，IO 一致性得分從 6.19 提高到 7.67，ToT 一致性得分從 7.56 提高到了 7.91。研究者認為，這可視為 ToT 框架中思維生成的第三種方法，新思維可以從細化舊思維產生，而不是順序生成。

#迷你填字遊戲

#在《24 點數學遊戲》和創意寫作中，ToT 是比較淺顯的── 最多需要3 個思考步驟就能達到最終的輸出。研究者將探索 5×5 迷你填字遊戲作為自然語言的更困難一層的搜尋問題。同樣，這次的目標不僅僅是解決任務，因為一般填字遊戲可以透過專門的 NLP pipeline 輕鬆解決，該 pipeline 利用大規模檢索而不是 LM。相反，研究者的目標是探索語言模型作為一個通用問題求解器的極限，探索它自身的思維，並以嚴謹的推理作為啟發式來引導自己的探索。

如下表3 所示，IO 和CoT 提示方法表現不佳，單字層級的成功率低於16%，而ToT 顯著提高了所有指標，實現了60% 的單字等級成功率，在20 個遊戲中解決了4 個。考慮到 IO 和 CoT 缺乏嘗試不同線索、更改決策或回溯的機制，這樣的提升並不令人驚訝。

以上是思考、思考、思考不停歇，思考樹ToT「軍訓」LLM的詳細內容。更多資訊請關注PHP中文網其他相關文章！