Java資料結構之集合框架與常用演算法有哪些

1 集合框架

1.1 集合框架概念

Java 集合框架Java Collection Framework ，又稱為容器container ，是定義在java.util 套件下的一組介面interfaces和其實作類別classes 。

其主要表現為將多個元素 element 置於一個單元中，用於對這些元素進行快速、便捷的存儲 store 、檢索 retrieve 、管理 manipulate ，即平時我們俗稱的增刪改 CRUD 。

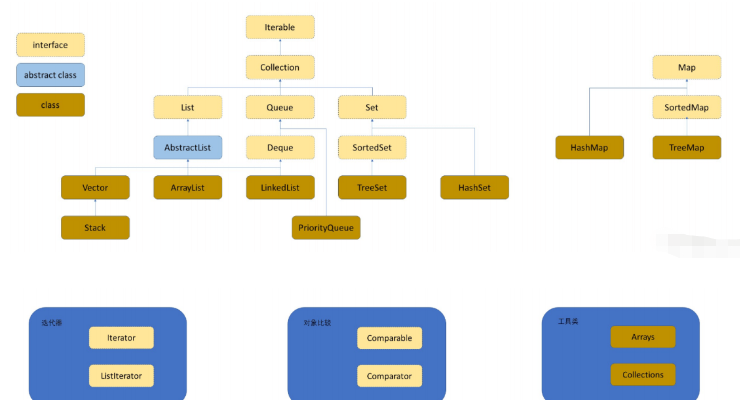
類別與介面總覽：

1.2 容器涉及的資料結構

Collection：是一個接口，包含了大部分容器常用的一些方法

List：是一個接口，規範了ArrayList 和LinkedList中要實現的方法

• ArrayList：實作了List接口，底層為動態類型順序表

• LinkedList：實作了List接口，底層為雙向鍊錶

Stack：底層是棧，堆疊是一種特殊的順序表

Queue：底層是隊列，隊列是一種特殊的順序表

Deque：是一個介面

Set：集合，是一個接口，裡面放置的是K模型

• HashSet：底層為雜湊桶，查詢的時間複雜度為O(1)

• TreeSet：底層為紅黑樹，查詢的時間複雜度為O( ),關於key有序的

Map：映射，裡面儲存的是K-V模型的鍵值對

• HashMap：底層為雜湊桶，查詢時間複雜度為O(1)

• #TreeMap：底層為紅黑樹，查詢的時間複雜度為O( )，關於key有序

2 演算法

2.1 演算法概念

演算法(Algorithm):就是定義良好的計算過程，他取一個或一組的值為輸入，並產生一個或一組值作為輸出。演算法是由一系列計算步驟組成的，其目的在於將輸入資料轉換為輸出結果。

2.2 演算法效率

演算法效率分析分為兩種：第一種是時間效率，第二種是空間效率。時間效率稱為時間複雜度，而空間效率被稱為空間複雜度。時間複雜度主要衡量的是一個演算法的運行速度，而空間複雜度主要衡量一個演算法所需的額外空間，在電腦發展的早期，電腦的儲存容量很小。所以對空間複雜度很在乎。隨著電腦產業的急速發展，電腦的儲存容量已經達到了相當高的水平。所以我們如今已經不需要再特別重視一個演算法的空間複雜度。

3 時間複雜度

3.1 時間複雜度概念

時間複雜度是計算機科學中的一個數學函數，表示演算法的運行時間，其定量描述了演算法的時間效率。在理論上無法計算一個演算法的執行時間，只有在將程式實際運行在計算機上之後才能得知其耗時。儘管每個演算法都可以進行上機測試，但這樣很繁瑣，因此才有了透過時間複雜度進行分析的方式。演算法的時間複雜度是基於其中語句執行次數的花費時間成正比例，時間複雜度取決於演算法中基本操作的執行次數。

3.2 大O的漸進表示法

// 请计算一下func1基本操作执行了多少次？
void func1(int N){
	int count = 0;
	for (int i = 0; i < N ; i++) {
		for (int j = 0; j < N ; j++) {
			count++;
		}
	}
	for (int k = 0; k < 2 * N ; k++) {
		count++;
	} 
	int M = 10;
	while ((M--) > 0) {
		count++;
	} 
	System.out.println(count);
}

Func1 執行的基本運算次數：F(N)=N^2 2*N 10

• #N = 10 F(N) = 130

• N = 100 F(N) = 10210

• N = 1000 F(N) = 1002010

實際中我們計算時間複雜度時，我們其實並不一定要計算精確的執行次數，而只需要大概執行次數，那麼這裡我們使用大O的漸進表示法。

大O符號（Big O notation）：是用來描述函數漸進式的數學符號

#3.3 推導大O階方法

• 用常數1取代運行時間中的所有加法常數。

• 在修改後的運行次數函數中，只保留最高階項。

• 如果最高階項存在且不是1，則移除與這個項目相乘的常數。得到的結果就是大O階。

使用大O的漸進表示法以後，Func1的時間複雜度為：O(n^2)

• N = 10 F (N) = 100

• N = 100 F(N) = 10000

• N = 1000 F(N) = 1000000

透過上述內容，我們可以看到大O漸進表示法排除了在結果上影響不大的項，從而簡潔明確地表示了執行次數。另外有些演算法的時間複雜度有最好、平均和最壞情況：

最壞情況：任意輸入規模的最大運行次數(上界)

平均情況：任意輸入規模的期望運行次數

最好情況：任意輸入規模的最小運行次數(下界)

例如：在一個長度為N數組中搜尋一個資料x

最好情況：1次找到

最壞情況：N次找到

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

4 空间复杂度

对于一个算法而言，空间复杂度表示它在执行期间所需的临时存储空间大小。空间复杂度的计算方式并非程序所占用的字节数量，因为这并没有太大的意义；实际上，空间复杂度的计算基于变量的数量。大O渐进表示法通常用来计算空间复杂度，其计算规则类似于实践复杂度的计算规则。

实例1:

// 计算bubbleSort的空间复杂度？
void bubbleSort(int[] array) {
	for (int end = array.length; end > 0; end--) {
		boolean sorted = true;
		for (int i = 1; i < end; i++) {
			if (array[i - 1] > array[i]) {
				Swap(array, i - 1, i);
				sorted = false;
			}
		} 
		if(sorted == true) {
		break;
		}
	}
}

实例2:

// 计算fibonacci的空间复杂度？
int[] fibonacci(int n) {
	long[] fibArray = new long[n + 1];
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n ; i++) {
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
	} 
	return fibArray;
}

实例3:

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {
	return N < 2 ? N : factorial(N-1)*N;
}

• 实例1使用了常数个额外空间，所以空间复杂度为 O(1)

• 实例2动态开辟了N个空间，空间复杂度为 O(N)

• 实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)

以上是Java資料結構之集合框架與常用演算法有哪些的詳細內容。更多資訊請關注PHP中文網其他相關文章！