Python中的@cache怎麼用

Python中的@cache有什麼妙用？

透過採用快取策略，可以將空間轉換為時間，進而提升電腦系統效能。快取在程式碼中的作用是優化程式碼的運行速度，儘管會增加記憶體佔用。

在Python的內建模組 functools 中，提供了高階函數 cache() 用於實作緩存，以裝飾器的方式使用： @cache。

@cache快取功能介紹

在cache的原始碼中，對cache的描述是：Simple lightweight unbounded cache. Sometimes called “memoize”. 翻譯成中文：簡單的輕量級無限制緩存。有時也被稱為「記憶化」。

def cache(user_function, /):
    'Simple lightweight unbounded cache.  Sometimes called "memoize".'
    return lru_cache(maxsize=None)(user_function)

cache() 的程式碼只有一行，呼叫了 lru_cache() 函數，傳入一個參數 maxsize=None。 lru_cache() 也是functools 模組中的函數，查看lru_cache() 的源碼，maxsize 的預設值是128，表示最大快取128個數據，如果數據超過了128個，則按LRU（最久未使用）刪除多的演算法數據。 cache()將maxsize設定成None，則 LRU 特性被停用且快取數量可以無限成長，所以稱為「unbounded cache」（無限制快取）。

lru_cache() 使用了 LRU（Least Recently Used）最久未使用演算法，這也是函數名稱中有 lru 三個字母的原因。最久未使用演算法的機制是，假設一個資料在最近一段時間沒有被存取到，那麼在將來它被存取的可能性也很小， LRU演算法選擇將最近最少使用的資料淘汰，保留那些經常被使用的數據。

cache() 是在Python3.9版本新增的，lru_cache() 是在Python3.2版本新增的， cache() 在lru_cache() 的基礎上取消了快取數量的限制，其實跟技術進步、硬體效能的大幅提升有關，cache() 和lru_cache() 只是同一個功能的不同版本。

lru_cache() 基本上是一個為函數提供快取功能的裝飾器，快取maxsize 群組傳入參數，下次以相同參數呼叫函數時直接返回上一次的結果，用以節約高開銷或高I/O函數的呼叫時間。

@cache的應用場景

快取的應用程式場景很廣泛，如靜態 Web 內容的緩存，可以直接在使用者存取靜態網頁的函數上加 @cache 裝飾器。

在某些遞歸的程式碼中，有重複傳入同一個參數執行函數程式碼的情況，使用快取可以避免重複計算，降低程式碼的時間複雜度。

接下來，我用斐波那契數列作為例子來說明 @cache 的作用，如果前面的內容你看完了還一知半解，相信看完例子你會茅塞頓開。

斐波那契數列是指這樣一個數列：1、1、2、3、5、8、13、21、34、… ，從第三個數開始，每個數都是前兩個數之和。大多數初學者都曾經編寫過斐波那契數列的程式碼，它的實作並不困難，在Python中，程式碼非常簡潔。如下：

def feibo(n):
    # 第0个数和第1个数为1
    a, b = 1, 1
    for _ in range(n):
        # 将b赋值给a,将a+b赋值给b,循环n次
        a, b = b, a+b
    return a

當然，斐波那契數列的程式碼實作方式有很多種（至少五、六種），本文為了說明@cache 的應用場景，用遞歸的方式來寫斐波那契數列的代碼。如下：

def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    # 根据斐波那契数列的定义，其他情况递归返回前两个数之和
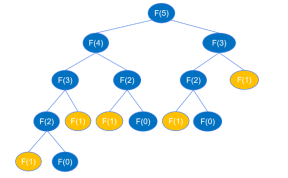
    return feibo_recur(n-1) + feibo_recur(n-2)

遞迴程式碼執行時會一直遞歸到feibo_recur(1)和feibo_recur(0)，如下圖所示（以求第6個數為例）。

求F(5)時要先求F(4)和F(3)，求F(4)時要先求F(3)和F( 2)，… 以此類推，遞歸的過程與二元樹深度優先遍歷的過程類似。已知高度為k 的二元樹最多可以有2k-1 個節點，根據上面遞歸調用的圖示，二叉樹的高度是n，節點最多為2n-1， 也就是遞歸呼叫函數的次數最多為2n-1 次，所以遞歸的時間複雜度為O(2^n) 。

時間複雜度為O(2^n)時，執行時間隨 n 的增大變化非常誇張，以下實際測試一下。

import time
for i in [10, 20, 30, 40]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

第10個斐波那契數: 89
n=10 Cost Time:  0.0
第20個斐波那契數: 10946
n=20 Cost Time:  0.0015988349914550781
第30個斐波那契數: 1346269
n=30 Cost Time:  0.170512914657512914657512916575129146575129112506221222012240 n=40 Cost Time:  20.90010976791382

從運行時間可以看出，在n 很小時，運行很快，隨著n 的增大，運行時間極速上升，尤其n 逐步增加到30和40時，運行時間變化得特別明顯。為了更清楚看出時間變化規律，再進一步進行測試。

for i in [41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

第41個斐波那契數: 267914296

n=41 Cost Time:  33.77224683761597

第42個斐波那契數: 433494437
n=42 Cost Time:  55.86398696899414
第43個斐波那契數: 701408733
n=43 Cost Time:  92.55108690261841

从上面的变化可以看到，时间是指数级增长的（大约按1.65的指数增长），这跟时间复杂度为 O(2^n) 相符。按照这个时间复杂度，假如要计算第50个斐波那契数列，差不多要等一个小时，非常不合理，也说明递归的实现方式运算量过大，存在明显的不足。如何解决这种不足，降低运算量呢？接下来看如何进行优化。

根据前面的分析，递归代码运算量大，是因为递归执行时会不断的计算 feibo_recur(n-1) 和 feibo_recur(n-2)，如示例图中，要得到 feibo_recur(5) ，feibo_recur(1) 调用了5次。随着 n 的增大，调用次数呈指数级增长，导致出现大量的重复操作，浪费了许多时间。

假如有一个地方将每个 n 的执行结果记录下来，当作“备忘录”，下次函数再接收到这个相同的参数时，直接从备忘录中获取结果，而不用去执行递归的过程，就可以避免这些重复调用。在 Python 中，可以创建一个字典或列表来当作“备忘录”使用。

temp = {}  # 创建一个空字典，用来记录第i个斐波那契数列的值
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    if n in temp:  # 如果temp字典中有n,则直接返回值,不调用递归代码
        return temp[n]
    else:
        # 如果字典中还没有第n个斐波那契数，则递归计算并保存到字典中
        temp[n] = feibo_recur_temp(n-1) + feibo_recur_temp(n-2)
        return temp[n]

上面的代码中，创建了一个空字典用于存放每个 n 的执行结果。每次调用函数，都先查看字典中是否有记录，如果有记录就直接返回，没有记录就递归执行并将结果记录到字典中，再从字典中返回结果。这里的递归其实都只执行了一次计算，并没有真正的递归，如第一次传入 n 等于 5，执行 feibo_recur_temp(5)，会递归执行 n 等于 4, 3, 2, 1, 0 的情况，每个 n 计算过一次后 temp 中都有了记录，后面都是直接到 temp 中取数相加。每个 n 都是从temp中取 n-1 和 n-2 的值来相加，执行一次计算，所以时间复杂度是 O(n) 。

下面看一下代码的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur_temp(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)
print(temp)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0
{2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986, 39: 102334155, 40: 165580141, 41: 267914296, 42: 433494437, 43: 701408733}

可以观察到，代码的运行时间已经减少到小数点后很多位了（时间过短，只显示了0.0）。然而，temp 字典存储了每个数字的斐波那契数，这需要使用额外的内存空间，以换取更高的时间效率。

上面的代码也可以用列表来当“备忘录”，代码如下。

temp = [1, 1]
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    if n < len(temp):
        return temp[n]
    else:
        # 第一次执行时，将结果保存到列表中，后续直接从列表中取
        temp.append(feibo_recur_temp(n-1) + feibo_recur_temp(n-2))
        return temp[n]

现在，已经剖析了递归代码重复执行带来的时间复杂度问题，也给出了优化时间复杂度的方法，让我们将注意力转回到本文介绍的 @cache 装饰器。@cache 装饰器的作用是将函数的执行结果缓存，在下次以相同参数调用函数时直接返回上一次的结果，与上面的优化方式完全一致。

所以，只需要在递归函数上加 @cache 装饰器，递归的重复执行就可以解决，时间复杂度就能从 O(2^n) 降为 O(n) 。代码如下：

from functools import cache
@cache
def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    return feibo_recur(n-1) + feibo_recur(n-2)

使用 @cache 装饰器，可以让代码更简洁优雅，并且让你专注于处理业务逻辑，而不需要自己实现缓存。下面看一下实际的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0

完美地解决了问题，所有运行时间都被精确到了小数点后数位（即使只显示 0.0），非常巧妙。若今后遇到类似情形，可以直接采用 @cache 实现缓存功能，通过“记忆化”处理。

补充：Python @cache装饰器

@cache和@lru_cache(maxsize=None)可以用来寄存函数对已处理参数的结果，以便遇到相同参数可以直接给出答案。前者无限制存储数量，而后者通过设定maxsize限制存储数量的上限。

例：

@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):
    print('开始计算a+b的值...')
    return a + b

可以用来做某些递归、动态规划。比如斐波那契数列的各项值从小到大输出。其实类似用数组保存前项的结果，都需要额外的空间。不过用装饰器可以省略额外空间代码，减少了出错的风险。

以上是Python中的@cache怎麼用的詳細內容。更多資訊請關注PHP中文網其他相關文章！