Java Bellman-Ford演算法原理及實作方法

一 點睛

如果遇到負權邊，則在沒有負環（迴路的權值總和為負）存在時，可以採用 Bellman-Ford 演算法求解最短路徑。這個演算法的優點在於它可以處理變權值為負的情況並且實現簡單，但它的缺點是時間複雜度過高。但是該演算法可以進行若干種最佳化，以提高效率。

Bellman-Ford 演算法與 Dijkstra 演算法類似，都是以鬆弛操作為基礎。 Dijkstra 演算法以貪心法選取未被處理的具有最小權值的節點，然後對其進行鬆弛操作；而 Bellman-Ford 演算法對所有邊都進行鬆弛操作，共 n-1 次。如果第 n 次操作仍然可以鬆弛，則必定存在一個負環，因為負環可以不斷地減少最短路徑的長度。節點數為 n，邊數為 m，則 Bellman-Ford 演算法最長的運行時間為 O(nm)。

二 演算法步驟

1 資料結構

因為需要利用邊進行鬆弛，因此採用邊集陣列儲存。每條邊都有三個域：兩個端點a和b，以及邊權w

2 鬆弛運算

對所有的邊j(a,b,w),如果dis[ e[j]b]>dis[e[j].a] e[j].w,則鬆弛，另dis[e[j]b]=dis[e[j].a] e[j] .w。其中，dis[v] 表示從源點到節點 v 的最短路徑長度。

3 重複鬆弛運算 n-1 次

4 負環判斷

再執行一次鬆弛運算，如果仍可鬆弛，則表示右負環。

三演算法實現

package graph.bellmanford;
 
import java.util.Scanner;
 
public class BellmanFord {
    static node e[] = new node[210];
    static int dis[] = new int[110];
    static int n;
    static int m;
    static int cnt = 0;
 
    static {
        for (int i = 0; i < e.length; i++) {
            e[i] = new node();
        }
    }
 
    static void add(int a, int b, int w) {
        e[cnt].a = a;
        e[cnt].b = b;
        e[cnt++].w = w;
    }
 
    static boolean bellman_ford(int u) { // 求源点 u 到其它顶点的最短路径长度，判负环
        for (int i = 0; i < dis.length; i++) {
            dis[i] = 0x3f;
        }
        dis[u] = 0;
        for (int i = 1; i < n; i++) { // 执行 n-1 次
            boolean flag = false;
            for (int j = 0; j < m; j++) // 边数 m 或 cnt
                if (dis[e[j].b] > dis[e[j].a] + e[j].w) {
                    dis[e[j].b] = dis[e[j].a] + e[j].w;
                    flag = true;
                }
            if (!flag)
                return false;
        }
        for (int j = 0; j < m; j++) // 再执行 1 次，还能松弛说明有环
            if (dis[e[j].b] > dis[e[j].a] + e[j].w)
                return true;
        return false;
    }
 
 
    static void print() { // 输出源点到其它节点的最短距离
        System.out.println("最短距离：");
        for (int i = 1; i <= n; i++)
            System.out.print(dis[i] + " ");
        System.out.println();
    }
 
    public static void main(String[] args) {
        int a, b, w;
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        for (int i = 0; i < m; i++) {
            a = scanner.nextInt();
            b = scanner.nextInt();
            w = scanner.nextInt();
            add(a, b, w);
        }
        if (bellman_ford(1)) // 判断负环
            System.out.println("有负环！");
        else
            print();
    }
}
 
class node {
    int a;
    int b;
    int w;
}

四 測試

1 沒有負環的測試

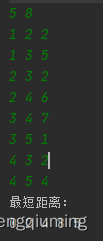
2 有負環的測試

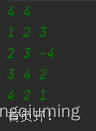
以上是Java Bellman-Ford演算法原理及實作方法的詳細內容。更多資訊請關注PHP中文網其他相關文章！