如何利用Python實現遺傳演算法解決旅行商問題（TSP）？
- WBOY轉載
- 2023-05-08 19:46:182467瀏覽
TSP問題
那麼在開始之前的話，咱們來仔細描述一下這個TSP問題。這個打過數模，或是接觸過智慧優化或機器學習的朋友應該都知道，當然為了本文的受眾普適性，咱們在這裡盡可能去完善一點，說清楚，這樣便於咱們去實際解決問題。
那麼這個問題的其實簡單，是這樣子的：
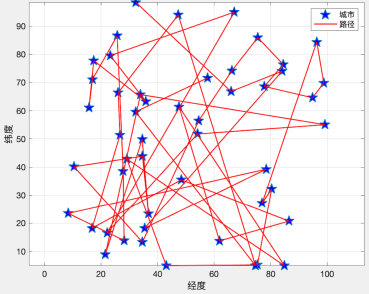
#在我們的N維平面是，咱們今天的話是拿這個二維平面來的，在這個平面上有很多個城市，城市之間是彼此聯通的，我們現在要找出一條最短的路徑可以將全部城市都走完。例如我們有城市A，B，C，D，E。現在知道了城市間的座標，也就是相當於知道了城市之間的距離，那麼現在找到一個順序，能夠使得走完A，B，C，D，E所有城市的路徑和最短。例如計算完之後可能是B－－＞Ａ－－＞Ｃ－－＞Ｅ－－＞Ｄ。換句話說要找到這個順序。
枚舉
首先要解決這個問題的話，其實方案有很多，說變白了，咱們就是要找到一個順序，能夠讓路徑之和最小，那麼最容易想到的自然就是枚舉，例如讓Ａ先走然後看距離Ａ最近的假設是Ｂ，那麼就走Ｂ，然後從Ｂ走。當然這個是局部貪心策略，很容易走到局部最優，那麼這個時候我們可以考慮ＤＰ，也就是說依然假設從Ａ開始，然後確保2個城市最短，3個城市最短，4個5個。最後在假設從B開始同理。或直接 列舉全部情況，計算距離。但無論如何，隨著城市數量的上升，他們的複雜度都會增加，所以這個時候我們就要想辦法讓計算能不能發揮一下咱們人類的專長了。我稱之為「瞎蒙」。
智慧演算法
現在我們來聊聊這個智慧演算法，以及為什麼要用玩意，剛剛咱們說了前面的方案對於大量的資料運算量會很大，也看不見得編寫簡單。那麼這個時候，首先單單對於TSP問題來說，我們要的就是一個序列，一個不會重複的序列。那麼這個時候，有什麼一個更簡單的方案，而且在資料夠大的情況下，我們也看不見得需要一個完全精準，完全最小的解，只要接近就好。那麼這個時候，採用傳統的那些演算法的話，一就是一，他只會按照我們的規則去計算，而且我們也確實不知道標準答案是什麼，對傳統演算法也比較難去設定一個閾值去停止運算。但是對我們人來說，有一種東西叫做“運氣”，有的人運氣賊好，可能一發入魂，一下子就懵出了答案。那我們的智慧演算法其實就是有點類似「蒙」。但是人家蒙是講究技巧的，例如經驗告訴我們，三長一短選最短，透過這個技巧可以去蒙一下答案，或者找男盆友的時候像博主一樣帥氣的男孩紙，只要一張40系（30也可以）顯示卡就可以輕鬆帶走一樣。蒙是要技巧的，我們管這個叫做策略。
策略
那麼我們剛剛說的這個技巧，這個蒙的技巧。在智慧演算法裡面，這個蒙，就是我們的一種策略。我們要怎麼去蒙才能讓我們的解更合理。那麼這個時候，就開始百花齊放了，這裡我就不念經了，我們拿最金典的兩個演算法為例子，一個是遺傳演算法，一個是粒子群演算法（PSO）。為例子，他們就是採用了一種策略去蒙，例如遺傳演算法，透過模擬物競天擇，一開始先隨機蒙出一堆解，一堆序列，然後按照咱們的這個物競天擇的策略出篩選這些解，然後透過這些解再去蒙出新的、更好的解。如此往復，之後蒙出不錯的解。粒子群也是類似的，這些部分咱們用的時候再詳細說明。
演算法
現在咱們已經知道了這個策略，那麼演算法是啥，其實就是實現這些策略的步驟啊，就是咱們的程式碼，咱們的循環，資料結構。我們要去實現剛剛說的例如物競天擇，例如咱們TSP，如何隨機產生一堆解。
資料範例
ok,到這裡咱們已經說完了，基本的一些概念，那麼這個時候的話，咱們來看看咱們如何表示這個TSP的問題，這個其實很簡單，咱們這邊的話就簡單的準備一個測試數據，我們這裡假設有14個城市，那麼我們的這些城市的數據如下：
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))我們後面都用這組數據進行測試，現在在上面已經有14個城市了。
那麼接下來我們開始我們的解決方案
遺傳演算法
ok,那麼我們來說一說咱們的這個遺傳演算法是怎麼一回事，之後的話，咱們用這個來解決這個TSP問題。
那麼現在的話，我們來看看我們的遺傳演算法是怎麼蒙的。
算法流程
遗传算法其实是在用计算机模拟我们的物种进化。其实更加通俗的说法是筛选，这个就和我们袁老爷爷种植水稻一样。有些个体发育良好，有些个体发育不好，那么我就先筛选出发育好的，然后让他们去繁衍后代，然后再筛选，最后得到高产水稻。其实也和我们社会一样，不努力就木有女朋友就不能保留自己的基因，然后剩下的人就是那些优秀的人和富二代的基因，这就是现实呀。所以得好好学习，天天向上！
那么回到主题，我们的遗传算法就是在模拟这一个过程，模拟一个物竞天择的过程。
所以在我们的算法里面也是分为几大块
繁殖
首先我们的种群需要先繁殖。这样才能不断产生优良基于，那么对应我们的算法，假设我们需要求取
Y = np.sin(10 * x) * x + np.cos(2 * x) * x
的最大值（在一个范围内）那么我们的个体就是一组（X1）的解。好的个体就会被保留，不好的就会被pass，选择标准就是我们的函数 Y 。那么问题来了如何模拟这个过程？我们都知道在繁殖后代的时候我们是通过DNA来保留我们的基因信息，在这个过程当中，父母的DNA交互，并且在这个过程当中会产生变异，这样一来，父母双方的优秀基于会被保存，并且产生的变异有可能诞生更加优秀的后代。
所以接下来我们需要模拟我们的ＤＮＡ，进行交叉和变异。
交叉
这个交叉过程和我们的生物其实很像，当然我们在我们的计算机里面对于数字我们可以将其转化为二进制，当做我们的DNA
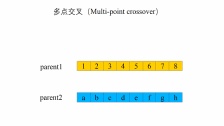
交叉的方式有很多，我们这边选择这一个，进行交叉。
变异
那这个在我们这里就更加简单了
我们只需要在交叉之后，再随机选择几个位置进行改变值就可以了。当然变异的概率是很小的，并且是随机的，这一点要注意。并且由于变异是随机的，所以不排除生成比原来还更加糟糕的个体。
选择
最后我们按照一定的规则去筛选这个些个体就可以了，然后淘汰原来的个体。那么在我们的计算机里面是使用了两个东西，首先我们要把原来二进制的玩意，给转化为我们原来的十进制然后带入我们的函数运算，然后保存起来，之后再每一轮统一筛选一下就好了。
逆转
这个咋说呢，说好听点叫逆转，难听点就算，对于一些新的生成的不好的解，我们是要舍弃的。
代码
那么这部分用代码描述的话就是这样的：
import numpy as np
import matplotlib.pyplot as plt
Population_Size = 100
Iteration_Number = 200
Cross_Rate = 0.8
Mutation_Rate = 0.003
Dna_Size = 10
X_Range=[0,5]
def F(x):
'''
目标函数，需要被优化的函数
:param x:
:return:
'''
return np.sin(10 * x) * x + np.cos(2 * x) * x
def CrossOver(Parent,PopSpace):
'''
交叉DNA，我们直接在种群里面选择一个交配
然后就生出孩子了
:param parent:
:param PopSpace:
:return:
'''
if(np.random.rand()) < Cross_Rate:
cross_place = np.random.randint(0, 2, size=Dna_Size).astype(np.bool)
cross_one = np.random.randint(0, Population_Size, size=1) #选择一位男/女士交配
Parent[cross_place] = PopSpace[cross_one,cross_place]
return Parent
def Mutate(Child):
'''
变异
:param Child:
:return:
'''
for point in range(Dna_Size):
if np.random.rand() < Mutation_Rate:
Child[point] = 1 if Child[point] == 0 else 0
return Child
def TranslateDNA(PopSpace):
'''
把二进制转化为十进制方便计算
:param PopSpace:
:return:
'''
return PopSpace.dot(2 ** np.arange(Dna_Size)[::-1]) / float(2 ** Dna_Size - 1) * X_Range[1]
def Fitness(pred):
'''
这个其实是对我们得到的F(x)进行换算，其实就是选择的时候
的概率，我们需要处理负数，因为概率不能为负数呀
pred 这是一个二维矩阵
:param pred:
:return:
'''
return pred + 1e-3 - np.min(pred)
def Select(PopSpace,Fitness):
'''
选择
:param PopSpace:
:param Fitness:
:return:
'''
'''
这里注意的是，我们先按照权重去选择我们的优良个体，所以我们这里选择的时候允许重复的元素出现
之后我们就可以去掉这些重复的元素，这样才能实现保留良种去除劣种。100--》70（假设有30个重复）
如果不允许重复的话，那你相当于没有筛选
'''
Better_Ones = np.random.choice(np.arange(Population_Size), size=Population_Size, replace=True,
p=Fitness / Fitness.sum())
# np.unique(Better_Ones) #这个是我后面加的
return PopSpace[Better_Ones]
if __name__ == '__main__':
PopSpace = np.random.randint(2, size=(Population_Size, Dna_Size)) # initialize the PopSpace DNA
plt.ion()
x = np.linspace(X_Range, 200)
# plt.plot(x, F(x))
plt.xticks([0,10])
plt.yticks([0,10])
for _ in range(Iteration_Number):
F_values = F(TranslateDNA(PopSpace))
# something about plotting
if 'sca' in globals():
sca.remove()
sca = plt.scatter(TranslateDNA(PopSpace), F_values, s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.05)
# GA part (evolution)
fitness = Fitness(F_values)
print("Most fitted DNA: ", PopSpace[np.argmax(fitness)])
PopSpace = Select(PopSpace, fitness)
PopSpace_copy = PopSpace.copy()
for parent in PopSpace:
child = CrossOver(parent, PopSpace_copy)
child = Mutate(child)
parent[:] = child
plt.ioff()
plt.show()这个代码是以前写的，逆转没有写上（下面的有）
TSP遗传算法
ok,刚刚的例子是拿的解方程，也就是说是一个连续问题吧，当然那个连续处理的话并不是很好，只是一个演示。那么我们这个的话其实类似的。首先我们的ＤＮＡ，是城市的路径，也就是A-B-C-D等等，当然我们用下标表示城市。
种群表示
首先我们确定了使用城市的序号作为我们的个体DNA，例如咱们种群大小为100，有ＡＢＣＤ四个城市，那么他就是这样的，我们先随机生成种群，长这个样：
1 2 3 4
2 3 4 5
3 2 1 4
...
那个1,2,3,4是ABCD的序号。
交叉与变异
这里面的话，值得一提的就是，由于暂定城市需要是不能重复的，且必须是完整的，所以如果像刚刚那样进行交叉或者变异的话，那么实际上会出点问题，我们不允许出现重复，且必须完整，对于我们的DNA，也就是咱们瞎蒙的个体。
代码
由于咱们每一步在代码里面都有注释，所以的话咱们在这里就不再进行复述了。
from math import floor
import numpy as np
import matplotlib.pyplot as plt
class Gena_TSP(object):
"""
使用遗传算法解决TSP问题
"""
def __init__(self, data, maxgen=200,
size_pop=200, cross_prob=0.9,
pmuta_prob=0.01, select_prob=0.8
):
self.maxgen = maxgen # 最大迭代次数
self.size_pop = size_pop # 群体个数，（一次性瞎蒙多少个解）
self.cross_prob = cross_prob # 交叉概率
self.pmuta_prob = pmuta_prob # 变异概率
self.select_prob = select_prob # 选择概率
self.data = data # 城市的坐标数据
self.num = len(data) # 有多少个城市，对应多少个坐标，对应染色体的长度（我们的解叫做染色体）
"""
计算城市的距离，我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()
self.select_num = int(self.size_pop * self.select_prob)
# 通过选择概率确定子代的选择个数
"""
初始化子代和父代种群，两者相互交替
"""
self.parent = np.array([0] * self.size_pop * self.num).reshape(self.size_pop, self.num)
self.child = np.array([0] * self.select_num * self.num).reshape(self.select_num, self.num)
"""
负责计算每一个个体的（瞎蒙的解）最后需要多少距离
"""
self.fitness = np.zeros(self.size_pop)
self.best_fit = []
self.best_path = []
# 保存每一步的群体的最优路径和距离
def __matrix_dis(self):
"""
计算14个城市的距离，将这些距离用矩阵存起来
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def rand_parent(self):
"""
初始化种群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.size_pop):
np.random.shuffle(rand_ch)
self.parent[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def comp_fit(self, one_path):
"""
计算，咱们这个路径的长度，例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
输出我们的路径顺序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def Select(self):
"""
通过我们的这个计算的距离来计算出概率，也就是当前这些个体DNA也就瞎蒙的解
之后我们在通过概率去选择个体，放到child里面
:return:
"""
fit = 1. / (self.fitness) # 适应度函数
cumsum_fit = np.cumsum(fit)
pick = cumsum_fit[-1] / self.select_num * (np.random.rand() + np.array(range(self.select_num)))
i, j = 0, 0
index = []
while i < self.size_pop and j < self.select_num:
if cumsum_fit[i] >= pick[j]:
index.append(i)
j += 1
else:
i += 1
self.child = self.parent[index, :]
def Cross(self):
"""
模仿DNA交叉嘛，就是交换两个瞎蒙的解的部分的解例如
A-B-C-D
C-D-A-B
我们选几个交叉例如这样
A-D-C-B
1,3号交换了位置，当然这里注意可不能重复啊
:return:
"""
if self.select_num % 2 == 0:
num = range(0, self.select_num, 2)
else:
num = range(0, self.select_num - 1, 2)
for i in num:
if self.cross_prob >= np.random.rand():
self.child[i, :], self.child[i + 1, :] = self.intercross(self.child[i, :],
self.child[i + 1, :])
def intercross(self, ind_a, ind_b):
"""
这个是我们两两交叉的具体实现
:param ind_a:
:param ind_b:
:return:
"""
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
ind_a1 = ind_a.copy()
ind_b1 = ind_b.copy()
for i in range(left, right + 1):
ind_a2 = ind_a.copy()
ind_b2 = ind_b.copy()
ind_a[i] = ind_b1[i]
ind_b[i] = ind_a1[i]
x = np.argwhere(ind_a == ind_a[i])
y = np.argwhere(ind_b == ind_b[i])
if len(x) == 2:
ind_a[x[x != i]] = ind_a2[i]
if len(y) == 2:
ind_b[y[y != i]] = ind_b2[i]
return ind_a, ind_b
def Mutation(self):
"""
之后是变异模块，这个就是按照某个概率，去替换瞎蒙的解里面的其中几个元素。
:return:
"""
for i in range(self.select_num):
if np.random.rand() <= self.cross_prob:
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
self.child[i, [r1, r2]] = self.child[i, [r2, r1]]
def Reverse(self):
"""
近化逆转，就是说下一次瞎蒙的解如果没有更好的话就不进入下一代，同时也是随机选择一个部分的
我们不是一次性全部替换
:return:
"""
for i in range(self.select_num):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
sel = self.child[i, :].copy()
sel[left:right + 1] = self.child[i, left:right + 1][::-1]
if self.comp_fit(sel) < self.comp_fit(self.child[i, :]):
self.child[i, :] = sel
def Born(self):
"""
替换，子代变成新的父代
:return:
"""
index = np.argsort(self.fitness)[::-1]
self.parent[index[:self.select_num], :] = self.child
def main(data):
Path_short = Gena_TSP(data) # 根据位置坐标，生成一个遗传算法类
Path_short.rand_parent() # 初始化父类
## 绘制初始化的路径图
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.parent[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色体的路程: ' + str(Path_short.fitness[0]))
# 循环迭代遗传过程
for i in range(Path_short.maxgen):
Path_short.Select() # 选择子代
Path_short.Cross() # 交叉
Path_short.Mutation() # 变异
Path_short.Reverse() # 进化逆转
Path_short.Born() # 子代插入
# 重新计算新群体的距离值
for j in range(Path_short.size_pop):
Path_short.fitness[j] = Path_short.comp_fit(Path_short.parent[j, :])
index = Path_short.fitness.argmin()
if (i + 1) % 50 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[index]))
print('第' + str(i + 1) + '步后的最优路径:')
Path_short.out_path(Path_short.parent[index, :]) # 显示每一步的最优路径
# 存储每一步的最优路径及距离
Path_short.best_fit.append(Path_short.fitness[index])
Path_short.best_path.append(Path_short.parent[index, :])
return Path_short # 返回遗传算法结果类
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
main(data)运行结果
ok,我们来看看运行的结果：
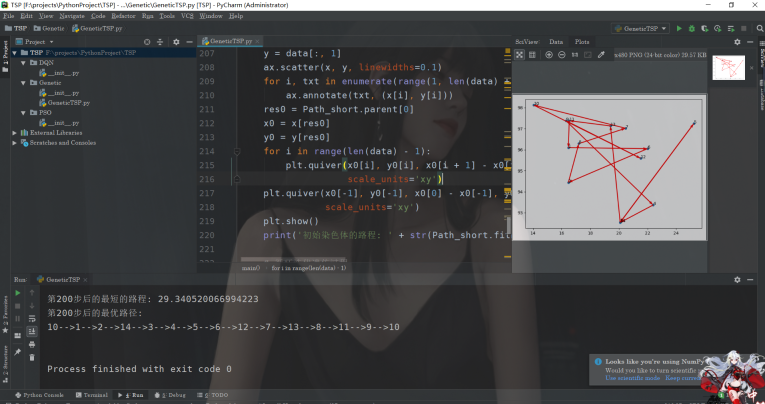
以上是如何利用Python實現遺傳演算法解決旅行商問題（TSP）？的詳細內容。更多資訊請關注PHP中文網其他相關文章！