超越核方法的量子機器學習，量子學習模型的統一框架

基於參數化量子電路的機器學習演算法是近期在吵雜的量子電腦上應用的主要候選者。在這個方向上，已經引入並廣泛研究了各種類型的量子機器學習模型。然而，我們對這些模型如何相互比較以及與經典模型進行比較的理解仍然有限。

近日，來自奧地利因斯布魯克大學的研究團隊確定了一個建設性框架，該框架捕獲所有基於參數化量子電路的標準模型：線性量子模型。

研究人員展示了使用量子資訊理論中的工具如何將資料重新上傳電路有效地映射到量子希爾伯特空間中線性模型的更簡單圖像中。此外，根據量子位元數和需要學習的資料量來分析這些模型的實驗相關資源需求。基於經典機器學習的最新結果，證明線性量子模型必須使用比資料重新上傳模型多得多的量子位元才能解決某些學習任務，而核方法還需要多得多的資料點。研究結果提供了對量子機器學習模型的更全面的了解，以及對不同模型與 NISQ 限制的兼容性的見解。

研究以「Quantum machine learning beyond kernel methods」為題，於2023 年1 月31 日發佈在《Nature Communications# 》上。

論文連結：https: //www.nature.com/articles/s41467-023-36159-y

在當前吵雜的中級量子(NISQ) 時代，已經提出了一些方法來建立與輕微的硬體限制相容的有用量子演算法。大多數這些方法都涉及量子電路 Ansatz 的規範，以經典方式最佳化以解決特定的計算任務。除了化學中的變分量子特徵求解器和量子近似優化演算法的變體之外，基於這種參數化量子電路的機器學習方法是產生量子優勢的最有希望的實際應用之一。

核方法（kernel methods）是一類模式辨識的演算法。其目的是找出並學習一組資料中的相互的關係。核方法是解決非線性模式分析問題的一種有效途徑，其核心思想是：首先，透過某種非線性映射將原始資料嵌入到合適的高維特徵空間；然後，利用通用的線性學習器在這個新的空間中分析和處理模式。

先前的工作透過利用一些量子模型和經典機器學習的核方法之間的聯繫，在這個方向上取得了長足的進步。許多量子模型確實是透過在高維希爾伯特空間中編碼數據，並僅使用在此特徵空間中評估的內積來對數據的屬性進行建模來運行。這也是核子方法的工作原理。

基於這種相似性，給定的量子編碼可用於定義兩種類型的模型：(a) 明確量子模型，其中編碼資料點根據指定其標籤的變分可觀測值進行測量；或(b) 隱式核模型，其中編碼資料點的加權內積用於分配標籤。在量子機器學習文獻中，許多重點都放在隱式模型上。

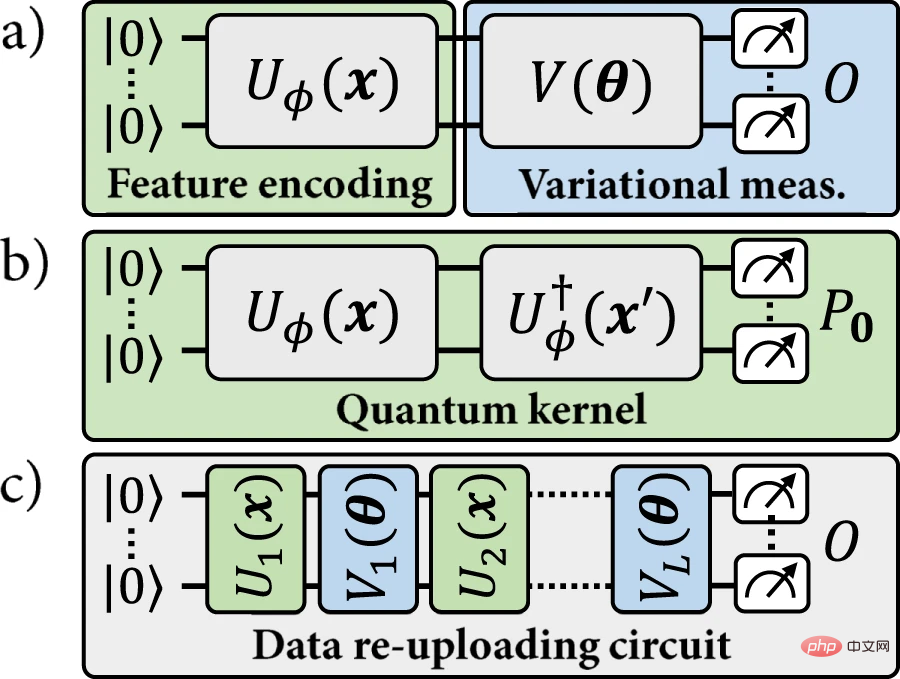
#圖 1：這項工作中研究的量子機器學習模型。 （資料來源：論文）

最近，所謂的資料重新上傳（data re-uploading）模型取得了進展。資料重新上傳模型可以看作是顯式模型的推廣。然而，這種概括也打破了與隱式模型的對應關係，因為給定的資料點 x 不再對應於固定的編碼點 ρ(x)。資料重新上傳模型比顯式模型嚴格更通用，它們與核心模型範例不相容。到目前為止，在核方法的保證下，是否可以從資料重新上傳模型中獲得一些優勢仍然是一個懸而未決的問題。

在這項工作中，研究人員引入了一個用於顯式、隱式和資料重新上傳量子模型的統一框架。

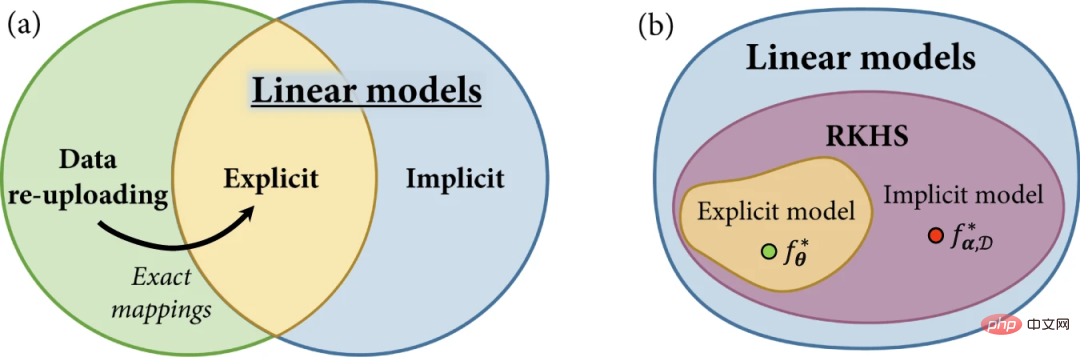
#圖 2：量子機器學習中的模型族。 （資料來源：論文）

量子學習模型的統一框架

#首先回顧線性量子模型的概念，並根據量子特徵空間中的定義線性模型解釋顯式和隱式模型。然後，展示了資料重新上傳模型，並展示了儘管被定義為顯式模型的推廣，但它們也可以透過更大的希爾伯特空間中的線性模型來實現。

線性量子模型

下圖給出了一個說明性結構，以直觀地說明如何實現從資料重新上傳到明確模型的映射。

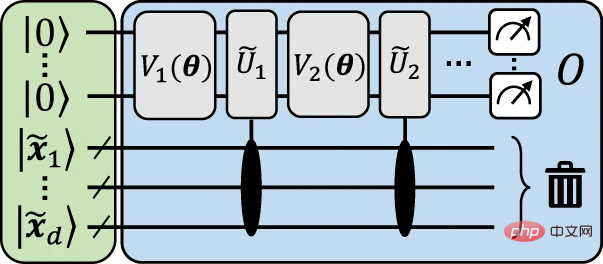
#圖 3：近似於資料重新上傳電路的說明性明確模型。 （資料來源：論文）

這個結構背後的整體想法是將輸入資料x 編碼為輔助量子位元，達到有限精度，然後可以重複使用它來使用與資料無關的單一體來近似資料編碼閘。

現在轉向主要結構，導致資料重新上傳和顯式模型之間的精確映射。在這裡，依賴與前面結構相似的思想，在輔助量子位元上對輸入資料進行編碼，然後使用資料獨立操作在工作量子位元上實現編碼閘。這裡的區別在於，使用門傳送（ gate-teleportation）技術，一種基於測量的量子計算，直接在輔助量子位上實現編碼門，並在需要時將它們傳送回（通過糾纏測量）到工作量子位上。

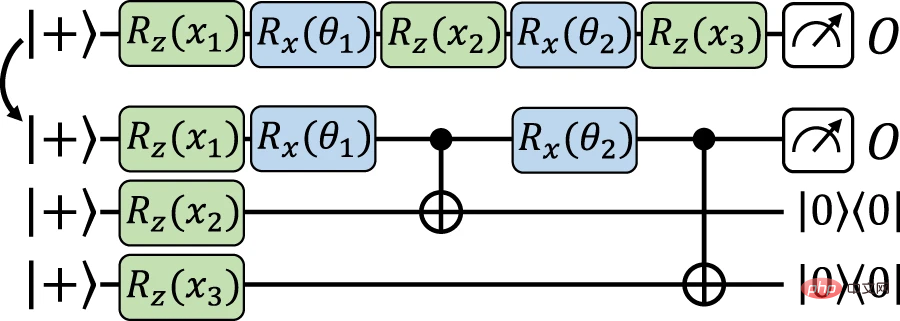
#圖4：使用閘隱形傳態從資料重新上傳模型到等效明確模型的精確映射。 （資料來源：論文）

研究人員證明了線性量子模型不僅可以描述顯式和隱式模型，還可以描述資料重新上傳電路。更具體地說，任何假設類別的資料重新上傳模型都可以映射到等效類別的顯式模型，即具有受限可觀察量族的線性模型。

接著，研究人員更嚴格地分析了顯式和資料重新上傳模型相對於隱式模型的優勢。在例子中，透過量子位元數和實現非平凡預期損失所需的訓練集大小來量化量子模型解決學習任務的效率。關注的學習任務是學習奇偶函數。

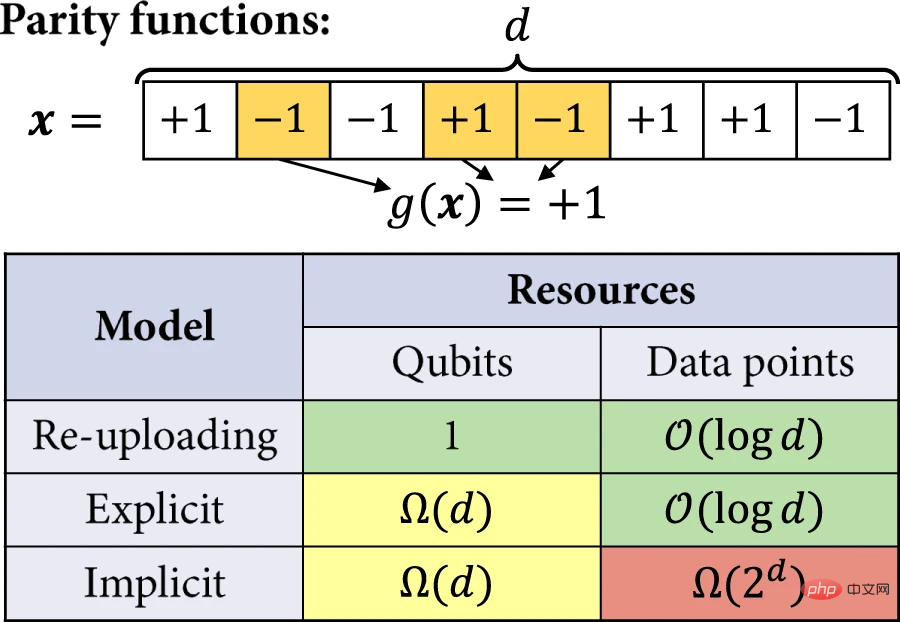
#圖 5：學習分離。 （資料來源：論文）

超越核方法的量子優勢

#量子機器學習的一個主要挑戰是，表明這項工作中討論的量子方法可以實現優於（標準）經典方法的學習優勢。

在這方面的研究中，Google量子人工智慧的Huang 等人（

######################################### ############https://www.php.cn/link/4dfd2a142d36707f8043c40ce0746761################）建議研究目標函數本身由（顯式）量子模型產生的學習任務。 ######

與 Huang 等人類似，研究人員使用 fashion-MNIST 資料集的輸入資料進行回歸任務，每個範例都是 28x28 的灰階影像。

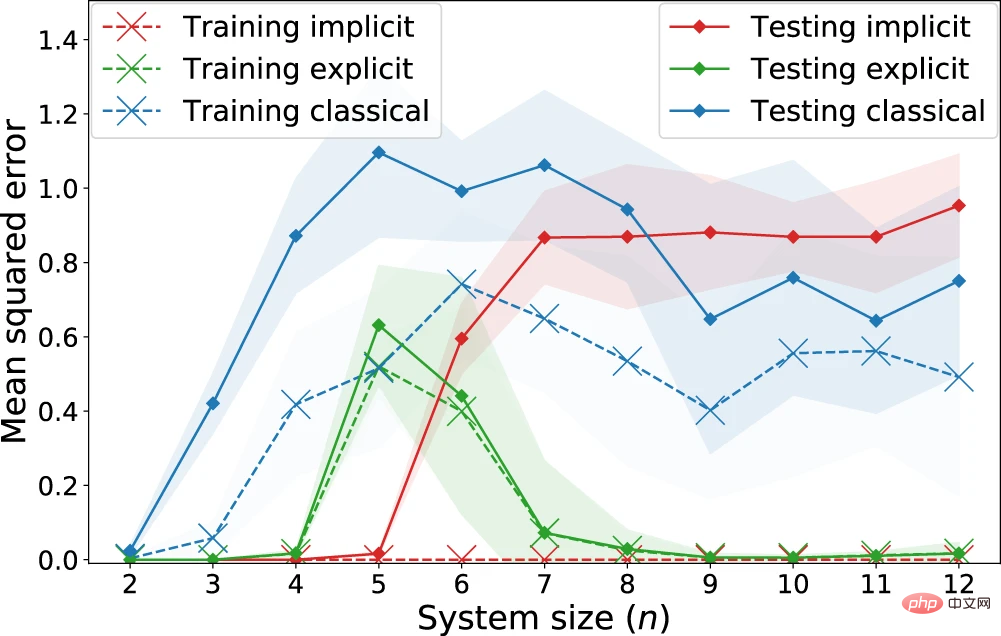
#圖6：顯式、隱式和經典模型在「量子客製」學習任務上的回歸性能。 （資料來源：論文）

觀察到：隱式模型系統地實現比顯式模型更低的訓練損失。特別是對於非正則化損失，隱式模型實現了 0 的訓練損失。另一方面，關於代表預期損失的測試損失，從 n = 7 量子位元開始的明顯分離，其中經典模型開始與隱式模型具有競爭性能，而顯式模型明顯勝過他們兩個。這表明，不應僅通過將經典模型與量子核方法進行比較來評估量子優勢的存在，因為顯式（或數據重新上傳）模型也可以隱藏更好的學習性能。

這些結果讓我們對量子機器學習領域有了更全面的了解，並拓寬了我們對模型類型的看法，以便在 NISQ 機制中實現實際的學習優勢。

研究人員認為證明不同量子模型之間存在指數學習分離的學習任務是基於奇偶函數的，這在機器學習中不是一個實際感興趣的概念類別。然而，下限結果也可以擴展到其他具有大維度概念類別（即由許多正交函數組成）的學習任務。

量子核方法必然需要許多與該維度成線性比例的資料點，而正如我們在結果中所展示的那樣，資料重新上傳電路的靈活性以及顯式模型的有限表達能力以節省大量資源。探索這些模型如何以及何時可以針對手邊的機器學習任務進行客製化仍然是一個有趣的研究方向。

以上是超越核方法的量子機器學習，量子學習模型的統一框架的詳細內容。更多資訊請關注PHP中文網其他相關文章！