Java如何實現的圖的遍歷
- 王林轉載
- 2023-05-05 16:43:061166瀏覽
1.圖的遍歷
從圖中某一頂點出發訪問圖中其餘頂點,且每個頂點僅被訪問一次
##圖的遍歷有兩種深度優先遍歷DFS、廣度優先遍歷BFS2.深度優先遍歷深度優先遍歷以深度為優先進行遍歷,簡單來說就是每次走到底。類似於二元樹的前序遍歷思路:1.以某一個頂點為起點進行深度優先遍歷,並標記該頂點已訪問2.以該頂點為起點選取任一路徑一直遍歷到底,並標記訪問過的頂點3.第2步遍歷到底後回退到上一個頂點,重複第2步4.遍歷所有頂點結束根據遍歷思路可知,這是一個遞歸的過程,其實DFS與回溯基本上相同。 遍歷: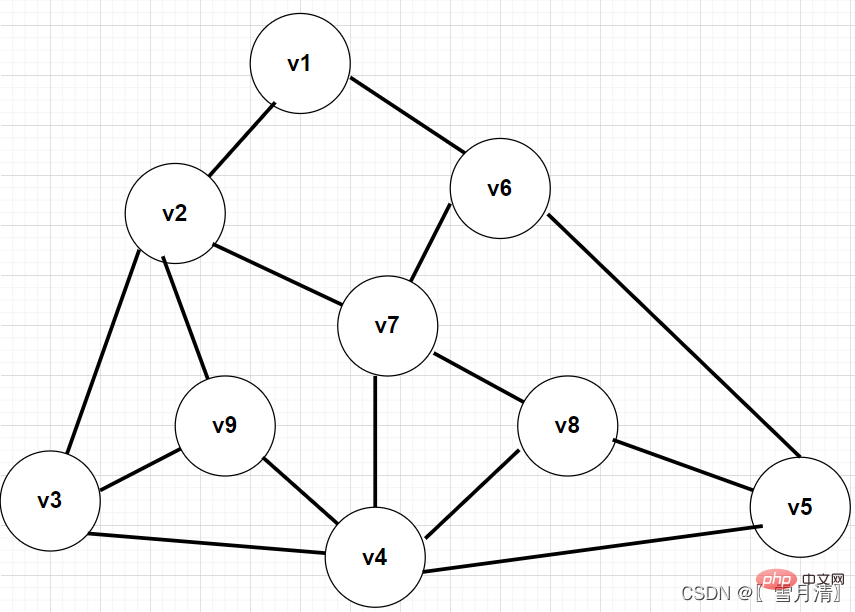
static void dfs(int[][] graph,int idx,boolean[]visit) {
int len = graph.length;
//访问过
if(visit[idx]) return;
//访问该顶点
System.out.println("V"+idx);
//标志顶点
visit[idx] = true;
for(int i = 1;i < len;i++) {
//访问该顶点相连的所有边
if(graph[idx][i] == 1) {
//递归进行dfs遍历
dfs(graph, i, visit);
}
}
}遍歷結果:
V1V2V3V4V5V6V7
V8
V9
建立圖的程式碼:public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
//顶点数 以1开始
int n = scanner.nextInt();
int[][] graph = new int[n+1][n+1];
//边数
int m = scanner.nextInt();
for(int i = 1;i <= m;i++) {
int v1 = scanner.nextInt();
int v2 = scanner.nextInt();
graph[v1][v2] = 1;
graph[v2][v1] = 1;
}
//标记数组 false表示未访问过
boolean[] visit = new boolean[n+1];
dfs(graph, 1, visit);
}3.利用DFS判斷有向圖是否存在環想法:遍歷某一個頂點時,如果除了上一個頂點之外,還存在其他相連頂點被訪問過,則必然存在環 //默认无环
static boolean flag = false;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
//顶点数 以1开始
int n = scanner.nextInt();
int[][] graph = new int[n+1][n+1];
//边数
int m = scanner.nextInt();
for(int i = 1;i <= m;i++) {
int v1 = scanner.nextInt();
int v2 = scanner.nextInt();
graph[v1][v2] = 1;
}
//标记数组 true为访问过
boolean[] visit = new boolean[n+1];
dfs(graph, 1, visit,1);
if(flag)
System.out.println("有环");
}
static void dfs(int[][] graph,int idx,boolean[]visit,int parent) {
int len = graph.length;
System.out.println("V"+idx);
//标记顶点
visit[idx] = true;
for(int i = 1;i < len;i++) {
//访问该顶点相连的所有边
if(graph[idx][i] == 1) {
if( !visit[i] ) {
dfs(graph, i, visit,idx);
}
else if(idx != i) {
flag = true;
}
}
}
}
#注意:是有向圖判斷是否存在環,無向圖判斷是否存在環無意義,因為任兩個存在路徑的頂點都可以是環
4.廣度優先遍歷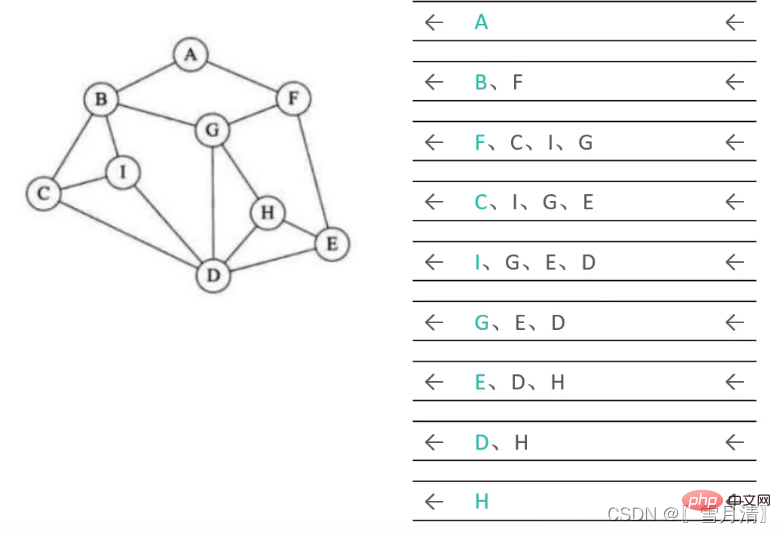 #廣度優先遍歷是以廣度(寬度)為優先進行遍歷。類似二元樹的層序遍歷
#廣度優先遍歷是以廣度(寬度)為優先進行遍歷。類似二元樹的層序遍歷
想法:
1.以某一個頂點為起點進行廣度優先遍歷,並標記該頂點已訪問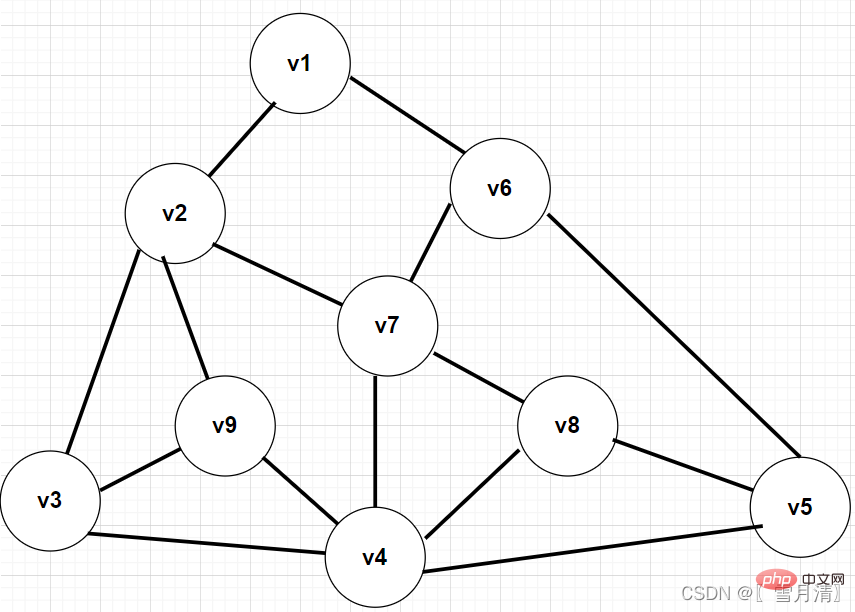
######## ######以此圖為例,採用鄰接矩陣的方式建立圖,進行BFS遍歷###透過佇列來輔助遍歷,隊列出隊順序即為廣度優先遍歷結果
遍歷
static void bfs(int[][] graph) {
int len = graph.length;
//标记数组 false表示未访问过
boolean[] visit = new boolean[len];
//辅助队列
Queue<Integer> queue = new LinkedList<>();
queue.offer(1);
visit[1] = true;
while(!queue.isEmpty()) {
int num = queue.poll();
System.out.println("V"+num);
//遍历该顶点所有相连顶点
for(int i = 1;i < len;i++) {
//相连并且没有被访问过
if(graph[num][i] == 1 && !visit[i]) {
queue.offer(i);
visit[i] = true;
}
}
}
}###遍歷結果:#########V1######V2 ######V6######V3######V7######V9######V5######V4######V8# ########建立圖表的程式碼###public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
//顶点数 以1开始
int n = scanner.nextInt();
int[][] graph = new int[n+1][n+1];
//边数
int m = scanner.nextInt();
for(int i = 1;i <= m;i++) {
int v1 = scanner.nextInt();
int v2 = scanner.nextInt();
graph[v1][v2] = 1;
graph[v2][v1] = 1;
}
bfs(graph);
}以上是Java如何實現的圖的遍歷的詳細內容。更多資訊請關注PHP中文網其他相關文章!
陳述:
本文轉載於:yisu.com。如有侵權,請聯絡admin@php.cn刪除
上一篇:Java實作二元樹的程式碼怎麼寫下一篇:Java實作二元樹的程式碼怎麼寫

