量子計算與人工智慧有什麼關係

經過數十年的研究，人工智慧 (AI) 正在成為主要的行業趨勢之一。從與Alexa 和Siri 的對話，到Waymo(Google)和特斯拉的自動駕駛汽車，OpenAI 的GPT-3 像人類一樣寫作散文，以及DeepMind(Google)的AlphaZero 擊敗人類國際圍棋大師，人工智慧現在已經足夠成熟了。解決現實生活中的問題，而且通常比人類更快更好。

在科技業的其他地方，一些有遠見的人正在努力開發量子計算機，這些計算機試圖利用量子物理學的特性來比當今的計算機更快地執行計算。

在這一點上，很多人可能想知道：量子計算與人工智慧到底有什麼關係?

演算法複雜性是隱藏的敵人

演算法複雜性是一個有點晦澀的數學概念，它將AI 研究人員和量子計算先驅所做的工作聯繫在一起。

計算複雜度理論是一個橫跨數學和電腦科學的領域，專注於根據資源使用情況對計算問題進行分類，例如空間(記憶體)和時間。本質上，計算問題是可以由計算機依照演算法中定義的數學步驟機械地解決的任務。

例如，考慮對清單中的數字進行排序的問題。一種可能的演算法，稱為“選擇排序”，包括從列表的未排序部分(最初是全部)重複找到最小元素(按升序)並將其放在開頭。該演算法有效地維護原始列表中的兩個子列表，因為它正在運行：已經排序的部分和剩餘的未排序部分。在這個過程經過幾次之後，結果是一個從小到大的排序清單。就時間複雜度而言，這用 N 2的複雜度來表示，其中 N 表示清單中元素的大小或數量。數學家提出了更有效率但更複雜的排序演算法，例如“Cube Sort”或“Tim Sort”，這兩種演算法的複雜度都是 N x log(N)。對於今天的電腦來說，對包含 100 個元素的清單進行排序是一項簡單的任務，但對包含十億筆記錄的清單進行排序可能就不那麼簡單了。因此，時間複雜度(或演算法中與輸入問題大小相關的步驟數)非常重要。

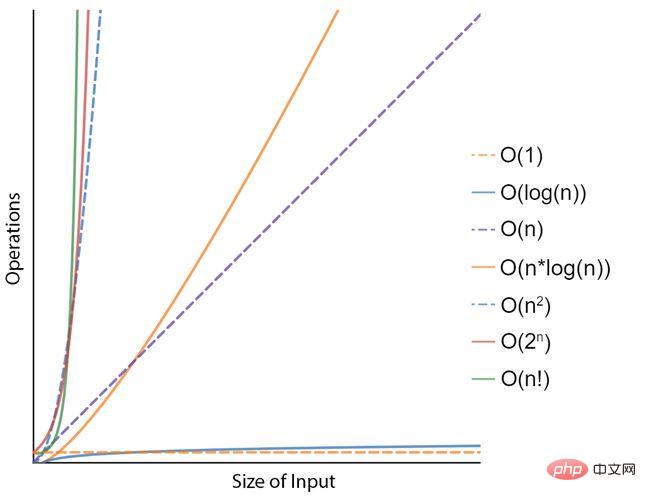
為了更快地解決問題，可以使用更快的計算機，或者找到需要更少操作的更有效演算法，這就是較低時間複雜度的含義。但是，很明顯，對於指數複雜度的問題(例如 N 2或 2 N)，數學對您不利，並且對於較大的問題規模，僅使用更快的計算機是不現實的。而這恰恰是人工智慧領域的情況。

人工智慧是一個需要解決的高度複雜的問題

首先，我們將了解當今人工智慧 (AI) 系統使用的人工神經網路的運算複雜性。這些數學模型的靈感來自構成動物大腦的生物神經網路。他們透過查看許多範例“學習”識別或分類輸入資料。它們是互連節點或神經元的集合，結合激活函數，該函數根據「輸入層」中呈現的數據和互連中的權重確定輸出。

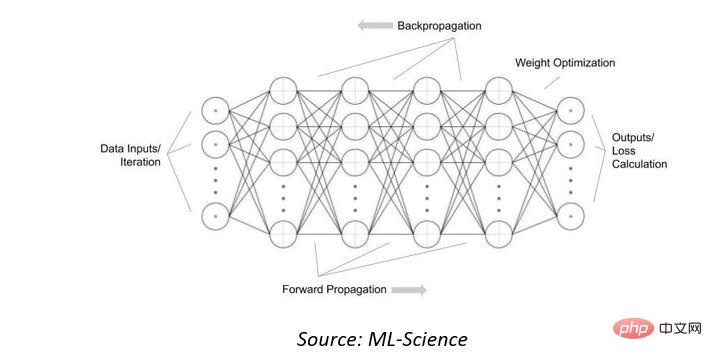
為了調整互連中的權重以使“輸出”有用或正確，可以透過暴露於許多資料範例和“反向傳播”輸出損失來“訓練”網路。

對於具有N個輸入、M個隱藏層的神經網絡，其中第i 個隱藏層包含m i個隱藏神經元和k個輸出神經元，調整所有神經元權重的演算法(稱為反向傳播演算法)將具有時間複雜度的：

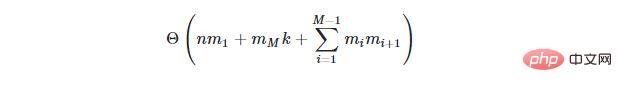
綜上所述，流行的OpenAI 的GPT-3 模型已經能夠以與人類相當的流暢度編寫原始散文，具有1750 億個參數(或神經元)。這個人工智慧模型擁有數十億的M，目前需要幾個月的時間來訓練，即使在大型雲端資料中心使用強大的伺服器電腦也是如此。此外，人工智慧模型的規模將繼續增長，因此隨著時間的推移情況會變得更糟。

量子運算來拯救?

量子電腦是使用量子物理特性(特別是疊加和糾纏)來儲存資料和執行計算的機器。期望它們可以同時執行數十億個操作，從而為高度複雜的問題(包括人工智慧)提供非常實質的加速。

經典電腦以位元(「二進位數字」的縮寫)傳遞訊息，而量子電腦使用量子位元(「量子位元」的縮寫)。與經典位元一樣，量子位元最終必須以 1 或 0 的形式傳輸訊息，但其特殊之處在於它們可以同時表示 1 和 0。一個量子位元被認為具有機率分佈，例如，它有 70% 的可能性是 1，而 30% 的可能性是 0。這就是量子計算機的特別之處。

量子電腦利用了量子力學中的兩個基本特性：疊加和糾纏。

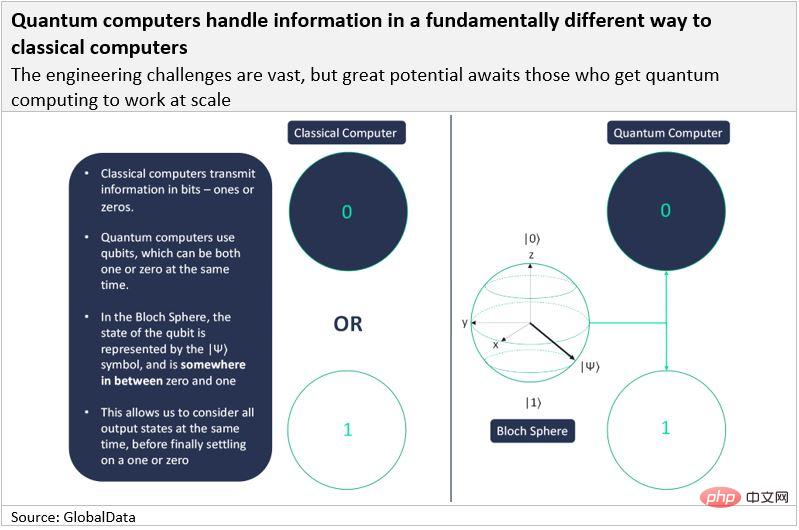
當量子位元同時為 1 和 0 時，稱它為疊加態。疊加是系統同時處於多個狀態並且在測量時僅假定單一狀態時的條件的總稱。如果我們假設一枚硬幣是一個量子物體，那麼當硬幣被翻轉時，就會產生疊加：硬幣只有正面或反面的機率。一旦硬幣落地，我們就進行了測量，我們知道硬幣是正面還是反面。同樣，只有當我們測量電子的自旋(類似於硬幣落地)時，我們才能知道電子處於什麼狀態以及它是 1 還是 0。

疊加態的量子粒子只有在我們擁有多個粒子時才有用。這將我們帶到了量子力學的第二個基本原理：糾纏。兩個(或多個)糾纏在一起的粒子無法單獨描述，它們的性質完全依賴彼此。因此，糾纏的量子位元可以相互影響。一個量子位元的機率分佈(一個或零)取決於系統中所有其他量子位元的機率分佈。

正因為如此，在系統中加入每個新的量子位元都會使電腦可以分析的狀態數量增加一倍。計算機能力的這種指數級增長與經典計算形成鮮明對比，經典計算僅隨每個新位線性擴展。

理論上，糾纏的量子位元可以同時執行數十億次操作。很明顯，這種能力將為任何複雜度在 N 2、2 N或 N N範圍內的演算法提供顯著的加速。

為量子驅動的人工智慧做好準備

由於量子運算的巨大潛力，雖然硬體團隊繼續致力於使這些系統成為現實(迄今為止最大的是IBM 的127-Qubit Eagle 系統)，但軟體研究人員已經在研究可以利用這種「同時計算」的新演算法' 能力，在密碼學、化學、材料科學、系統優化和機器學習/人工智慧等領域。相信 Shor 的因式分解量子演算法將提供比經典電腦更高的指數加速，這對目前的密碼演算法構成風險。

最有趣的是，人們相信量子線性代數將提供多項式加速，這將大大提高我們人工神經網路的效能。 Google推出了TensorFlow Quantum，這是一個用於量子機器學習的軟體框架，它允許對混合量子經典機器學習模型進行快速原型設計。同樣是量子計算的領導者，IBM 最近宣布，它發現了量子機器學習的量子優勢的“數學證明”. 然而，儘管IBM 和Google 等公司是垂直整合的(因此同時開發了硬體系統和軟體演算法) ，但也有一群非常有趣的量子軟體新創公司，包括Zapata、Riverlane、1Qbit，以及在一定程度上, Quantinuum(自從Cambridge Quantum Computing 與Honeywell 合併並更名後，它不再是一家純粹的軟體公司)，僅舉幾例。

隨著量子硬體變得更加強大和量子機器學習演算法的完善，量子運算很可能會在人工智慧晶片市場上佔據重要份額。

以上是量子計算與人工智慧有什麼關係的詳細內容。更多資訊請關注PHP中文網其他相關文章！